Hello, I require assistance with a dynamics project that involves three questions to be solved using Matlab. However, I currently do not have access to Matlab software. Would you be able to help me by showing the working process and providing explanations for the solutions? Your help would be greatly appreciated. Thank you in advance.

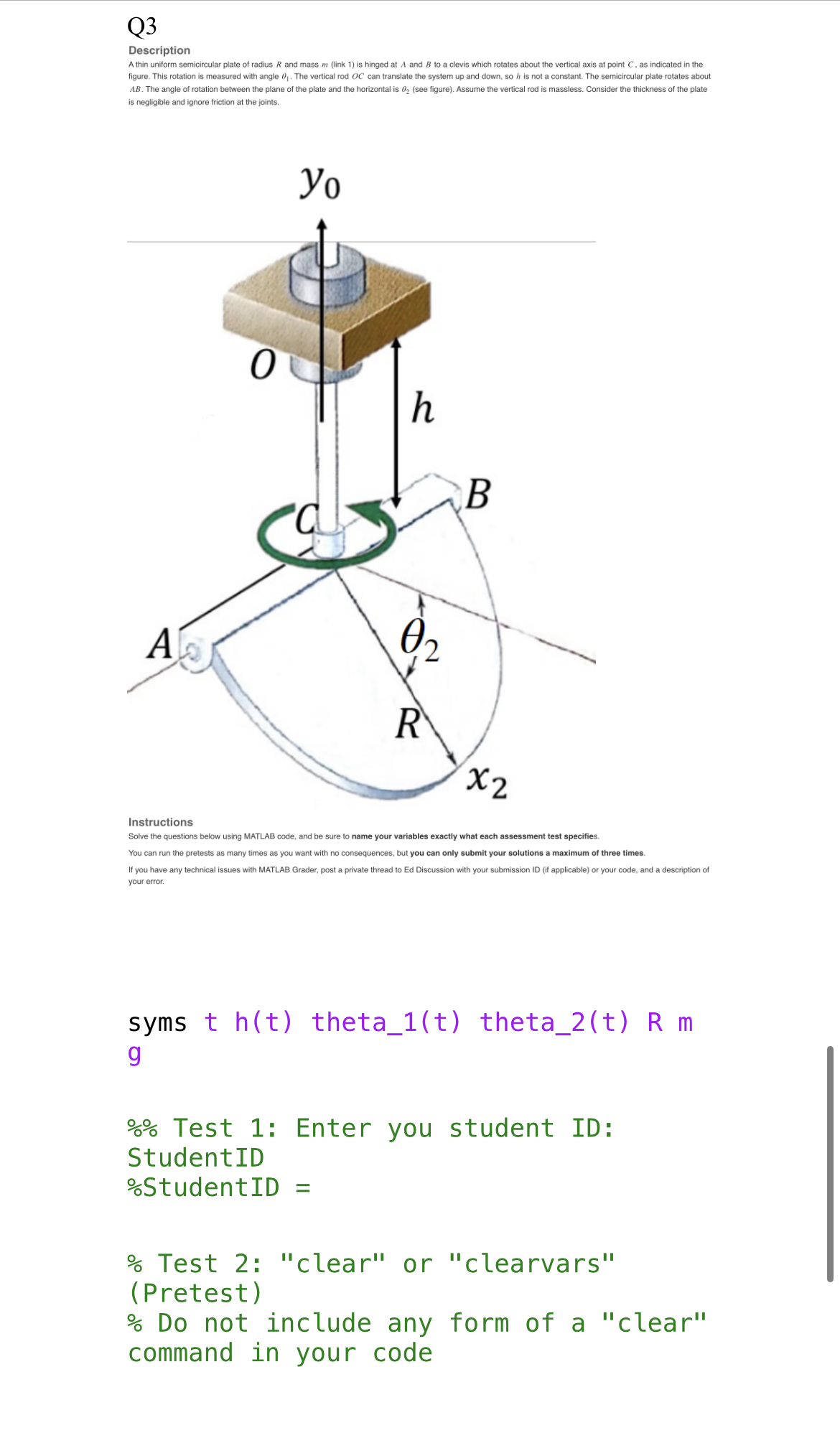
Dynamics Assignment 12 Done Q1: Description A motor spins a green disc which is connected at point B. The motor keeps the disc spinning at a constant rate 3 (theta_dot_3). The motor is supported by a horizontal grey rod (from point O to point A). The motor is capable of freely spinning about that rod, with its rotation measured by angle 2 (theta_2). The horizontal grey rod is connected to an orange vertical rod at point O, and it freely spins about that vertical rod, with its rotation measured by angle (theta_1). Point C is on the green disc, and it is pictured below at its lowest point, which is when axes z2 and o\\ o\\ Test 9: rBC_3 Find the position vector from point to point C in frame {3} DJ o\\ o\\ Test 10: r0C_2 Find the position vector from point 0 to point C in frame {2} o\\ o\\ Test 11: w1_1 (Pretest) Find the absolute angular velocity of the link that frame {1} is attached to, and express that vector in frame {1} o\\ o\\ Test 12: w21_2 (Pretest) 0 Find the angular velocity of the link that frame {2} is attached to, relative to the link that frame {1} is attached to, and express that vector in frame {2} \\ o\\ Q3 Description A thin uniform semicircular plate of radius R and mass m (link 1) is hinged at A and B to a clevis which rotates about the vertical axis at point C, as indicated in the figure. This rotation is measured with angle , . The vertical rod OC can translate the system up and down, so / is not a constant. The semicircular plate rotates about AB. The angle of rotation between the plane of the plate and the horizontal is 02 (see figure). Assume the vertical rod is massless. Consider the thickness of the plate s negligible and ignore friction at the joints. yo 0 h B a A LO R X2 Instructions Solve the questions below using MATLAB code, and be sure to name your variables exactly what each assessment test specifies. You can run the pretests as many times as you want with no consequences, but you can only submit your solutions a maximum of three times. If you have any technical issues with MATLAB Grader, post a private thread to Ed Discussion with your submission ID (if applicable) or your code, and a description of your error. syms t h(t) theta_1(t) theta_2(t) R m g %% Test 1: Enter you student ID: StudentID StudentID = " Test 2: "clear" or "clearvars" (Pretest) Do not include any form of a "clear" command in your code% Test 13: w32_3 % Find the angular velocity of the link that frame {3} is attached to, relative to the link that frame {2} is attached to, and express that vector in frame {3} Test 14: w3_3 Find the absolute angular velocity of the link that frame {3} is attached to, and express that vector in frame {3} o 'o o 'o % Test 15: r0C_dot_2 (Pretest) % Find the absolute linear velocity of point C in frame {2} Test 16: r0C_ddot_2 Find the absolute linear acceleration of point C in frame {2} o\\ o\\ % Test 17: w3_dot_2 % Find the absolute angular acceleration of the link that frame {3} is attached to, and express that vector in frame {2} % Test 3: R10 (Pretest) % Find the rotation matrix between the fixed frame and frame {1} o\\ R10 = % Test 4: R21 % Find the rotation matrix between the frames {1} and {2} o\\ R21 = % Test 5: C_to_centre_mass_2 (Pretest) % Find the position vector between the fixed point C and the centre of mass of the semicircular plate in frame {2} % C_to_centre_mass_2 = % Test 6: ang_vel_plate_2 % Find the absolute angular velocity of the plate in frame {2} o\\ ang_vel_plate_2 = Test 6: lin_acc_plate_2 Find the absolute linear acceleration of the plate in frame {2} o\\ o\\ % lin_acc_plate_2 = Instructions Solve the questions below using MATLAB code, and be sure to name your variables exactly what each assessment test specifies. You can run the pretests as many times as you want with no consequences, but you can only submit your solutions a maximum of three tunes If you have any technical issues with MATLAB Grader, post a private thread to Ed Discussion with your submission ID (if applicable) or your code, and a description of your error. References: Image source: Meriam, Kraige - Engineering Mechanics Dynamics. syms t theta_1(t) theta_2(t) theta_dot_3 L_1 L_2 L_3 rho %% Test 1: Enter you student ID: StudentID %StudentID = % Test 2: \"clear\" or \"clearvars\" (Pretest) % Do not include any form of a \"clear\" command in your code Test 3: R18 (Pretest) Find the rotation matrix that brings vector from frame {0} into frame {1} o\\ o\\ OJ Test 4: R21 (Pretest) Find the rotation matrix that brings vector from frame {1} into frame {2} o\\ o\\ (1) Test 5: R32 Find the rotation matrix that brings vector from frame {2} into frame {3} o\\ o\\ DJ Test 4: R21 Find the rotation matrix from frame {1} to the frame moving with the rectangular plate. o\\ o\\ % Test 5: cyl_to_sty_2 (Pretest) % Find the position vector from the centre of cylinder 83' to the centre of mass of the stylus in frame {2} % Test 6: pos_E_to_sty_2 % Find the position vector from point E to the centre of mass of the stylus in frame {2} Test 7: ang_vel_plate_DE_2 (Pretest) Find the angular velocity of the rectangular plate relative to component DE in frame {2} o\\ o\\ Test 8: ang_vel_sty_2 Find the absolute angular velocity of the stylus in frame {2} o\\ o\\ % Test 9: lin_vel_sty_1 (Pretest) % Find the absolute linear velocity of the centre of mass of the stylus in frame {1} Test 10: lin_acc_sty_D_2 0 Find the linear acceleration of the centre of mass of the stylus relative to point D in frame {2} \\ o\\ % Test 11: lin_acc_sty_2 % Find the absolute linear acceleration of the centre of mass of the stylus in frame {2} Q2 Description The position of the stylus tip A is controlled by the robot shown. A Force F, (not shown) keeps the stylus velocity at constant value is relative to the cylinder BB'. You may assume that intially, the centre of mass of the stylus (G) is at point C. Arm CD rotates about component DE, as shown in the picture. The entire robot rotates about the x, direction at a constant rate wj , controlled by a moment : (not shown). Assumptions of the problem: Link 1: Arm CD is a homogeneous rectangular thin plate of width a and mass m) . . The hollow cylinder BB' is massless. . Link 2: the stylus is a homogeneous thin rod of length 26 and mass my. Friction is negligible. Other dimensions are shown in the picture. yo W 1 CI h h * XO 2d L Instructions Solve the questions below using MATLAB code, and be sure to name your variables exactly what each assessment test specifies. You can run the pretests as many times as you want with no cons ces, but you can only submit your solutions a maximum of three times. If you have any technical issues with MATLAB Grader, post a private thread to Ed Discussion with your submission ID (if applicable) or your code, and a description of syms t omega_1 theta_2(t ) d L h a u m_1 m 2 b % Test 1: Enter you student ID: StudentID StudentID = " Test 2: "clear" or "clearvars" (Pretest) Do not include any form of a "clear" command in your code % Test 3: R01 (Pretest) Find the rotation matrix from frame {1} to the the fixed