Answered step by step
Verified Expert Solution
Question
1 Approved Answer
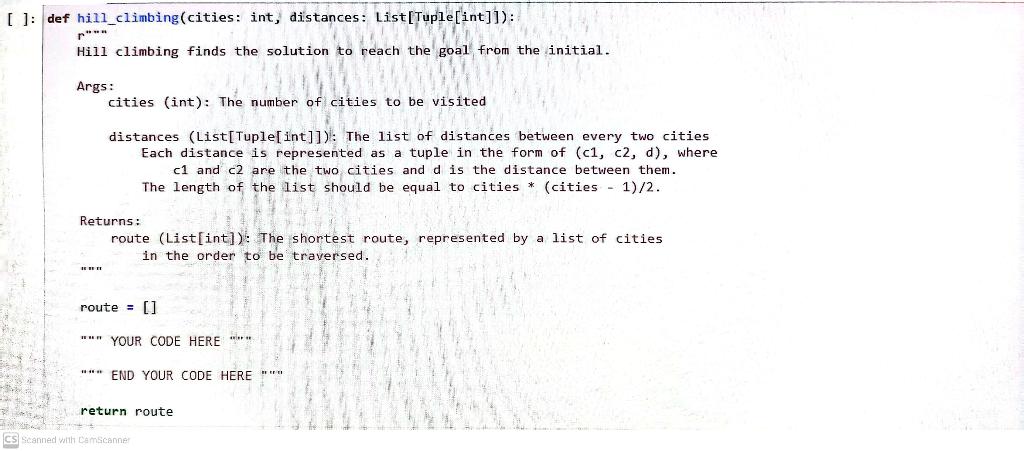
Hello, I'm stuck in this question. Can you help me to solve with code using Python. Pls make sure to run the test cases first.
Hello, I'm stuck in this question. Can you help me to solve with code using Python. Pls make sure to run the test cases first. Thank you so much for the help!!


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


