Hello, please help with the codes below using python programming (beginner level). The instructions are attached in the photos.

If they can be done within the next hour, that would be great. Thank you

Question 1:

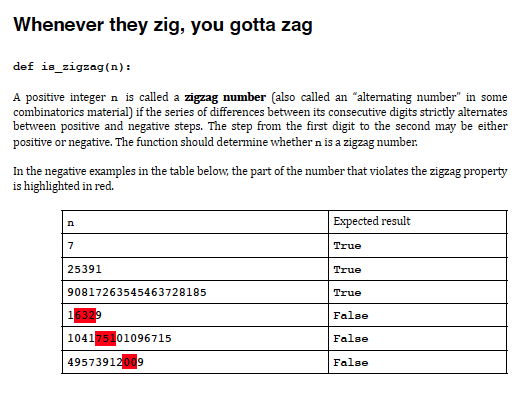
Chirality def is_left_handed (pipa) : Even though this has no effect on fairness, pips from one to six are not painted on dice any which way, but so that the pips on the opposite faces always add up to seven. (This convention makes it easier to tell when someone tries to use gaffed dice that leave out some spot values.) In each corner of the cube, one value from each pair of opposites 1-6, 2-5 and 3-4 meets two values from the other two pairs of opposites. The math works out correctly in for the 23 = 8 corners of the cube. This still leaves two possibilities how to paint these pips. Look at the corner shared by the faces 1, 2, and 3, and read these numbers clockwise around that corner starting from 1. If these three numbers read out as 1-2-3, that die is left-handed, and if they read out as 1-3-2, that die is right-handed. Analogous to a pair of shoes made separately for the left and right foot, left- and right-handed dice are in one sense identical, yet no matter how you twist and turn, you can't change either one to become indistinguishable from the other. (Well, at least not without taking that three-dimensional pancake "Through the Looking-Glass" by flipping it around in the fourth dimension!) The three numbers read around any other corner stamp the three numbers in the unseen opposite sides, and therefore determine the handedness of that entire die just as firmly. Given the three-tuple of pips around a corner read in clockwise order, determine whether that die is left-handed. There are only 23*3! = 8*6 = 48 possible pip combinations to test for but you should find and cheerily exploit as many of the ample symmetries in this problem as you can. pipe Expected result [1, 2, 3) True (1, 3, 5) True (5, 3, 1) False (6, 3, 2) True (6, 5, 4) False After solving that, imagine that our physical space had k dimensions, instead of merely just the familiar three. How would dice even be cast (in both senses of this word) in k dimensions? How would you generalize your function to find the chirality of an arbitrary k-dimensional die?Count growlers def count_growlers (animals) : Let the strings "cat' and 'dog' denote that kind of animal facing left, and 'tac' and 'god" denote that same kind of animal facing right. Each individual animal, regardless of its species, growls if it sees more dogs than cats to the direction that the animal is facing. Given a list of such animals, return the count of how many of these animals are growling. animals Expected result [ 'cat' , 'dog' ] [ 'god', 'cat', 'cat', 'tac', 'tac', 'dog' , 2 'cat' , 'god' ] [ 'dog', 'cat', 'dog', 'god', 'dog', 'god' , 11 'dog", 'god', 'dog', 'dog', 'god', 'god', 'cat', "dog', 'god', "cat' ", 'tac' ] [ 'god', 'tac", 'tac", 'tac', 'tac', 'dog', 0 'dog', 'tac', 'cat', 'dog', 'god', 'cat', 'dog', 'cat ', 'cat', 'tac' ] I admit that I was high as a kite when I originally thought up this problem, at least high enough to perceive the letter 't ' as a tail of a happy cat held up high, and the 'd' as the snout and stand-up ears of a curious dog, perhaps some kind of spitz or similar breed. (Yeah, good luck trying to un-see that now.) And yet for some reason, this problem is somehow more tricky than it would initially seem in a fair, predictable and just world, and does not seem to conveniently allow itself to be twisted into a clean and Pythonic solution. Readers are welcome to suggest their best solutions to the author, should they come up with nifty ways to solve this problem.Whenever they zig, you gotta zag def is_zigzag (n) : A positive integer n is called a zigzag number (also called an "alternating number" in some combinatorics material) if the series of differences between its consecutive digits strictly alternates between positive and negative steps. The step from the first digit to the second may be either positive or negative. The function should determine whether n is a zigzag number. In the negative examples in the table below, the part of the number that violates the zigzag property is highlighted in red. n Expected result 7 True 25391 True 90817263545463728185 True 16329 False 104175101096715 False 49573912009 FalseThe card that wins the trick def winning_card (cards, trump=None) : Playing cards are again represented as tuples of (rank, auit) as in the cardproblems . py lecture example program. In trick taking games such as whist or bridge, four players each play one card from their hand to the trick, committing to their play in clockwise order starting from the player who plays first into the trick. The winner of the trick is determined by the following rules: 1. If one or more cards of the trump suit have been played to the trick, the trick is won by the highest ranking trump card, regardless of the other cards played 2. If no trump cards have been played to the trick, the trick is won by the highest card of the suit of the first card played to the trick. Cards of any other suits, regardless of their rank, are powerless to win that trick. 3. Ace is the highest card in each suit. Note that the order in which the cards are played to the trick greatly affects the outcome of that trick, since the first card played in the trick determines which suits have the potential to win the trick in the first place. Return the winning card for the list of cards played to the trick. cards trump Expected result [( 'three' , 'spades'), ("ace', "diamonds" ), None ( 'jack , ( 'jack", "spades"), ( 'eight', "spades" ) ] "spades' } [('ace', 'diamonds"), ("ace' , "hearts'), ('ace", "clubs' ( 'two' "spades" ), ('two', "clubs' ) ] "cluba" [('two', 'clubs'), ("ace', 'diamonds"), ('ace' , None ( 'two' "hearts' ) ( 'ace", "spades" ) ] "cluba" )Expand positive integer intervals def expand_intervals (intervals) : An interval of consecutive positive integers can be succinctly described as a string that contains its first and last value, inclusive, separated by a minus sign. (This problem is intentionally restricted to positive integers so that there will be no ambiguity between the minus sign character used as a separator and an actual unary minus sign tacked in front of a digit sequence.) For example, the interval that contains the numbers 5, 6, 7, 8, 9 can be more concisely described as '5-9'. Multiple intervals can be described together by separating their descriptions with commas. An interval that contains only one value is given as only that value. Given a string that contains one or more such comma-separated interval descriptions, guaranteed to be given in sorted ascending order and never overlap with each other, create and return the list that contains all the integers contained inside these intervals. In solving this problem the same as any other problems, it is always better to not have to reinvent the wheel, but always check out first whether the string objects have useful methods to make your job easier. intervals Expected result [ ] [42] '4-6,10-12, 16 [4, 5, 6, 10, 11, 12, 16] '1,3-9,12-14,9999' [1, 3, 4, 5, 6, 7, 8, 9, 12, 13, 14, 9999]