Help in Python!!!

Using the WeightedGraphClient.py to solve the following problem. Use the problem data to change the vertices names and edges' weights accordingly. Modify the sample code output such that only the shortest path will be displayed, all other display is irrelevant and confusing. Please modify WeightedGraphClient.py having the appropriate modifications.

WeightedGraph.py

# Implement a weighted graph using classes for vertices and edges

from Heap import Heap import math

class Vertex(object): # A vertex in a graph def __init__(self, name): # Constructor: stores a vertex name self.name = name # Store the name

def __str__(self): # Summarize vertex in a string return ''.format(self.name)

class WeightedGraph(object): # A graph containing vertices and edges def __init__(self): # with weights. self._vertices = [] # A list/array of vertices self._adjMat = {} # Hash table maps vertex pairs to weight

def nVertices(self): # Get the number of graph vertices, i.e. return len(self._vertices) # the length of the vertices list

def nEdges(self): # Get the number of graph edges by return len(self._adjMat) // 2 # dividing the # of keys by 2

def __str__(self): # Summarize the graph in a string nVertices = self.nVertices() nEdges = self.nEdges() return ''.format( nVertices, 'ex' if nVertices == 1 else 'ices', nEdges, '' if nEdges == 1 else 's') def addVertex(self, vertex): # Add a new vertex to the graph self._vertices.append(vertex) # Place at end of vertex list

def validIndex(self, n): # Check that n is a valid vertex index if n

def addEdge( # Add edge of weight w between two self, A, B, w): # vertices A & B self.validIndex(A) # Check that vertex A is valid self.validIndex(B) # Check that vertex B is valid if A == B: # If vertices are the same raise ValueError # raise exception self._adjMat[A, B] = w # Add edge in one direction and self._adjMat[B, A] = w # the reverse direction

def hasEdge(self, A, B): # Check for edge between vertices A & B return ((A, B) in self._adjMat and # If vertex tuple in adjMat self._adjMat[A, B]

def edgeWeight(self, A, B): # Get edge weight between vertices self.validIndex(A) # Check that vertex A is valid self.validIndex(B) # Check that vertex B is valid return ( # If vertex tuple in adjMat, return self._adjMat[A, B] if (A, B) in self._adjMat else math.inf) # the weight stored there otherwise +

def vertices(self): # Generate sequence of all vertex indices return range(self.nVertices()) # Same as range up to nVertices def adjacentVertices( # Generate a sequence of vertex indices self, n): # that are adjacent to vertex n self.validIndex(n) # Check that vertex n is valid for j in self.vertices(): # Loop over all other vertices if j != n and self.hasEdge(n, j): # If other vertex connects yield j # via edge, yield other vertex index def adjacentUnvisitedVertices( # Generate a sequence of vertex self, n, # indices adjacent to vertex n that do visited, # not already show up in the visited list markVisits=True): # and mark visits in list, if requested for j in self.adjacentVertices(n): # Loop through adjacent if not visited[j]: # vertices, check visited if markVisits: # flag, and if unvisited, optionally visited[j] = True # mark the visit yield j # and yield the vertex index

def depthFirst( # Traverse the vertices in depth-first self, n): # order starting at vertex n self.validIndex(n) # Check that vertex n is valid visited = [False] * self.nVertices() # Nothing visited initially stack = Stack() # Start with an empty stack stack.push(n) # and push the starting vertex index on it visited[n] = True # Mark vertex n as visited yield (n, stack) # Yield initial vertex and initial path while not stack.isEmpty(): # Loop until nothing left on stack visit = stack.peek() # Top of stack is vertex being visited adj = None for j in self.adjacentUnvisitedVertices( # Loop over adjacent visit, visited): # vertices marking them as we visit them adj = j # Next vertex is first adjacent unvisited break # one, and the rest will be visited later if adj is not None: # If there's an adjacent unvisited vertex stack.push(adj) # Push it on stack and yield (adj, stack) # yield it with the path leading to it else: # Otherwise we're visiting a dead end so stack.pop() # pop the vertex off the stack

def breadthFirst( # Traverse the vertices in breadth-first self, n): # order starting at vertex n self.validIndex(n) # Check that vertex n is valid visited = [False] * self.nVertices() # Nothing visited initially queue = Queue() # Start with an empty queue and queue.insert(n) # insert the starting vertex index on it visited[n] = True # and mark starting vertex as visited while not queue.isEmpty(): # Loop until nothing left on queue visit = queue.remove() # Visit vertex at front of queue yield visit # Yield vertex to visit it for j in self.adjacentUnvisitedVertices( # Loop over adjacent visit, visited): # unvisited vertices queue.insert(j) # and insert them in the queue def minimumSpanningTree( # Compute a spanning tree minimizing edge self, n): # weight starting at vertex n self.validIndex(n) # Check that vertex n is valid tree = WeightedGraph() # Initial MST is an empty weighted graph nVerts = self.nVertices() # Number of vertices vMap = [None] * nVerts # Array to map vertex indices into MST edges = Heap( # Use heap for explored edges key=weight, # Store (A, B) vertex pair & weight in ) # each heap item, order by negative weight vMap[n] = 0 # Map start vertex into MST tree.addVertex(self.getVertex(n)) # Copy vertex n into MST while tree.nVertices()

def shortestPath( # Find shortest path between two vertices, self, start, end): # if it exists, as list of vertex indices visited = {} # Hash table of visited vertices costs = { # Hash of path costs to vertices including start: (0, start)} # their predecessor vertex while end not in visited: # Loop until we visit the end vertex nextVert, cost = None, math.inf # Look for next vertex for vertex in costs: # among unvisited vertices whose cost if (vertex not in visited and # to reach is the lowest costs[vertex][0] pathCost): # or old path costlier, costs[adj] = ( # update cost to reach vertex pathCost, nextVert) # via extended path path = [] # Build output path from end while end in visited: # Path only contains visited vertices path.append(end) # Append end vertex if end == start: # If we reached the start, break # we're done. Otherwise go to end = costs[end][1] # predecessor via lowest cost path return list(reversed(path)) # Return path from start to end def print(self, # Print all the graph's vertices and edges prefix=''): # Prefix each line with the given string print('{}{}'.format(prefix, self)) # Print summary form of graph for vertex in self.vertices(): # Loop over all vertex indices print('{}{}:'.format(prefix, vertex), # Print vertex index self.getVertex(vertex)) # and string form of vertex for k in range(vertex + 1, self.nVertices()): # Loop over if self.hasEdge(vertex, k): # higher vertex indices, if print(prefix, # there's an edge to it, print edge self._vertices[vertex].name, '', self._vertices[k].name, self.edgeWeight(vertex, k))

def weight(edge): return - edge[1]

class Stack(list): # Use list to define Stack class def push(self, item): self.append(item) # push == append def peek(self): return self[-1] # Last element is top of stack def isEmpty(self): return len(self) == 0

class Queue(list): def insert(self, j): self.append(j) def peek(self): return self[0] def remove(self): return self.pop(0) def isEmpty(self): return len(self) == 0

WeightedGraphClient.py

from WeightedGraph import *

import sys, random

# Default vertex names verts = ['Blum', 'Cerf', 'Dahl', 'Gray', 'Kay', 'Naur'] MSTedges = [ (0, 1, 31), (0, 2, 24), (1, 2, 35), (1, 3, 49), (1, 4, 38), (1, 5, 87), (2, 3, 41), (2, 4, 52), (3, 4, 25), (3, 5, 46), (4, 5, 43) ] SPedges = [ (0, 1, 22), (0, 2, 16), (1, 2, 29), (1, 3, 34), (1, 4, 26), (1, 5, 65), (2, 3, 28), (2, 4, 24), (3, 4, 25), (3, 5, 30), (4, 5, 36) ]

seed = 3.14159

if len(sys.argv) > 1: verts = sys.argv[1:] seed = hash(''.join(verts)) random.seed(seed) nVerts = len(verts)

if len(sys.argv) > 1: maxEdges = nVerts ** 2 // 4 MSTedges, SPedges = [], [] for edges in [MSTedges, SPedges]: print('Making edges for', 'minimum spanning tree' if edegs is MSTedges else 'shortest path') for i in range(maxEdges): j = random.randrange(nVerts - 1) k = random.randrange(j + 1, nVerts) weight = random.randrange(1, 100) if (j, k) in [(a, b) for a, b, _ in edges]: print('Skipping duplicate edge from', j, 'to', k) else: print('Adding edge from', j, 'to', k, 'with weight', weight) edges.append((j, k, weight))

graph = WeightedGraph() print('Initial weighted graph:', graph)

nVerts = len(verts) for vert in verts: graph.addVertex(Vertex(vert))

print('After adding', nVerts, 'vertices, weighted graph contains') graph.print()

for j, k, weight in MSTedges: graph.addEdge(j, k, weight) print('After adding minimum spanning tree edges, weighted graph contains') graph.print()

print('Checking some random potential edges') for i in range(10): j = random.randrange(nVerts - 1) k = random.randrange(j + 1, nVerts) print('Does weighted graph have edge from', j, graph.getVertex(j).name, 'to', k, graph.getVertex(k).name, '?', 'yes' if graph.hasEdge(j, k) else 'no', 'weight:', graph.edgeWeight(j, k))

for start in (0, nVerts - 1): print('Depth-first traversal of weighted graph starting at', start, ':') for visit, path in graph.depthFirst(start): print('Visiting', graph.getVertex(visit).name, 'via', path, '-'.join(graph.getVertex(j).name for j in path)) print('End depth-first traversal') print('Breadth-first traversal of weighted graph starting at', start, ':') for visit in graph.breadthFirst(start): print('Visiting', graph.getVertex(visit).name) print('End breadth-first traversal') print('Minimuum-spanning tree of weighted graph starting at', start, ':') graph.minimumSpanningTree(start).print() print(' Checking that bad indices cause exceptions') for j, k in ((0, 0), (-1, 0), (0, graph.nVertices())): try: print('Trying to create an edge from', j, 'to', k) graph.addEdge(j, k, 0) except IndexError as e: print('IndexError was raised') except ValueError as e: print('ValueError was raised') print('All index tests passed. ')

graph = WeightedGraph() for vert in [None, 'A']: if vert: graph.addVertex(Vertex(vert)) print('Minimuum-spanning tree of weighted graph', graph, 'starting at 0 is') try: graph.minimumSpanningTree(0).print() except Exception as e: print('minimumSpnningTree() raised exception:', e) print('All tests of minimum spanning tree on trivial graphs passed. ')

graph = WeightedGraph() nVerts = len(verts) for vert in verts: graph.addVertex(Vertex(vert))

for j, k, weight in SPedges: graph.addEdge(j, k, weight) print('After adding shortest path edges, weighted graph contains') graph.print()

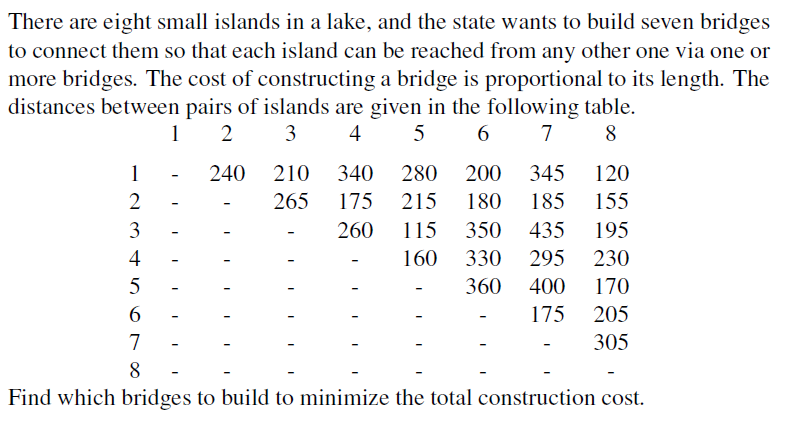
for end in (nVerts - 1, nVerts - 2): start = 0 shortest = graph.shortestPath(start, end) cost = 0 if len(shortest) There are eight small islands in a lake, and the state wants to build seven bridges to connect them so that each island can be reached from any other one via one or more bridges. The cost of constructing a bridge is proportional to its length. The distances between pairs of islands are given in the following table. Find which bridges to build to minimize the total construction cost