help me to solve this

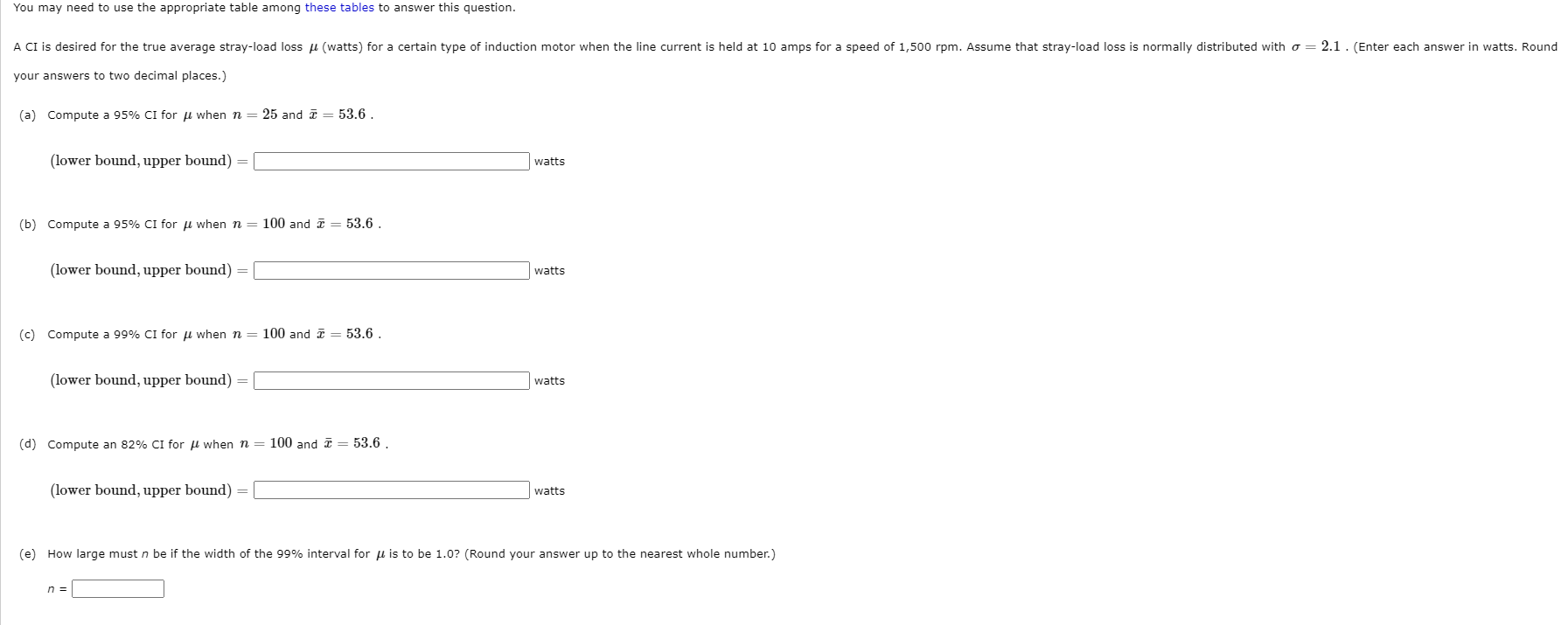
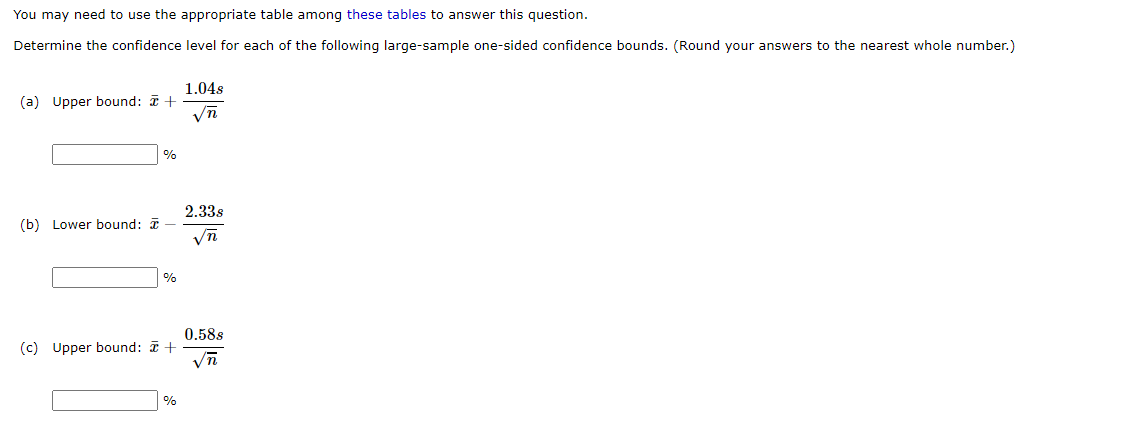
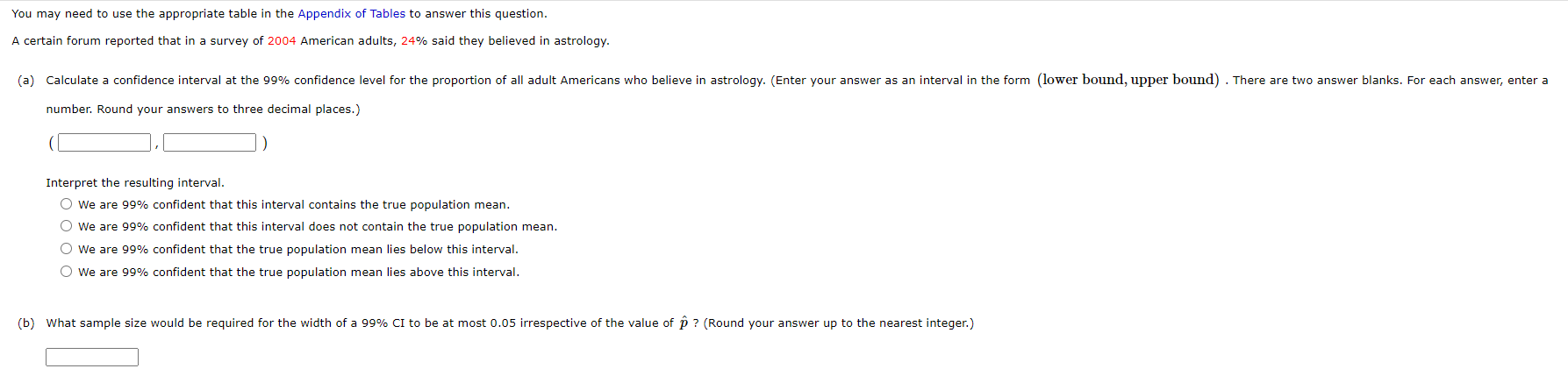
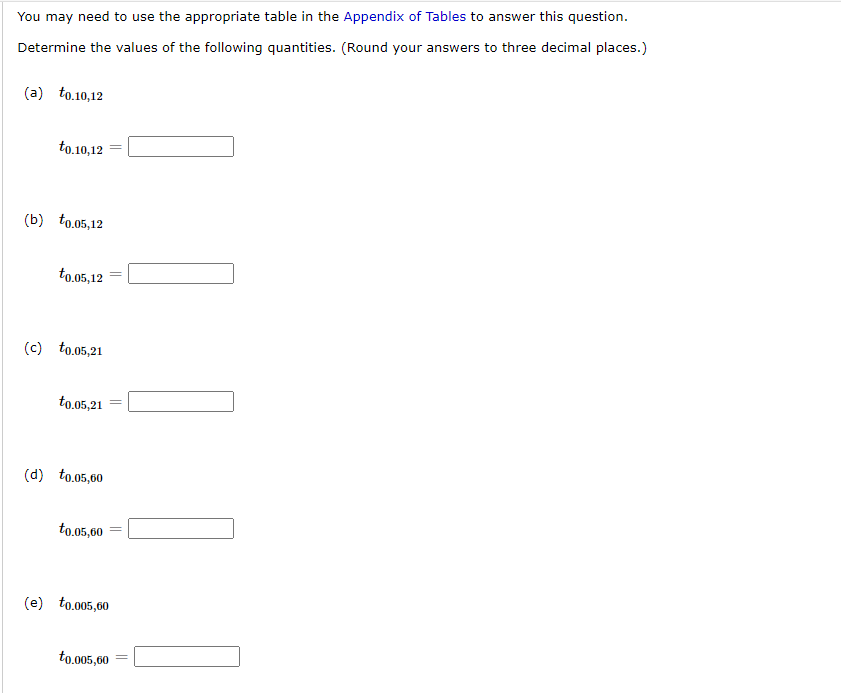
You may need to use the appropriate table among these tables to answer this question. Consider the next 1,000 90% CIs for / that a statistical consultant will obtain for various clients. Suppose the data sets on which the intervals are based are selected independently of one another. How many of these 1,000 intervals do you expect to capture the corresponding value of / ? expected number of intervals = intervals What is the probability that between 890 and 910 of these intervals contain the corresponding value of / ? [Hint: Let Y equal the number among the 1,000 intervals that contain / . What kind of random variable is Y?] (Round your answer to four decimal places.) probability =You may need to use the appropriate table among these tables to answer this question. The technology underlying hip replacements has changed as these operations have become more popular (over 250,000 in the United States in 2008). Starting in 2003, highly durable ceramic hips were marketed. Unfortunately, for too many patients the increased durability has been counterbalanced by an increased incidence of squeaking. An article reported that in one study of 157 individuals who received ceramic hips between 2003 and 2005, 8 of the hips developed squeaking. (a) Calculate a lower confidence bound at the 95% confidence level for the true proportion of such hips that develop squeaking. (Round your answer to three decimal places.) lower confidence bound = (b) Interpret the 95% confidence level used in (a). We are 95% confident that the true proportion of all such artificial hip recipients who experience squeaking is less than the lower bound. We are 95% confident that the true proportion of all such artificial hip recipients who experience squeaking is greater than the lower bound.\fA survey collects demographic, socioeconomic, dietary, and health-related information on an annual basis. Here is a sample of 20 observations on HDL cholesterol level (mg/dl) obtained from the survey (HDL is "good" cholesterol; the higher its value, the lower the risk for heart disease). 34 48 51 53 66 52 52 46 85 35 45 34 40 44 38 62 94 34 31 47 (a) Calculate a point estimate (in mg/dl) of the population mean HDL cholesterol level. mg/di (b) Making no assumptions about the shape of the population distribution, calculate a point estimate (in mg/dl) of the value that separates the largest 50% of HDL levels from the smallest 50%. mg/dl (c) Calculate a point estimate (in mg/dl) of the population standard deviation. (Round your answer to three decimal places.) mg/dl (d) An HDL level of at least 60 is considered desirable as it corresponds to a significantly lower risk of heart disease. Making no assumptions about the shape of the population distribution, estimate the proportion p of the population having an HDL level of at least 60.You mayr need to use the appropriate table among these tables to answer this question. Consider a normal population distribution with the value of (T known. 2.88:1 (a) What is the condence level for the interval i :l: ? (Round your answer to one decimal place.) :% _ 1.430 (b) What is the condence level for the interval 2 :: 1/ . ? (Round your answer to one decimal place.) E % (c) Consider the following CI formula. 0' 0' :+z x 3/71, of? 52.,\" x What value of 3G1\" in the CI formula results in a condence level of 99.?%? [Round your answer to two decimal places.) from = E (d) What value of an\" in the CI formula results in a condence level of ?l%? (Round your answer to two decimal places.) zap = S You may need to use the appropriate table among these tables to answer this question. A CI is desired for the true average stray-load loss / (watts) for a certain type of induction motor when the line current is held at 10 amps for a speed of 1,500 rpm. Assume that stray-load loss is normally distributed with o = 2.1 . (Enter each answer in watts. Round your answers to two decimal places.) (a) Compute a 95% CI for / when n = 25 and i = 53.6 . (lower bound, upper bound) = watts (b) Compute a 95% CI for / when n = 100 and a = 53.6. (lower bound, upper bound) watts (c) Compute a 99% CI for / when n = 100 and i = 53.6. (lower bound, upper bound) = watts (d) Compute an 82% CI for / when n = 100 and i = 53.6 . (lower bound, upper bound) =[ watts (e) How large must n be if the width of the 99% interval for / is to be 1.0? (Round your answer up to the nearest whole number.) n =You may need to use the appropriate table among these tables to answer this question. Determine the condence level for each of the following large-sample one-sided condence bounds. (Round your answers to the nearest whole number.) 1.043 (E (a) Upper bound: :7: + Eek 2.33s (b) Lower bound: i Eek 0.583 (E (c) Upper bound: :7: + :w5 You may need to use the appropriate table in the Appendix of Tables to answer this question. A certain forum reported that in a survey of 2004 American adults, 24% said they believed in astrology. (a) Calculate a confidence interval at the 99% confidence level for the proportion of all adult Americans who believe in astrology. (Enter your answer as an interval in the form (lower bound, upper bound) . There are two answer blanks. For each answer, enter a number. Round your answers to three decimal places.) Interpret the resulting interval. O We are 99% confident that this interval contains the true population mean. O We are 99% confident that this interval does not contain the true population mean. O We are 99% confident that the true population mean lies below this interval. O We are 99% confident that the true population mean lies above this interval. (b) What sample size would be required for the width of a 99% CI to be at most 0.05 irrespective of the value of p ? (Round your answer up to the nearest integer.)You may need to use the appropriate table in the Appendix ofTables to answer this question. Determine the values of the following quantities. (Round your answers to three decimal places.) {a} toms: mum = E {b} tones: tum: = E {C} 1511.05.21 imam = E {d} 1511.05.60 mum = E (9} inseam imam = E You may need to use the appropriate table among these tables to answer this question. Ultra high performance concrete (UHPC) is a relatively new construction material that is characterized by strong adhesive properties with other materials. The article "Adhesive Power of Ultra High Performance Concrete from a Thermodynamic Point of View" | described an investigation of the intermolecular forces for UHPC connected to various substrates. The following work of adhesion measurements (in ml/m) for UHPC specimens adhered to steel appeared in the article. 107.1 109.5 107.4 106.8 108. (a) Is it plausible that the given sample observations were selected from a normal distribution? O It's plausible that the distribution could be normal. O It's not plausible that the distribution could be normal. (b) Calculate a two-sided 95% confidence interval for the true average work of adhesion for UHPC adhered to steel. (Enter your answers in mJ/m . Enter your answer as an interval in the form (lower bound, upper bound) . There are two answer blanks. For each answer, enter a number. Round your answers to two decimal places.) ) mJ/m3 Does the interval suggest that 108 is a plausible value for the true average work of adhesion for UHPC adhered to steel? The interval suggests that 108 is a possible value for the true average O The interval doesn't suggest that 108 is a possible value for the true average. Does the interval suggest that 111 is a plausible value for the true average work of adhesion for UHPC adhered to steel? The interval suggests that 111 is a possible value for the true average. O The interval doesn't suggest that 111 is a possible value for the true average. (c) Predict the resulting work of adhesion value resulting from a single future replication of the experiment by calculating a 95% prediction interval. (Enter your answers in mJ/mu. Enter your answer as an interval in the form (lower bound, upper bound) . There are two answer blanks. For each answer, enter a number. Round your answers to two decimal places.) ) mJ/m3 Compare the width of this interval to the width of the CI from part (b). O The CI is wider than the PI. The two intervals are the same width. O The PI is wider than the CI. (d) Calculate an interval for which you can have a high degree of confidence that at least 95% of all UHPC specimens adhered to steel will have work of adhesion values between the limits of the interval. (Enter your answers in mJ/m . Enter your answer as an interval in the form (lower bound, upper bound) . There are two answer blanks. For each answer, enter a number. Round your answers to two decimal places.) 1) mJ/m3