Help me understand the following questions. This question is complete

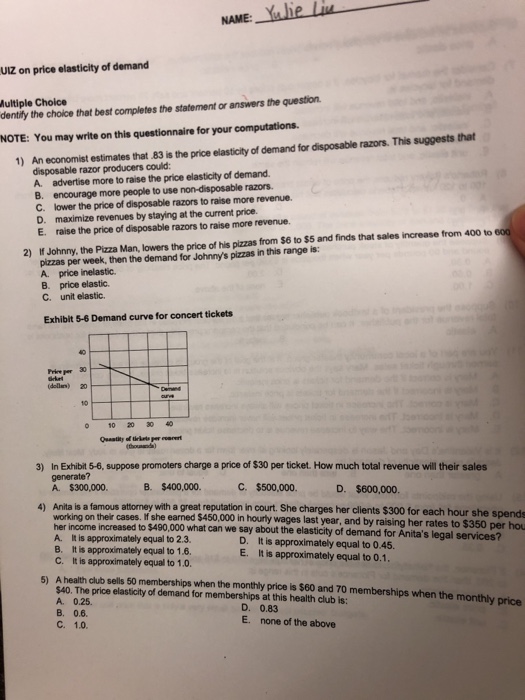
IS-LM Model (Based on Mankiw Ch. 12 #3). Use the information about the following economy to build the IS-LM model. a. The consumption function is given by C = 300 + 0.6(Y - ). The investment function is / = 700 - 80r. Government spending and taxes are both 500. Graph the IS curve for this economy. Be sure to label the x- and y-axes. b. The money demand function is (M/p) = Y - 200r. The money supply M is 3,000 and the price level P is 3. On the same graph as in part a.), graph the LM curve. c. Find the equilibrium interest rate r and the equilibrium level of income Y. Label the equilibrium values on your graph. d. Suppose that government spending is increased from 500 to 700. How does the IS curve shift? What are the new equilibrium interest rate and level of income? Show the shift and the new equilibrium on your graph. e. Suppose instead that the money supply is increased from 3,000 to 4,500. How does the LM curve shift? What are the new equilibrium and level of income? On a new graph, show the original IS and LM curves and then show the shift and the new equilibrium. f. With the initial values for monetary and fiscal policy, suppose that the price level rises from 3 to 5. What happens? What are the new equilibrium interest rate and level of income? On a new graph, show the original IS and LM curves and then show the shift and the new equilibrium. g. . For the initial values of monetary and fiscal policy, derive and graph an equation for the aggregate demand curve (Hint: Solve the IS and LM curves in terms of r. Then combine them and solve for Y in terms of P.). What happens to this aggregate demand curve if fiscal or monetary policy changes, as in parts d.) and e.) (simply state which direction the aggregate demand curve shifts in each case)?NAME: Yulie Live UIZ on price elasticity of demand Multiple Choice dentify the choice that best completes the statement or answers the question. NOTE: You may write on this questionnaire for your computations. 1) An economist estimates that .83 is the price elasticity of demand for disposable razors. This suggests that disposable razor producers could: A. advertise more to raise the price elasticity of demand. B. encourage more people to use non-disposable razors C. lower the price of disposable razors to raise more revenue. D. maximize revenues by staying at the current price. E. raise the price of disposable razors to raise more revenue. 2) If Johnny, the Pizza Man, lowers the price of his pizzas from $6 to $5 and finds that sales increase from 400 to 600 pizzas per week, then the demand for Johnny's pizzas in this range is: A. price inelastic. B. price elastic. C. unit elastic. Exhibit 5-6 Demand curve for concert tickets 30 are 10 Quantity of thebelo per coarm thou generate? 3) In Exhibit 5-6, suppose promoters charge a price of $30 per ticket. How much total revenue will their sales A. $300,000. B. $400,000. C. $500,000. D. $600,000. 4) Anita is a famous attorney with a great reputation in court. She charges her clients $300 for each hour she spend working on their cases. If she earned $450,000 in hourly wages last year, and by raising her rates to $350 per hou her income increased to $490,000 what can we say about the elasticity of demand for Anita's legal services? A. It is approximately equal to 2.3. B. It is approximately equal to 1.6. D. It is approximately equal to 0.45. C. It is approximately equal to 1.0. E. It is approximately equal to 0.1. A. 0.25. 5) A health club sells 50 memberships when the monthly price is $60 and 70 memberships when the monthly price $40. The price elasticity of demand for memberships at this health club is: B. 0.6. D. 0.83 C. 1.0. E. none of the above42. In class, we've discussed the fact that the baseline models we've constructed can be extended to incorporate more advanced techniques. Let's look at a specic extension that incorporates the concept of price discrimination. In particular, assume that a rm with constant marginal cost of $2 (and no xed cost) has two types of customers The rst type has a market demand of 01 (p) = 30 p. The second type is more price sensitive and has a market demand of D2 (p) = 30 2p. A. Assume the rm can only set a single price. For instance, when an individual shows up to purchase a good, the rm cannot determine which type of consumer she is. What is the maximal prot the rm can achieve. HINT: This is pretty much a standard market power model where you need to solve for the market demand, prot maximize, then determine if the rm would sell to each customer. B. Now, assume the rm can set a different price in each market. For instance, the rm can offer senior citizen discounts. If the rm prot maximizes in market 1 and also market 2, what prices will be set in each market? C. How much extra prot will the rm receive by price discriminating (i.e., setting a different price in each market)? 4. Consider a variant on the Aghion and Tirole (1997) model. Poppy, the principal, and Aiden, the agent, together can decide on implementing a new project, but both are unsure of which project is good and which is really bad. Given this, if no one is informed they will not do any project and both parties get zero. Both Poppy and Aiden can, however, put effort into discovering a good project. Poppy can put in effort E; this costs her effort cost - E' , but it gives her a probability of being informed of E. If Poppy gets her preferred project she will get a payoff of $1. For all other projects Poppy gets zero. Similarly, the agent Aiden can put in effort e at a cost of - e'; this gives Aiden a probability of being informed with probability e. If Aiden 2 gets his preferred project he gets $1. For all other projects he gets zero. Note also, that the probability that Poppy's preferred project is also Aiden's preferred project is a (this is the degree of congruence is a). It is also the case that a if Aiden chooses his preferred project that it will also be the preferred project of Poppy. (Note, in this question, we assume that a = [ from the standard model studied in class.) (a) Assume that Poppy has the legal right to decide (P-formal authority). If Poppy is uninformed she will ask the agent for a recommendation; if Aiden is informed he will recommend a project to implement. First consider the case when both Aiden and Poppy simultaneously choose their effort costs. Write out the utility or profit function for both Poppy and Aiden. Solve for the equilibrium level of E and e, and show that Poppy becomes perfectly informed (E = 1) and Aiden puts in zero effort in equilibrium (e = 0). Explain your result, possibly using a diagram of Poppy's marginal benefit and marginal cost curves. What is Poppy's expected profit? (b) Now consider the case when the agent Aiden has the formal decision making rights (Delegation or A-formal authority). In this case, if Aiden is informed he will decide on the project if he is informed; if not he will ask Poppy for a recommendation. Again calculate the equilibrium levels of E and e