Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Help please! 45% of the students failed in statistics, 35% in computer and 25% in both statistics and computer courses. A randomly selected student, a)
Help please!
45% of the students failed in statistics, 35% in computer and 25% in both statistics and computer courses. A randomly selected student, a) If it fails from the computer, the probability of failing the statistics, b) If it fails from statistics, the probability of failing from the computer, c) Find the probability of failing at least one of these two courses.
I have a 30 minutes to send. Please help me

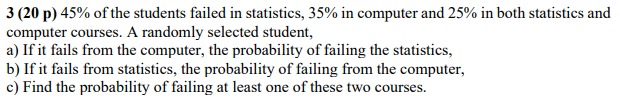


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


