Help please, this is what I have so far.

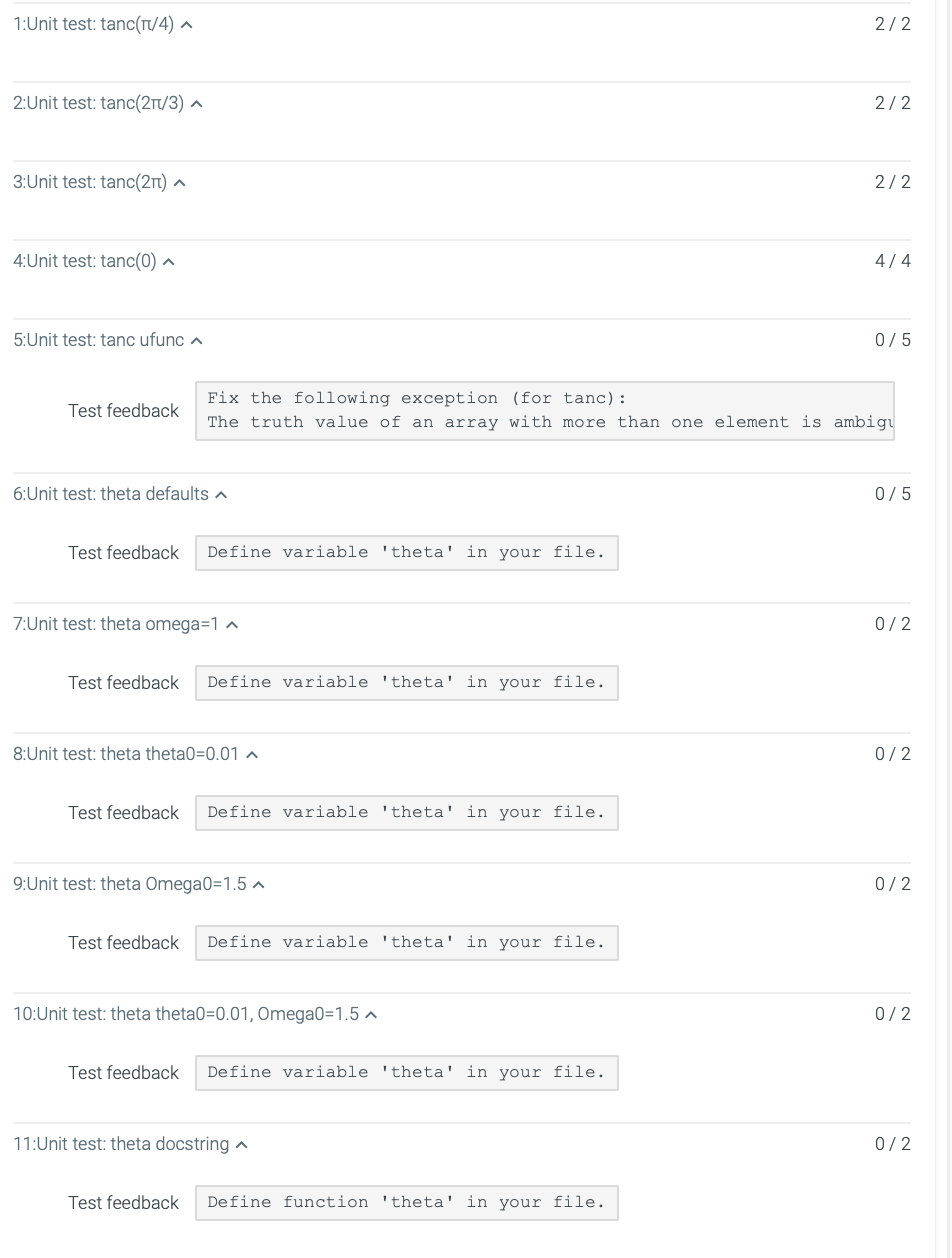
Solve the following problems. Use numpy and numpy arrays when possible. Problem 1: tanc function Define the function tancx:=xtanx as a Python function tanc(x). 1. Note that the function value at x=0 is well defined limx0tancx=1. Your function should take this into account. 2. Your function should behave like a numpy ufunc, i.e., it should be possible to use a numpy array as an argument and then it should return an array of the same size in which tanc() was applied element-wise. For example: >x=nppinparray([0,0.25,1]) >tanc(X) array([1.0,1.27323954e+00,3.89817183e17]) Note: Getting (2) to work is much harder than (1). Try to get (1) to work first (the initial tests only test scalar arguments). Problem 2: Harmonic pendulum trajectory The trajectory (t) (angle as a function of time) of the harmonic pendulum can be expressed as (t)A=Acos(t+)=02+(0)8=arctan(00/) It depends on the frequency and the initial conditions 0=(0) (initial angle) and 0=(0)=(0) (initial angular velocity). Write a Python function theta ( ) to compute the trajectory for given time points. The function must do the following: 1. takes an array t of times as mandatory argument; 2. takes the mandatory argument omega to set the frequency; 3. returns an array of the same size as t in which (t) was evaluated for each element in t; 4. contains a doc string that briefly explains the function and the arguments that it takes; 5. takes an optional argument theta 0 with default value /6; 6. takes an optional argument 0mega0 with default value 0 . 459736.3079258.qx3zqy7 \begin{tabular}{|l|l|} \begin{tabular}{|l|l} LAB & 18.3.1: Functions \\ ACTIVITY \end{tabular} \\ 1 \# add your code \\ 2 \# (only function definitions are tested) \\ 3 import math \\ 4 import numpy as np \\ 5 & \\ 6 def tanc(x): \\ 7 & if x=0: \\ 8 & tanc =(nptan(x)/x) \\ 9 & return tanc \\ 10 & else: \\ 11 & tanc =1.0 \\ 12 & return tanc \\ 13 & \end{tabular} 1:Unit test: tanc(/4) 2/2 2:Unit test: tanc(2/3) 2/2 3: Unit test: tanc(2) 2/2 4:Unit test: tanc(0) 4/4 5:Unit test: tanc ufunc 0/5 \begin{tabular}{l|l|} Test feedback & Fix the following exception (for tanc): \\ The truth value of an array with more than one element is ambigu \end{tabular} 6:Unit test: theta defaults 0/5 Test feedback 7:Unit test: theta omega =1 0/2 Test feedback 8:Unit test: theta theta0 =0.01 0/2 Test feedback 9:Unit test: theta Omega0 =1.5 0/2 Test feedback 10:Unit test: theta theta 0=0.01, Omega 0=1.5 ^ 0/2 Test feedback 11:Unit test: theta docstring 0/2 Test feedback