help solve 4

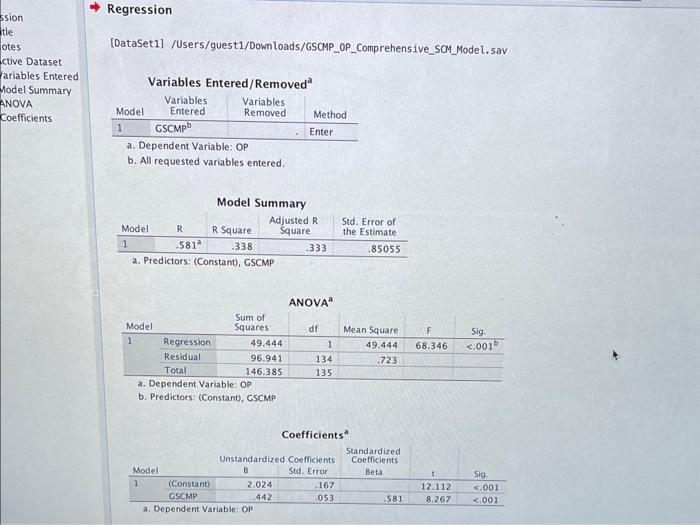
significance (,,ns) following the Beta value. Beta- .581R2.338 4. Interpret the results in the model answering the question: "Does GSCMP positively impact OP?" First interpret the Beta. Is it positive and significant at either the .01 or .05 level? Second, interpret the R2 value by moving the decimal to places to the right to turn it into a percentage. If the Beta is positive and significant, conclude that GSCMP does positively impact OP. Interpret the R2 percentage in this way: "The variation in GSCMP explains % of the variation in OP." Regression [DataSet1] /Users/guest1/Downloads/GSOMP_OP_Comprehensive_SCM_Model.sav ctive Dataset ariables Entered Model Summary ANOVA Coefficients Variables Entered/Removed a a. Dependent Variable: OP b. All requested variables entered. Model Summary b. Predictors: (Constant), CSCMP Coefficients a Significance levels in regression analysis. Consider the following SPSS output. Note that the standardized coefficient (beta) for the MO to JIT link is .278 with a computed significance level of .004 . Several folks incorrectly interpreted the significance level as .05 instead of 01 . Once again, here are the decision criteria for determining the significance level of a regression coefficient: 1. If the computed significance level is less than or equal to .01 , the significance level is .01 (**) 2. If the computed significance level is greater than .01 but less than or equal to .05 , the significance level is .05 (*) 3. If the computed significance level is greater than .05 , the coefficient is not significantly different from zero (not significant or ns) Now, take a look at the computed significance level of .004. Since .004 is less than .01 , the beta of .278 is significant at the .01 level. Let's try another example. Consider the following regression output. The computed significance level for the .036 beta is .725 . Since .725 is greater than .05 , the beta is not significant. The computed significance level for the .242 beta is .078 . Since .078 is greater than .05 , the beta is not significant. The computed significance level for the .379 beta is .002 . Since .002 is less than .01 , the beta is significant at the .01 level