Help solve for all parts
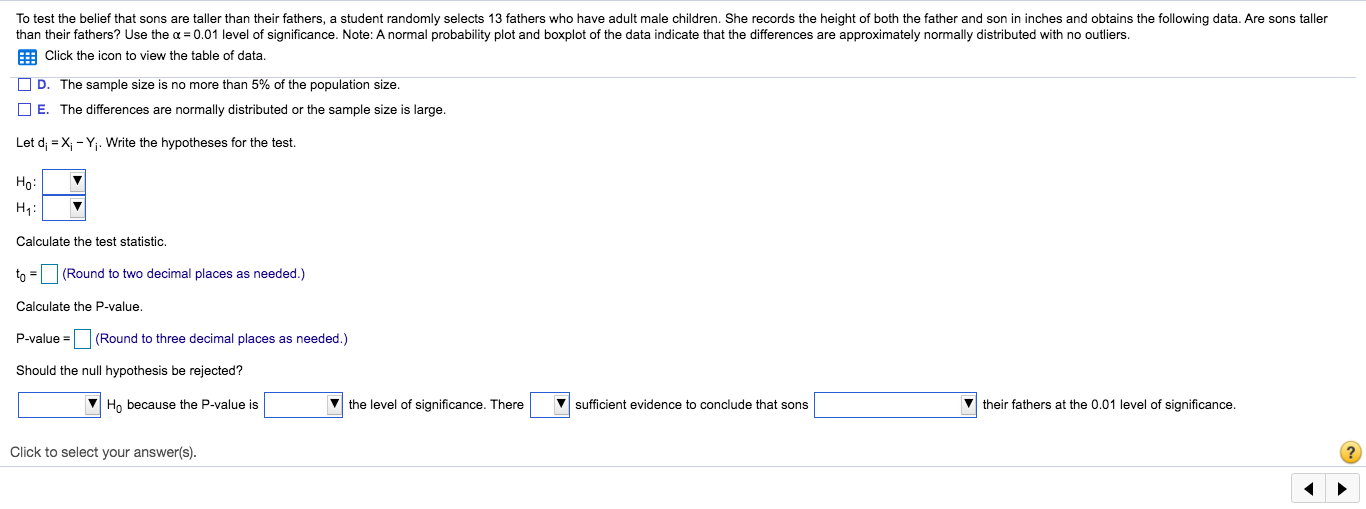
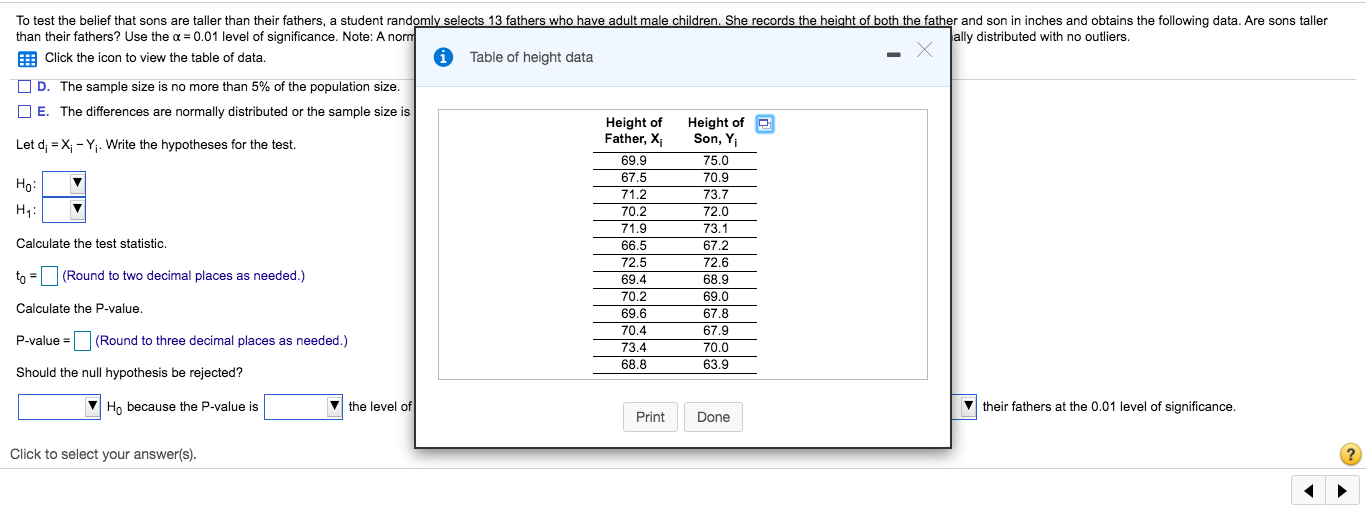
To test the belief that sons are taller than their fathers, a student randomly selects 13 fathers who have adult male children. She records the height of both the father and son in inches and obtains the following data. Are sons taller than their fathers? Use the a = 0.01 level of significance. Note: A normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers. Eff Click the icon to view the table of data. Which conditions must be met by the sample for this test? Select all that apply. A. The sampling method results in a dependent sample. B. The sampling method results in an independent sample. C. The sample size must be large. D. The sample size is no more than 5% of the population size. E. The differences are normally distributed or the sample size is large. Let dj = X; - Yj. Write the hypotheses for the test. Ho: H1 Calculate the test statistic. to =(Round to two decimal places as needed.) Click to select your answer(s). ?To test the belief that sons are taller than their fathers, a student randomly selects 13 fathers who have adult male children. She records the height of both the father and son in inches and obtains the following data. Are sons taller than their fathers? Use the a = 0.01 level of significance. Note: A normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers. Click the icon to view the table of data. D. The sample size is no more than 5% of the population size. E. The differences are normally distributed or the sample size is large. Let di = X; - Yj. Write the hypotheses for the test. Ho H1: Calculate the test statistic. to =(Round to two decimal places as needed.) Calculate the P-value. P-value = (Round to three decimal places as needed.) Should the null hypothesis be rejected? Ho because the P-value is the level of significance. There sufficient evidence to conclude that sons their fathers at the 0.01 level of significance. Click to select your answer(s). ?To test the belief that sons are taller than their fathers, a student randomly selects 13 fathers who have adult male children. She records the height of both the father and son in inches and obtains the following data. Are sons taller than their fathers? Use the a = 0.01 level of significance. Note: A nom ally distributed with no outliers. Click the icon to view the table of data. i Table of height data X D. The sample size is no more than 5% of the population size. WE. The differences are normally distributed or the sample size is Height of Height of Let dj = X; - Yj. Write the hypotheses for the test. Father, Xi Son, Y 69.9 75.0 Ha: 67.5 70.9 71.2 73.7 H1 70.2 72.0 71.9 73. Calculate the test statistic. 66.5 $7.2 to = (Round to two decimal places as needed.) 72.5 72.6 69.4 68.9 Calculate the P-value. 70.2 $9.0 69.6 67.8 P-value = (Round to three decimal places as needed.) 70.4 37. 73.4 70.0 Should the null hypothesis be rejected? 68.8 63.9 Ho because the P-value is the level of Print Done their fathers at the 0.01 level of significance. Click to select your answer(s).