Help with a and b! Please explain steps.

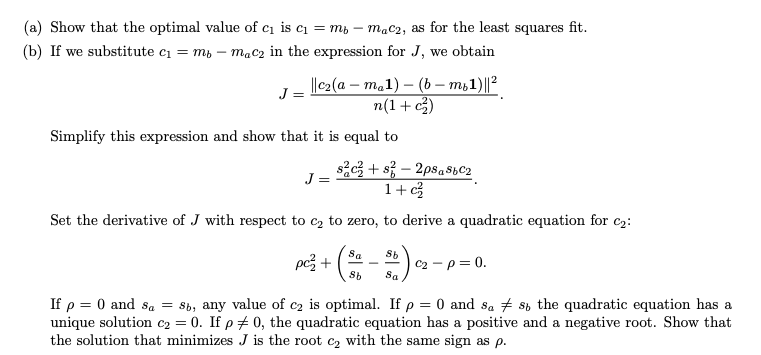
Orthogonal distance regression. We use the same notation as in exercise 1.7: a, b are non-constant n-vectors, with means ma, mb, standard deviations sa, Sb, and correlation coefficient p. y (ak, bk) y = ci + c22 For each point (ax, bk), the vertical deviation from the straight line defined by y=ci + c2x is given by ex = |c + c2ak bxl. The least squares regression method of the lecture minimizes the sum kez of the squared vertical deviations. The orthogonal (shortest) distance of (ak,bk) to the line is c + Cyan -bel V1 + c As an alternative to the least squares method, we can find the straight line that minimizes the sum of the squared orthogonal distances Ex d2. Define J ||411+cza 6|12 dhe n(1 + c) dki n n k=1 (a) Show that the optimal value of c is c = mb m,C2, as for the least squares fit. (b) If we substitute ci = mb - macy in the expression for J, we obtain J = ||c2(a - m 1) (6 - m 1) ||2 n(1+z) Simplify this expression and show that it is equal to szcz + s} - 2ps a $6C2 J= 1+c Set the derivative of J with respect to cz to zero, to derive a quadratic equation for cy: Sa pc + 02-p=0. Sb Sa If p = 0 and sa = Sb, any value of c2 is optimal. If p = 0 and sa 7 st the quadratic equation has a unique solution C2 = 0. If p #0, the quadratic equation has a positive and a negative root. Show that the solution that minimizes J is the root c, with the same sign as p