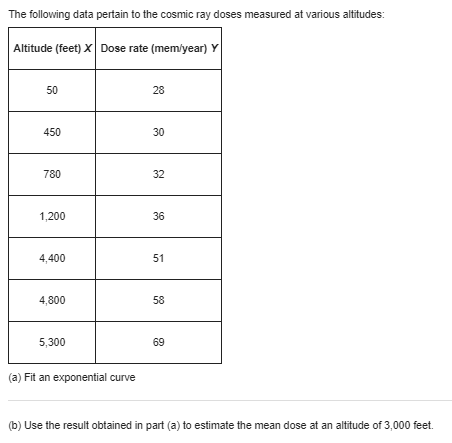





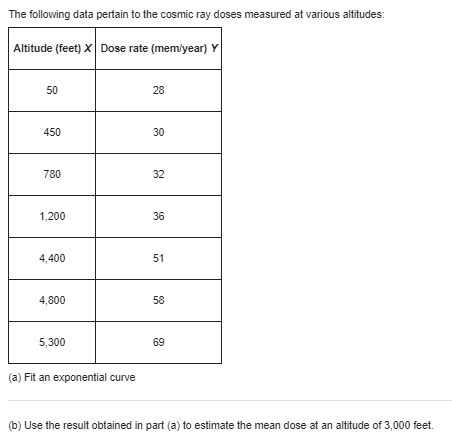
help with assignment questions:-
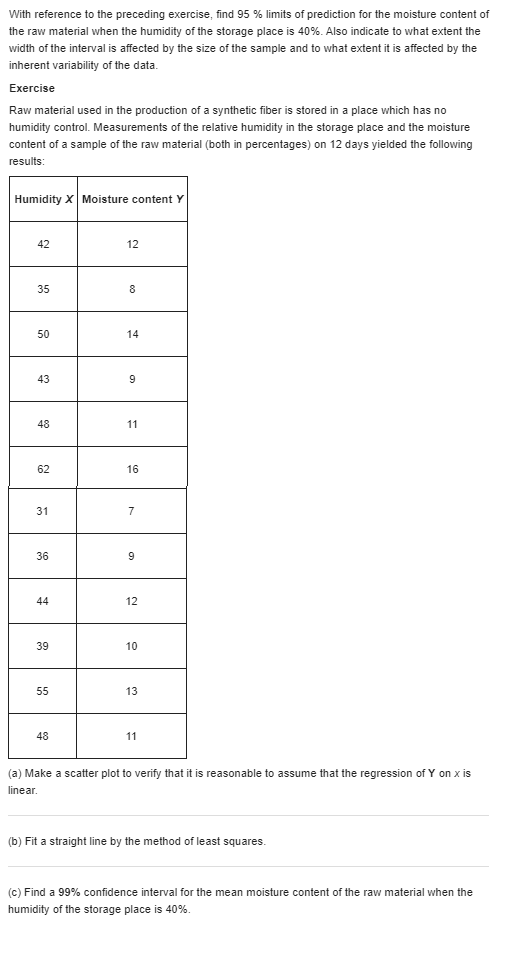
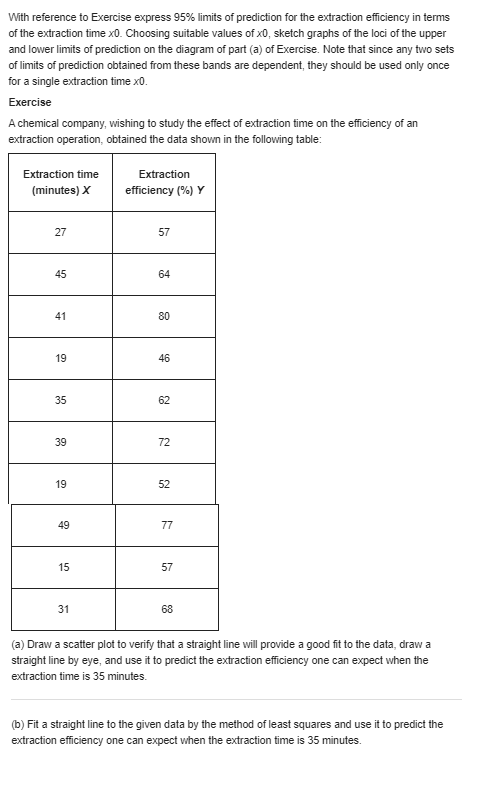
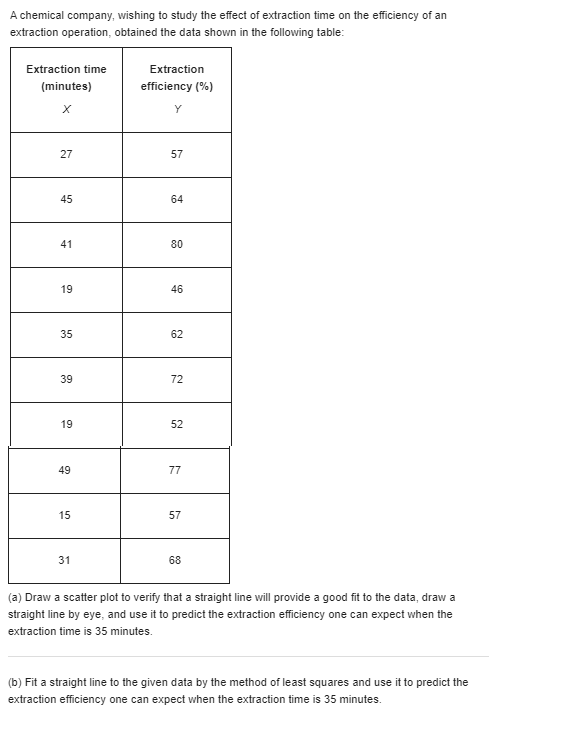
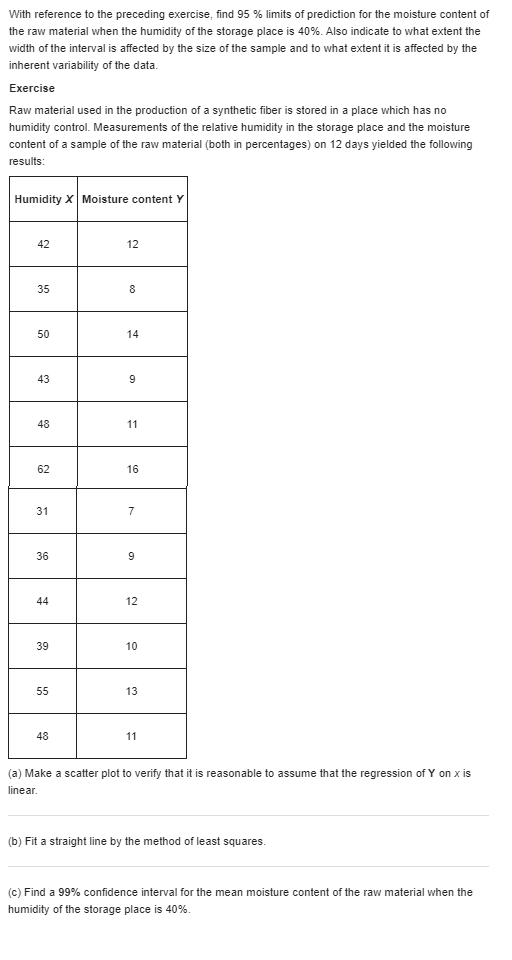
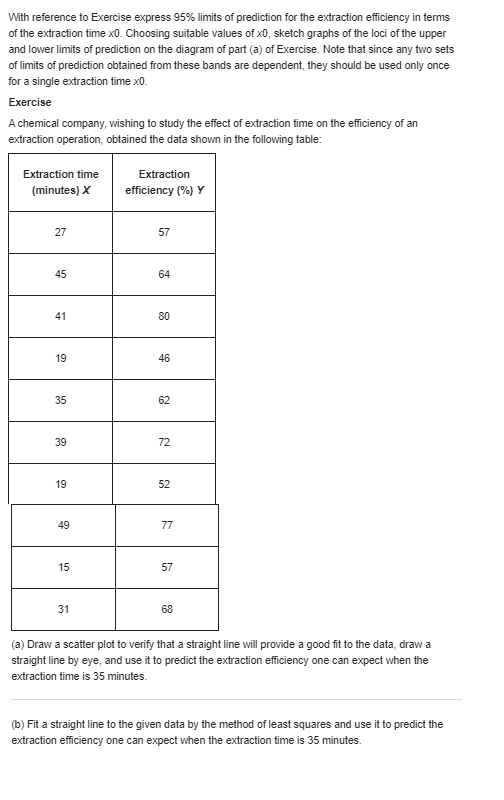
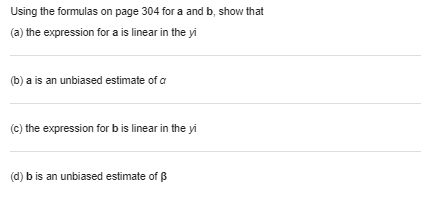
With reference to the preceding exercise, find 95 % limits of prediction for the moisture content of the raw material when the humidity of the storage place is 40%. Also indicate to what extent the width of the interval is affected by the size of the sample and to what extent it is affected by the inherent variability of the data. Exercise Raw material used in the production of a synthetic fiber is stored in a place which has no humidity control. Measurements of the relative humidity in the storage place and the moisture content of a sample of the raw material (both in percentages) on 12 days yielded the following results: Humidity X |Moisture content Y 42 12 35 8 50 14 43 9 48 11 62 16 31 7 36 9 44 12 39 10 55 13 48 11 (a) Make a scatter plot to verify that it is reasonable to assume that the regression of Y on x is linear. (b) Fit a straight line by the method of least squares. (c) Find a 99% confidence interval for the mean moisture content of the raw material when the humidity of the storage place is 40%.With reference to Exercise express 95% limits of prediction for the extraction efficiency in terms of the extraction time x0. Choosing suitable values of x0, sketch graphs of the loci of the upper and lower limits of prediction on the diagram of part (a) of Exercise. Note that since any two sets of limits of prediction obtained from these bands are dependent, they should be used only once for a single extraction time x0. Exercise A chemical company, wishing to study the effect of extraction time on the efficiency of an extraction operation, obtained the data shown in the following table: Extraction time Extraction (minutes) X efficiency (%) Y 27 57 45 64 41 80 19 46 35 62 39 72 19 52 49 77 15 57 31 68 (a) Draw a scatter plot to verify that a straight line will provide a good fit to the data, draw a straight line by eye, and use it to predict the extraction efficiency one can expect when the extraction time is 35 minutes. (b) Fit a straight line to the given data by the method of least squares and use it to predict the extraction efficiency one can expect when the extraction time is 35 minutes.When the sum of the x values is equal to zero, the calculation of the coefficients of the regression line of Y on x is greatly simplified; in fact, their estimates are given by and = Exy This simplification can also be attained when the values of x are equally spaced; that is, when they are in arithmetic progression. We then code the data by substituting for x the values . .., -2,-1, 0, 1, 2, . ... when n is odd, or the values . ..,-3,-1, 1, 3, ..., when n is even. The preceding formulas are then used in connection with the coded data. (a) Because of high lead residue, a faucet manufacturer cannot sell his product for home use unless each item is labeled as being hazardous to health. A consulting engineer suggests adding an acid bath at the end of the production line. An experiment is conducted with the bath having 0.2, 0.4, 0.6, 0.8, 1.0, 1.2 and 1.4 percent acid solutions. Suppose the corresponding values of lead residue are 4.6, 4.0, 3.3, 3.6, 3.0, 2.4, and 1.6 ppm. Fit a least squares line and give the point prediction of the lead residue when using a 1.3 percent solution. (b) Encouraged by the responses in Part (a), one further test was conducted with a 1.6 percent solution. Suppose the resulting lead residue is 1.1 ppm. Fit a least squares line using all eight runs. Again predict the lead residue for a 1.3 percent solutionA chemical company, wishing to study the effect of extraction time on the efficiency of an extraction operation, obtained the data shown in the following table: Extraction time Extraction (minutes) efficiency (%) X Y 27 57 45 64 41 80 19 46 35 62 39 72 19 52 49 77 15 57 31 68 (a) Draw a scatter plot to verify that a straight line will provide a good fit to the data, draw a straight line by eye, and use it to predict the extraction efficiency one can expect when the extraction time is 35 minutes. (b) Fit a straight line to the given data by the method of least squares and use it to predict the extraction efficiency one can expect when the extraction time is 35 minutes.\fWith reference to the preceding exercise, test the null hypothesis 8 = 1.2 against the alternative hypothesis 8