Help with R!!! Obviously you dont have to do it, I just want the codes and the explanations. Would greatly appreciate it.

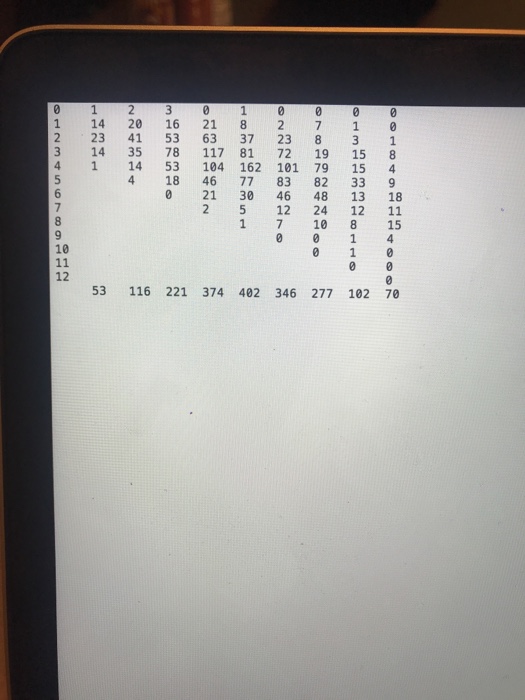
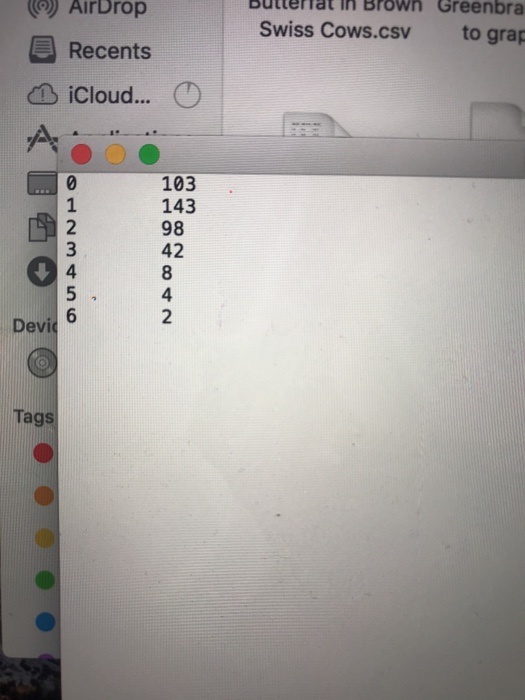
in order to Hint: See the on-line handout, Some Analysis of the Prussian Army "Death by Horsekick" Data. This will help with parts A and B. Here is what you need to do for this assignment. PART A: Binomial Distribution Questions, Some Using the Pig Litter Data Al. Obtain a barplot of the empirical (observed) frequencies for litters of size n 7 A2. Obtain a barplot of the expected frequencies if we use a binomial distribution with parameters n 7 and p 0.5, A3. Obtain a barplot of the expected frequencies if we use a binomial distribution with n 7 and p estimated from the data in litters of size 10 only. How do the three graphs in Al to A3 compare? Put the graphs on one page and hand this in; the command par (ntrow - c(3,1)) helps do this in A4. Calculate the (chi-square) goodness-of-fit values between (i) the observed frequencies and the expected frequencies in A2 and (ii) the observed frequencies and expected frequencies in A3. Note you will likely have to pool from both ends. How do the two values compare? A5. Use the dbinom) function to generate binomial probability distributions, all withn 20 but varying -0.05,0.10, 0.25, 0.75, 0.90, 0.95. Use barplos0 to graph each distribution. You do not need to the graphs in, but you are to describe two important pattens you should see as p changes. PART B: Poisson Distribution Questions, Some Using the Yeast Count Data BI. Use R to obtain a barplot of the empirical frequencies of the yeast count data. B2. Obtain the (sample) mean yeast cell count per sampling unit. Using the sample mean to estimate lambda, obtain the expected frequencies for a Poisson distribution. Make a frequencies. Based on the barplots, how closely do the observed and expected expected freot of the expestc ies match? B3. Calculate the value of the chi-square goodness-of-fit statistie between the observed and expected frequencies. Pool where necessary, use the threshold that all expected frequencies must be at least 3. (Hints on the pooling will be given in class.) B4. Generate a random sample of 10,000 observations from a Poisson - 1.7) distribution Obtain a frequency table with the table) command. Convert this to a relative fre frequencies are empirical probabilities, how do these compare with the theortical probabilities for x -0 to 9 and 10+? What are the values of the sample mean and sample yariance for the sample data you generated? How do these values compare to the population parameter values? cy table. Relative the dpois) function to generate probability distributions of Poisson random variables for 0.4, 1.2, 3.6.Use barplot0 to graph each distribution. You do not need to hand these tell us how the shape of the Poisson distribution changes here as increases graphs in, but do F7 Dll F8 F9 F10 F11 F12