Help with this question??? Thank You! (Please answer specifically, thank you!)

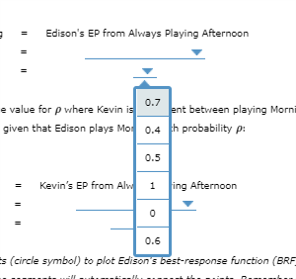
4. Computing mixed-strategies equilibria Just like any other undergraduate student, Edison knows the importance of arriving before his roommate when it comes to moving into his dorm room. However, he also recognizes the difficulty in moving at exactly the same time as his roommate; everyone is cramped in the stairways, hallways, and in the elevator, and there's a limit to the number of bodies that can fit in that small room at once to unpack. Since Edison is a first-year student, the university assigned Kevin to be his roommate. Assume that it is impossible for either roommate to get in touch with the other one prior to move-in day. So each roommate must decide simultaneously whether to arrive in the morning or afternoon. If they move in at the same time, each receives a payoff of O: if they move in at different times, each receives a positive payoff, but the person arriving in the morning is better off. The following payoff matrix represents the game they must play. Kevin Morning Afternoon Morning 0, 0 15, 10 Edison Afternoon 10. 15 A mixed-strategy equilibrium is one in which each player assigns a probability distribution over the possible pure strategies. In this particular game, this means that each person will play Morning with a certain probability and Afternoon with 1 minus that probability. To solve for the mixed- strategy equilibria, you must first determine each person's best response, given the strategy of the other player. Let A be the probability that Kevin plays Morning, and p be the probability that Edison plays Morning. Based on the payoff matrix, you know that each player's goal is to arrive on move-in day at different times. Use the following table to match Edison's best response when Kevin plays A = 1 and * = 0. A=1 A=0 p=0 O p=1 O O It turns out that for almost all values of A, Edison's best response is to play p = 0 or p= 1. However, there is a certain value of A that Kevin may play where Edison is actually indifferent between all possible mixed strategies that he could play (the proof of this is beyond the scope of this question). To determine this value for A, you can simply set the expected payoff (EP) for Edison when he plays Morning with 100%% probability (p = 1) equal to the expected payoff when he plays Afternoon with 100%% probability (p =0), given that Kevin plays Morning with probability A: Edison's EP from Always Playing Morning Edison's EP from Always Playing AfternoonOn the following graph, use the blue points (circle symbol) to plot Edison's best-response function (BRF), and use the purple points (diamond symbol) to plot Kevin's best-response function. Line segments will automatically connect the points. Remember to plot from left to right. Then, place black points (plus symbol) to indicate all mixed strategy Nash equilibria of this game. 1.0 O Edison's BRF Kevin's BRF 0.5 0.4 Nash Equilibria 0.3 0.1 02 03 0.4 05 0.6 0.7 0.8 0.9 1.0 AEdison's EP from Always Playing Morning A(10) + (1 - A)(O) Using the A(15) + (1 - A)(0) ists a unique va Afternoon sy () = 0), give MO) + (1 - A)(15)Edison's EP from Always Playing Afternoon A(10) + (1 - A)(0) for p whe A(15) + (1 - A)(0) between playing Morning w hat Edison robability p: A(0) + (1 - A) (15)Edison's EP from Always Playing Afternoon 0.7 e value for p where Kevin is ent between playing Morn given that Edison plays Mo 0.4 th probability p: 0.5 = Kevin's EP from Alw 1 ing Afternoon 0.6 s (circle symbol) to plot Edison's best-response function (BRFKevin's EP from Always Playing Morning p(15) + (1 - p)(0) On the f p(0) + (1 - p)(15) e blue points to plot K Function. Line points p(10) + (1 - p)(0) e all mixed stKevin's EP from Always Playing Afternoon p(10) + (1 - p)(0) (circle symbol p(15) + (1 - p)(0) response function (BRF), and segments will t the points. Remember to ple trategy Nash e p(0) + (1 - p)(15)Kevin's EP from Always Playing Afternoon (circle symbol) to ple 0.7 's best-response function (BRF), and segments will autom 0.4 connect the points. Remember to ple trategy Nash equilibria game. 0.6 0 0.5