Help with VPR problem, I have attached the problem formulation and the implementation which doesn't work.

I have made the following program from the given data, but it says that there are no feasible solution. Hope someone can help me solve the problem.

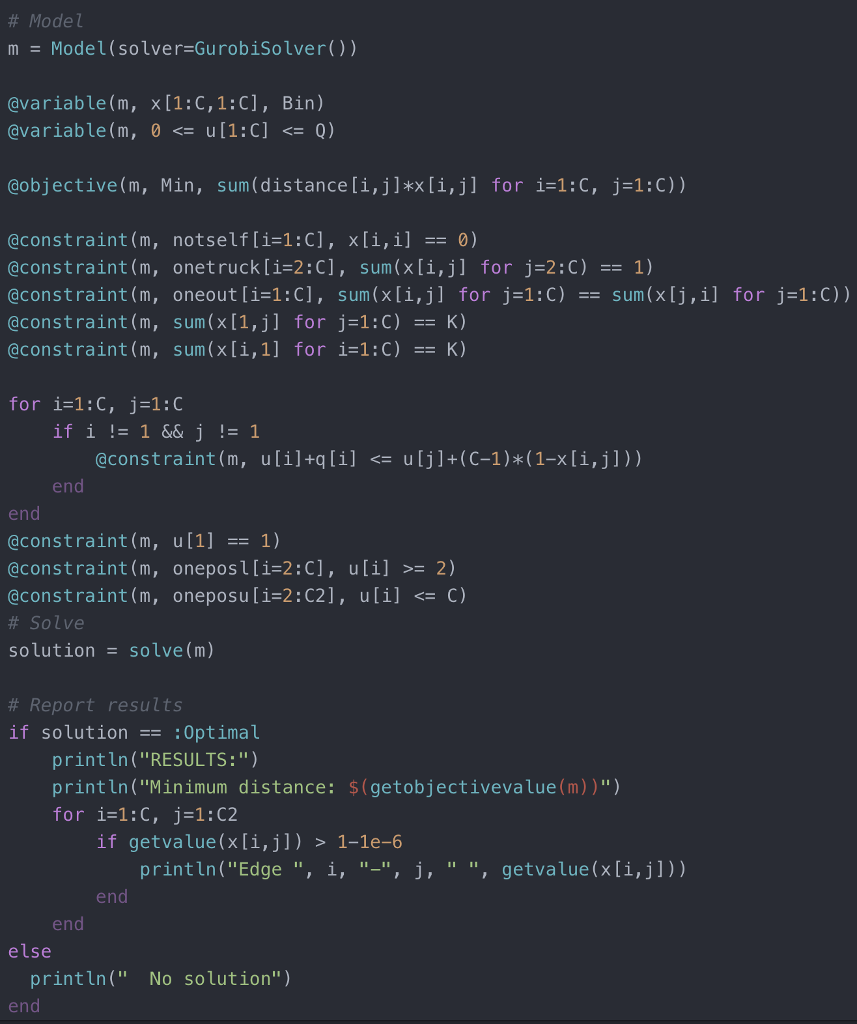
Data:

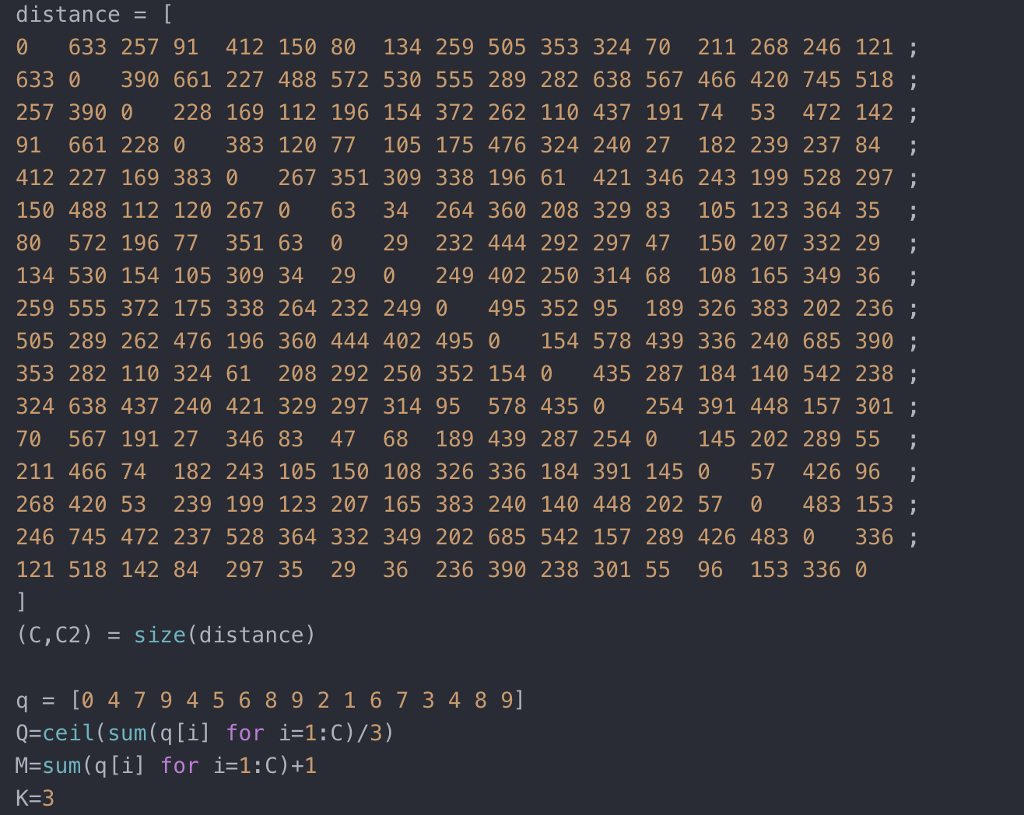
Minimize subject to . Dj d(i,j) . x(i j di A few comments on the constraints e There are i E I depot and customers, where the first (1) is the depot e The variables c(.j) are binary, and 1 if one truck drives from i to j . The trucks have identical capacity Q and each customer has requires qi goods . The wi variables are the counting variables, as in the TSP, but this time with an upper bound corresponding to the truck capacity . The first constraint ensures that at each customer (notice, not the depot) exactly one truck arrives . The seco nd constraint ensures that the truck which arrives to a customer from some other customer or depot also leaves the customer K truck-routes leaves the depot and arrives at the depot . The third and fourth constraint ensures that . Finally, the extended TSP counting constraint: If a variable au) 1 then w I then wi > wi + qi. Hence the counting variable both breakes closed tours and ensures that the truck tours do not exceed the capacity w of the trucks Q Impement the above model in Julia/JuMP. You can download an example with a depot and 16 customers example using 3 trucks, from campusnet "VRP_17_3.j1" Optimal solution for Vehicle Routing Problem: 2473 (Gurobi: 14 sec. GLPK: > 40 min.) # Model mModel(solver GurobiSolver()) @variable(m, x[1:C,1:C], Bin) @variable (m, 0 = 2) @constraint(m, oneposu[i-2:C2], uli] 1-1e-6 println("Edge ", i, "-", j, "", getvalue (x[i,j])) end end else println(" No solution") end distance[ 0 633 257 91 412 150 80 134 259 505 353 324 70 211 268 246 121; 633 0 390 661 227 488 572 530 555 289 282 638 567 466 420 745 518 257 3900 228 169 112 196 154 372 262 110 437 191 74 53 472 142 91 661 2280 383 120 77 105 175 476 324 240 27 182 239 237 84 412 227 169 383 0 267 351 309 338 196 61 421 346 243 199 528 297; 150 488 112 120 2670 63 34 264 360 208 329 83 105 123 364 35 80 572 196 77 351 63 029 232 444 292 297 47 150 207 332 29 134 530 154 105 309 34 29 0 249 402 250 314 68108 165 349 36 259 555 372 175 338 264 232 249 0 495 352 95 189 326 383 202 236 505 289 262 476 196 360 444 402 495 0 154 578 439 336 240 685 390 353 282 110 324 61 208 292 250 352 154 0 435 287 184 140 542 238 324 638 437 240 421 329 297 314 95 578 435 0 254 391 448 157 301; 70 567 191 27 346 83 4768 189 439 287 2540 145 202 289 55 ; 211 466 74 182 243 105 150 108 326 336 184 391 1450 57 426 96 268 420 53 239 199 123 207 165 383 240 140 448 202 57 0483 153; 46 745 472 237 528 364 332 349 202 685 542 157 289 426 483 0 336 121 518 142 84 297 35 29 36 236 390 238 301 55 96 153 3360 (C, C2) size(distance) q[0 479456892167 3489] Q-ceil(sum(qli] for i-1:C)/3) M-sum(q li] for i-1:C)+1 Minimize subject to . Dj d(i,j) . x(i j di A few comments on the constraints e There are i E I depot and customers, where the first (1) is the depot e The variables c(.j) are binary, and 1 if one truck drives from i to j . The trucks have identical capacity Q and each customer has requires qi goods . The wi variables are the counting variables, as in the TSP, but this time with an upper bound corresponding to the truck capacity . The first constraint ensures that at each customer (notice, not the depot) exactly one truck arrives . The seco nd constraint ensures that the truck which arrives to a customer from some other customer or depot also leaves the customer K truck-routes leaves the depot and arrives at the depot . The third and fourth constraint ensures that . Finally, the extended TSP counting constraint: If a variable au) 1 then w I then wi > wi + qi. Hence the counting variable both breakes closed tours and ensures that the truck tours do not exceed the capacity w of the trucks Q Impement the above model in Julia/JuMP. You can download an example with a depot and 16 customers example using 3 trucks, from campusnet "VRP_17_3.j1" Optimal solution for Vehicle Routing Problem: 2473 (Gurobi: 14 sec. GLPK: > 40 min.) # Model mModel(solver GurobiSolver()) @variable(m, x[1:C,1:C], Bin) @variable (m, 0 = 2) @constraint(m, oneposu[i-2:C2], uli] 1-1e-6 println("Edge ", i, "-", j, "", getvalue (x[i,j])) end end else println(" No solution") end distance[ 0 633 257 91 412 150 80 134 259 505 353 324 70 211 268 246 121; 633 0 390 661 227 488 572 530 555 289 282 638 567 466 420 745 518 257 3900 228 169 112 196 154 372 262 110 437 191 74 53 472 142 91 661 2280 383 120 77 105 175 476 324 240 27 182 239 237 84 412 227 169 383 0 267 351 309 338 196 61 421 346 243 199 528 297; 150 488 112 120 2670 63 34 264 360 208 329 83 105 123 364 35 80 572 196 77 351 63 029 232 444 292 297 47 150 207 332 29 134 530 154 105 309 34 29 0 249 402 250 314 68108 165 349 36 259 555 372 175 338 264 232 249 0 495 352 95 189 326 383 202 236 505 289 262 476 196 360 444 402 495 0 154 578 439 336 240 685 390 353 282 110 324 61 208 292 250 352 154 0 435 287 184 140 542 238 324 638 437 240 421 329 297 314 95 578 435 0 254 391 448 157 301; 70 567 191 27 346 83 4768 189 439 287 2540 145 202 289 55 ; 211 466 74 182 243 105 150 108 326 336 184 391 1450 57 426 96 268 420 53 239 199 123 207 165 383 240 140 448 202 57 0483 153; 46 745 472 237 528 364 332 349 202 685 542 157 289 426 483 0 336 121 518 142 84 297 35 29 36 236 390 238 301 55 96 153 3360 (C, C2) size(distance) q[0 479456892167 3489] Q-ceil(sum(qli] for i-1:C)/3) M-sum(q li] for i-1:C)+1