HERE ARE MY QUESTIONS

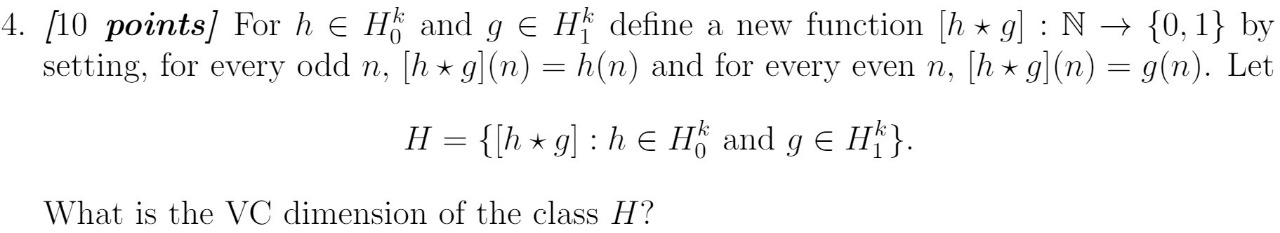
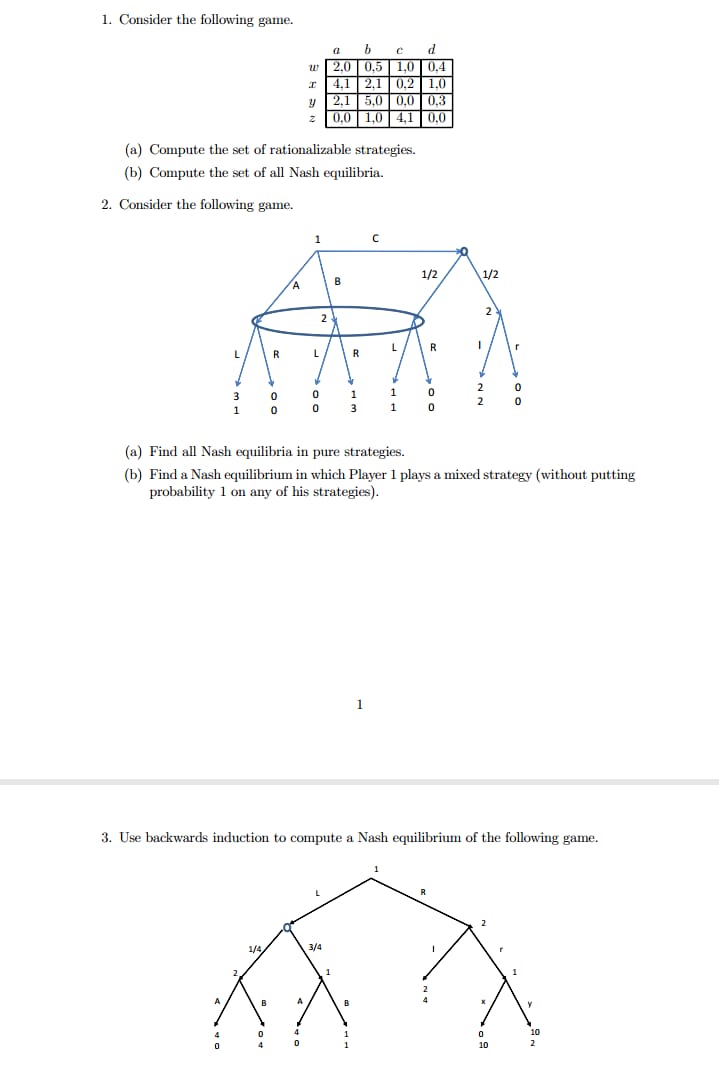
Question 4 A game G = (N. S, u) is said to be symmetric if S1 = $2 = ... = S,, and there is some function f : S, x S- - R such that f(s,, s_,) is symmetric with respect to the entries in s_i, and w; (s) = f (si, $_;) for every player i. (1) Consider a symmetric game G = (N. S, u) in which S, is a compact and convex subset of a Euclidean space and u, is continuous and quasiconcave in s;. Show that there exists a symmetric pure-strategy Nash equilibrium (i.e. a pure-strategy Nash equilibrium where every player uses the same strategy). (2) Suggest a definition for symmetric Bayesian games, G = (N. A. O, u, T, p), and find broad conditions on such a game G that ensure that G has a symmetric Bayesian Nash equilibrium. (3) Consider a Cournot oligopoly with inverse-demand function P and a cost function y that is common to all firms. Each firm's cost depends on its production level and its idiosyncratic cost parameter, which is drawn from a finite set C. Assume the vector of cost parameters (C1, . .., (,) is symmetrically distributed. Each firm i privately knows its own cost c, but not the others' costs, and independently chooses a quantity q; to produce. Find conditions on P and y that guarantee existence of a symmetric Bayesian Nash equilibrium in this game. (Note that the profit of each firm i is q;P (qi + . . - + qn) - 7 (qi, G).)4. [10 points] For h E H, and g E HE define a new function [h x g] : N - {0, 1} by setting, for every odd n, [h x g](n) = h(n) and for every even n, [h x g](n) = g(n). Let H = { [h x g] : he H; and g E H}}. What is the VC dimension of the class H?Question 1 Provide an example of a 2-player game with strategy set [0, co) for either player and payoffs continuous in the strategy profile, such that no strategy survives iterated deletion of strictly dominated strategies (S* = 0), but the set of strategies remaining at every stage is nonempty (S* * 0 for k = 1, 2, ...). Question 2 In the normal form game below player 1 chooses rows, player 2 chooses columns, and L R LR LR L R U 9 0 U 0 9 U 0 0 U 6 0 D 0 D 9 D D 0 6 A B D player 3 chooses matrices. We only indicate player 3's payoff. Show that action D is not a best response for player 3 to any independent belief about opponents' play (mixed strategy for players 1 and 2), but that D is not strictly dominated. Comment. Question 3 Each of two players i = 1, 2 receives a ticket with a number drawn from a finite set Oj. The number written on a player's ticket represents the size of a prize he may receive. The two prizes are drawn independently, with the value on i's ticket distributed according to F. Each player is asked simultaneously (and independently) whether he wants to exchange Date: February 17, 2016. 2 MIHAI MANEA his ticket for the other player's ticket. If both players agree then the prizes are exchanged; otherwise each player receives his own prize. Find all Bayesian Nash equilibria (in pure or mixed strategies).1. Consider the following game. b 2.0 0.5 1,0 0,4 4.1 2.1 0.2 NEH 2.1 5,0 0.0 0.3 0.0 1,0 4.1 0,0 (a) Compute the set of rationalizable strategies. (b) Compute the set of all Nash equilibria. 2. Consider the following game. 1 C 1/2 B 1/2 R (a) Find all Nash equilibria in pure strategies. (b) Find a Nash equilibrium in which Player 1 plays a mixed strategy ( without putting probability 1 on any of his strategies). 3. Use backwards induction to compute a Nash equilibrium of the following game. R 314 104. A unit mass of kids are uniformly located on a street, denoted by the [0, 1] interval. There are two ice cream parlors, one located in a and the other is located in 1 - r, where r 0. Given the prices p and q for the ice cream in stores located at r and 1 - r, respectively, each kid buys one unit of ice cream from the store with the lowest total cost, which is the sum of the price and the cost to go to the store. (If the total cost is the same, she flips a coin to choose the store to buy.) (a) Compute the revenue for each firm, as a function of price vector (p, q). The revenue is price times the total mass of the kids who buy from the given store. (b) Assume that each store set their own price simultaneously and try to maximize the expected value of its own revenue, as computed in part (a). Write this game in normal form. (c) Compute the set of Nash equilibria. (d) Compute the set of rationalizable strategies.Start with approximation x0 to the root of function f(x), the function evaluated at x0, and the derivative of the function evaluated at x0. Compute a better approximation the root using _ x) f'(x,--1) xi = xil Use a whi l e loop in the function, and return both the estimated root and the number of iterations used in the loop; e.g.: return r, n