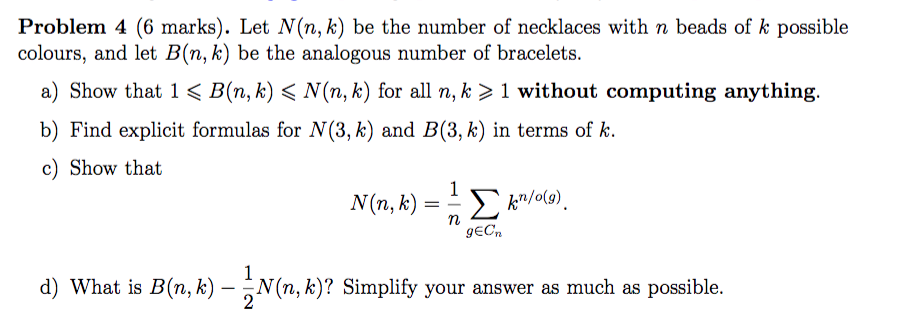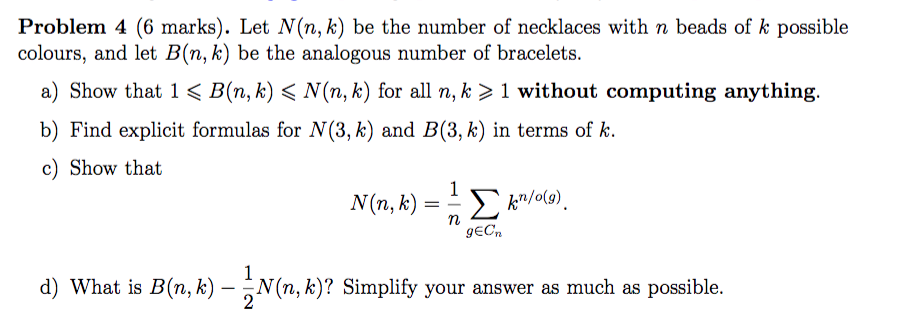
Here are some hints for part b,c,d

hint for part b) is showed below

Problem 4 (6 marks). Let N(n,k) be the number of necklaces with n beads of k possible colours, and let B(n,k) be the analogous number of bracelets. a) Show that 1 1 without computing anything. b) Find explicit formulas for N(3,k) and B(3,k) in terms of k. c) Show that 1 N(a, k) kn/o(9) geCa n 1 d) What is B(n, k) N(n, k)? Simplify your answer as much as possible. b) Lecture 18, Slide 39f. c) The (g)-orbit of any bead in a necklace fixed by g is monochromatic. d) The answer depends on the parity of n. Example (Mathematical jewellery) We can use Burnside's lemma to count the distinct colourings of necklaces and bracelets. Let X be the set of all 33 = 27 different ways of making jewellery with 3 beads and 3 colours. The groups that act on X are D3 = (r, f) (for bracelets) and its subgroup C3 = (r) (for necklaces). To count the number of orbits, we'll take the average of |XS| over all g in G. is Example (continued...) 1. [Xe] = 27 i.e. the identity element fixes all 27 arrangements. 2. IX'] = [Xr21 = 3 because both nontrivial rotations (by 120 or 240) fix just the 3 monochromatic necklaces. At this point, we immediately deduce that the number of necklaces 33 5127 (27 +3+3) = = 11. 3 3. |xf= |xfr| = xfr21 = 32 = 9 because a piece of jewellery is fixed by a reflection iff the two beads on either side of the axis have the same colour. Therefore, the number of bracelets is 60 27 (27 +3+3+9+9+9) = = 10. 6 6 Problem 4 (6 marks). Let N(n,k) be the number of necklaces with n beads of k possible colours, and let B(n,k) be the analogous number of bracelets. a) Show that 1 1 without computing anything. b) Find explicit formulas for N(3,k) and B(3,k) in terms of k. c) Show that 1 N(a, k) kn/o(9) geCa n 1 d) What is B(n, k) N(n, k)? Simplify your answer as much as possible. b) Lecture 18, Slide 39f. c) The (g)-orbit of any bead in a necklace fixed by g is monochromatic. d) The answer depends on the parity of n. Example (Mathematical jewellery) We can use Burnside's lemma to count the distinct colourings of necklaces and bracelets. Let X be the set of all 33 = 27 different ways of making jewellery with 3 beads and 3 colours. The groups that act on X are D3 = (r, f) (for bracelets) and its subgroup C3 = (r) (for necklaces). To count the number of orbits, we'll take the average of |XS| over all g in G. is Example (continued...) 1. [Xe] = 27 i.e. the identity element fixes all 27 arrangements. 2. IX'] = [Xr21 = 3 because both nontrivial rotations (by 120 or 240) fix just the 3 monochromatic necklaces. At this point, we immediately deduce that the number of necklaces 33 5127 (27 +3+3) = = 11. 3 3. |xf= |xfr| = xfr21 = 32 = 9 because a piece of jewellery is fixed by a reflection iff the two beads on either side of the axis have the same colour. Therefore, the number of bracelets is 60 27 (27 +3+3+9+9+9) = = 10. 6 6