Here is the code of binary search tree:

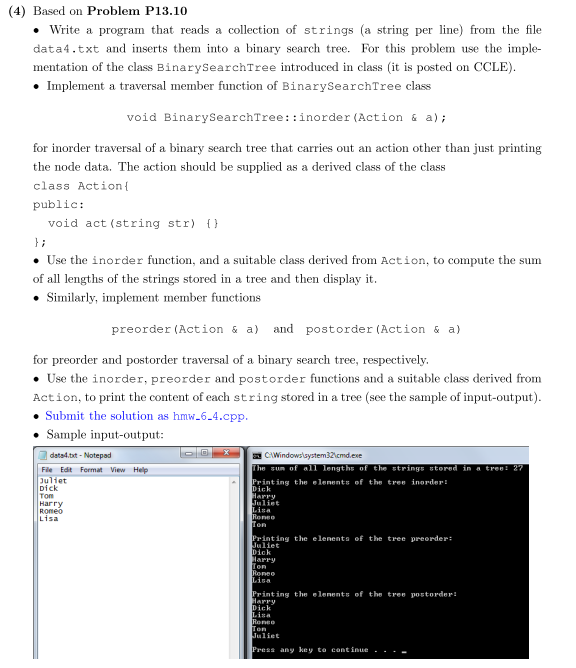
class TreeNode { public: void insert_node(TreeNode* new_node); void print_nodes() const; bool find(string value) const; private: string data; TreeNode* left; TreeNode* right; friend class BinarySearchTree; }; class BinarySearchTree { public: BinarySearchTree(); void insert(string data); void erase(string data); int count(string data) const; void print() const; private: TreeNode* root; }; BinarySearchTree::BinarySearchTree() { root = NULL; } void BinarySearchTree::print() const { if (root != NULL) root->print_nodes(); } void BinarySearchTree::insert(string data) { TreeNode* new_node = new TreeNode; new_node->data = data; new_node->left = NULL; new_node->right = NULL; if (root == NULL) root = new_node; else root->insert_node(new_node); } void TreeNode::insert_node(TreeNode* new_node) { if (new_node->data insert_node(new_node); } else if (data data) { if (right == NULL) right = new_node; else right->insert_node(new_node); } } int BinarySearchTree::count(string data) const { if (root == NULL) return 0; else if (root->find(data)) return 1; else return 0; } void BinarySearchTree::erase(string data) { // Find node to be removed and its parent TreeNode* to_be_removed = root; TreeNode* parent = NULL; bool found = false; while (!found && to_be_removed != NULL) { if (to_be_removed->data right; } else if (data data) { parent = to_be_removed; to_be_removed = to_be_removed->left; } else found = true; } if (!found) return; // to_be_removed contains data (and hence is not NULL) // If one of the children is empty, use the other if (to_be_removed->left == NULL || to_be_removed->right == NULL) { TreeNode* new_child; if (to_be_removed->left == NULL) new_child = to_be_removed->right; else new_child = to_be_removed->left; if (parent == NULL) // Found in root { delete to_be_removed; root = new_child; } else if (parent->left == to_be_removed) { delete to_be_removed; parent->left = new_child; } else { delete to_be_removed; parent->right = new_child; } return; } // Neither subtree is empty // Find smallest element of the right subtree TreeNode* smallest_parent = to_be_removed; TreeNode* smallest = to_be_removed->right; while (smallest->left != NULL) { smallest_parent = smallest; smallest = smallest->left; } // smallest contains smallest child in right subtree // Move contents, unlink child to_be_removed->data = smallest->data; if (smallest_parent == to_be_removed) { smallest_parent->right = smallest->right; delete smallest; } else { smallest_parent->left = smallest->right; delete smallest; } } bool TreeNode::find(string value) const { if (value find(value); } else if (data find(value); } else { return true; } } void TreeNode::print_nodes() const { if (left != NULL) left->print_nodes(); cout print_nodes(); }

Exercise P13.10. Use the inorder function of Exercise P13.9, and a suitable class derived from Action, to compute the sum of all lengths of the strings stored in a tree. (4) Based on Problem P13.10 Write a program that reads a collection of strings (a string per line) from the file data4.txt and inserts them into a binary search tree. For this problem use the imple- mentation of the class BinarySearchTree introduced in class (it is posted on CCLE) Implement a traversal member function of BinarySearchTree class void BinarySearchTree: :inorder (Action & a); for inorder traversal of a binary search tree that carries out an action other than just printing the node data. The action should be supplied as a derived class of the class class Action public: void act (string str) . Use the inorder function, and a suitable class derived from Action, to compute the sum of all lengths of the strings stored in a tree and then display it . Similarly, implement member functions preorder (Action &a) and postorder (Action&a) for preorder and postorder traversal of a binary search tree, respectively . Use the inorder, preorder and postorder functions and a suitable class derived from Action, to print the content of each string stored in a tree (see the sample of input-output) . Submit the solution as hmw-6-4.cpp . Sample input-output deta4.tot-Notepad Printing the elenents of the tree inorder Dick ick Harry uliet Printing the elenents of the tree preorder: ok Printing the lenents of the tree postorderl ick uliet Press any key to continue