Hey can you help me with this?

Everything is added with all the tables and definitions needed

Thank you.

The charts are to be answered and the questions below

thank you so much for your help

?Using the Dietary Reference Intakes to Assess Nutrient Intakes

Background Information

Specific nutrient requirements for any one person can only be determined by extensive metabolic testing for each and every nutrient. Instead of doing invasive and unpleasant human experimentation on each person, we can calculate estimates of your needs based on the DRI values that were extrapolated from data derived from an extensive collection of human scientific studies. The data can be used effectively for establishing population nutrient needs when the true individual nutrient requirements are normally distributed. This means that true human nutrient requirements would be distributed in a pattern that resembles the bell curve with a few people requiring nutrients on the low end or high end of the distribution and the majority falling within 1 standard deviation on either side of the mean (see explanation with diagrams in posted lecture). To assess the extent to which your dietary intake is likely to meet your own needs, specific nutrients from food intake data can be compared to the DRI values. Estimates for individuals are most reliable when complete records are collected for several days to reduce intra-individual variability. For us to assess a population for adequate nutrient intake, a large sample size is also important to reduce inter-individual variation.

Inter-individual variability (between subjects) refers to the variability of the nutrient requirement among a population of the same age and sex category based on the data from population studies. To estimate this value, we use a coefficient of variability (CV) that is specific for each nutrient. These values are established from a sufficient number of human studies for each nutrient and all available results are included in the DRI Book.

Intra-individual intake variability (within subjects) refers to the variability of nutrient intake from day to day for any one person. This is called the Within Subject Standard Deviation (WSSD) and these values are also included in the DRI book for each nutrient if they have been created.

Both values are essential for applying the formulas that are used to calculate dietary adequacy. All required values are provided for you within each exercise to help you answer each of the questions.

Definitions used for DRI values are provided below and also explained in your text.

Estimated Average Requirement (EAR):

The EAR is a nutrient intake value that is estimated to mean the nutrient intake needs for 50% of a specific age/sex group in the population. It is based on the accumulated evidence from biological assessments of many individual nutrient requirements. These are distributed in a statistically normal pattern (see bell curve below). The EAR can be used to assess the adequacy of intakes for an individual or a population. To use the EAR, you must calculate the probability of adequate intake using a formula that can account for dietary intake distributions for day-to-day variability (within subject standard deviations) and the variability of requirements (CV).

The requirements must be normally distributed; because iron requirements are not normally distributed for adult women, the probability approach cannot be used.

For an individual, a nutrient intake equal to the EAR has 50% probability of inadequacy; it also has a 50% probability of adequacy.For a precise estimate of probability of inadequate intake, we use the probability approach with the formula provided in class lecture.

Two options for assessing group intakes

1. The EAR "cut point" method

We can use the EAR to assess the adequacy of intake for a group; this is the technique used to assess the intake of Canadians from the CCHS national survey. The "cut point method is the proportion of the population with usual intakes below the EAR and it is the predicted prevalence of inadequate intakes if all assumptions are met.

1. The probability estimate based on population intake distributions

A more precise assessment is to estimate the predicted prevalence of inadequate intake using the probability approach as assigned in Question 3. You will compare the 2 methods in this question.

Recommended Dietary Allowance (RDA):

RDA values are calculated as 2 Standard Deviations above the EAR values to account for the needs of 97.5% of each age/sex group in the population. For an individual with a usual intake > RDA there is a low probability (2.5%) of inadequacy

Adequate Intake (AI):

Adequate intakes are determined for those nutrients that do not have EAR or RDA values. This is because there is insufficient data to create RDA values (e.g. Vitamin D and Vitamin K). For an individual, a usual dietary intake for a specific nutrient that exceeds the AI has low probability of inadequacy. For a group, a mean usual intake that exceeds the AI has low probability of inadequacy. No conclusions can be drawn if the usual intake is lower than AI

Tolerable Upper Level (UL):

The UL is the lowest intake level for which there has been an adverse outcome. These rarely occur with food intake and are primarily limited to cases of intakes from supplements or fortified products. For any individual with an intake above the UL there is a potential risk of adverse effects; you can estimate the probability of adverse effects with the formula in the DRI text on page 31. To do this you must document the sources of nutrients (food, fortification, pharmacological agents)

For a group, we can estimate the proportion of a population with usual intakes > UL to estimate those at risk of adverse effects

CDRR(Chronic Disease Risk Reduction)

A new category has been added to the DRI values to assess the impact of nutrients such as Sodium and Potassium intakes on the development or prevention of chronic disease.

For your assignment, apply each of the following exercises to the Cases

(Case #1 and 2)

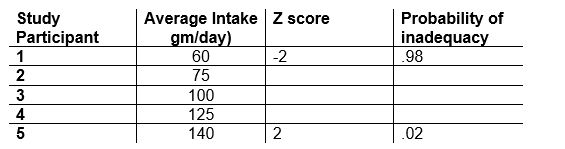
Probability approach using the EAR:

If you know the average nutrient intake of an individual, you can assess their probability of inadequate intake by:

1. obtaining an average nutrient intake for a known number of days
2. determining their Estimated Average Requirement (EAR) based on their age and sex (for the specific nutrient)
3. determining the Standard Deviation (SD) of the requirement (see Appendix H of the DRI book provided with class lecture notes); if the SD or coefficient of variation is 10%, the SD would be calculated by multiplying the EAR by 0.10)
4. determining the within person SD; see Appendix I of the DRI book provided with lecture notes
5. calculating their z score; see formula provided in class lecture
6. determining the probability (at 0.01) associated with the z score using the Table provided.(if the z score is a negative number, it is the probability of inadequate intake; if it is a positive number, it is the probability of adequate intake) the probability of inadequate intake = 1 - probability of adequate intake.

The value can be used to estimate the probability of inadequate intake of the individual.

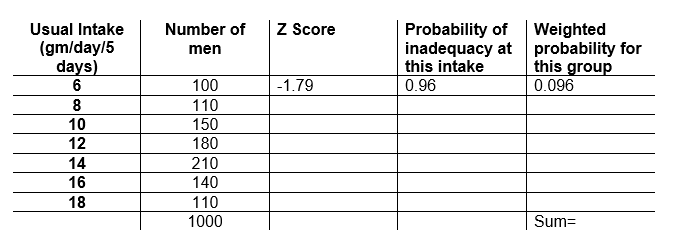
(Case #3)

To estimate the predicted prevalence of inadequate intake for the group, calculate the weighted average of all of the individual probabilities of inadequate intake. Directions are provided in the assignment. Read them carefully.

Using the Z table

Calculate the Z value from the formula (class lecture) and values provided in the assignment. Round off your score to 2 places beyond the decimal (e.g 1.6895 becomes 1.69) Look down the column (highlighted in yellow) under the Z to find the first 2 digits of your score(1.6). Look along that row and under the .09 to find the square in the Table that will tell you the P value (area under the curve). This is your estimated probability (0.9545); probability values always fall between -1 and 1. If the Z value is negative, it is the probability of inadequacy; if Z is positive, it is the probability of adequacy or you can deduct from 1.0 to find the probability of inadequacy (see examples on the assignment). We normally round off the values and express them at a %; this one would be 95%.

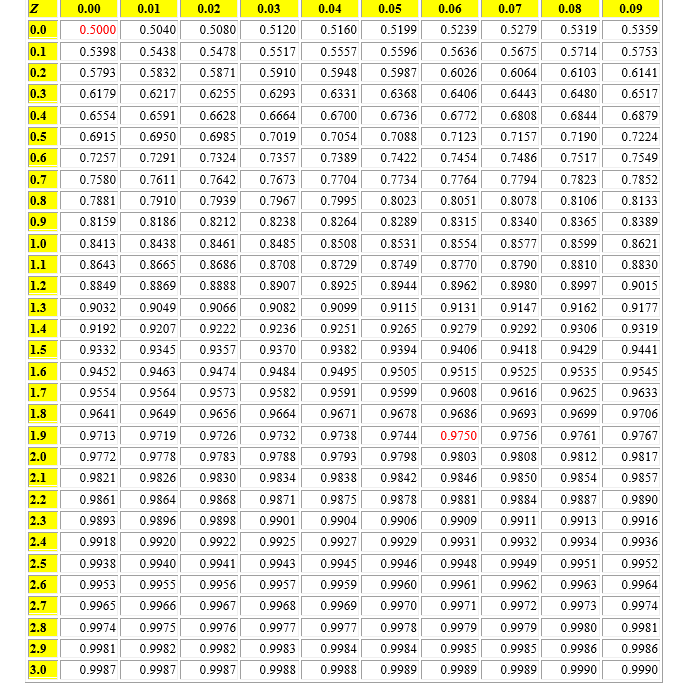
Standard Normal (Z) Table

Values in the table represent areas under the curve to the left of Z quantiles along the margins.

Usual Intake Number of Z Score Probability of Weighted (gm/day/5 men inadequacy at probability for days) this intake this group 6 100 -1.79 0.96 0.096 8 110 10 150 12 180 14 210 16 140 18 110 1000 Sum=