Hi all,

I have created the below circuit in logisim.

Now I just need to find a way to conect p and q to the divider to take the remainder as mod M and conected with my circuit so I will obtain the result base on formula ak=a^2k-1 mod M , please see attaches ! Any advice?

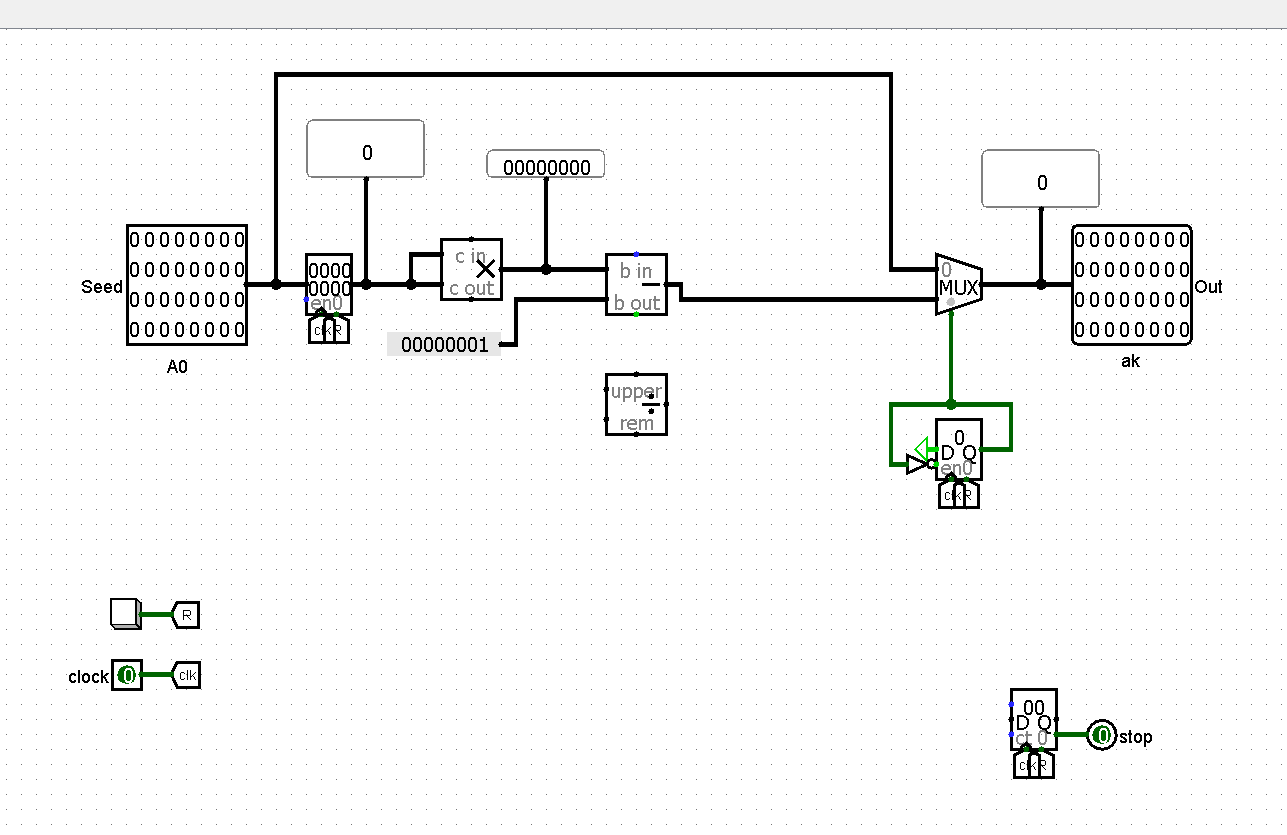
A 32-bit Blum-Blum-Shub pseudorandom number generator This is an interesting technique which is used in practice in the area of data security. For the purposes of encryption it is important to be able to generate a series of numbers that look and behave as if they were a digitally sampled random noise. More information can be found in Wikipedia, but this design exercise does not depend on your understanding of the intricacies of number theory. Here is what you need to do. The BBS sequence starts from an arbitrary number called "seed", which we will denote as a0. The generator is clocked, and it produces a 32-bit output ak every clock cycle k according to the following formula: ak=ak12modM Here pmodq is the remainder of the divison of p by q, for example, 10mod3=1,8mod4=0, etc. The choice of M is very important for the security and other properties of the generator. Again, we are only interested in the design aspect, so we will use a reasonably good number 5299956299=2983790701. It fits in 32 bits and ensures a long unpredictable (if the adversary does not know that M is a product of those particular prime numbers) sequence. Design particulars Use one 32-bit register for the current value of a and include in your circuit the multiplier and divider of the Arithmetic library. Note that the multiplier has the ability to multiply two 32-bit numbers to produce a 64-bit result in two separate 32-bit portions. Similarly, the divider divides a 64 -bit dividend by a 32-bit divisor producing a 32-bit quotient and a 32-bit remainder. Your circuit must input the seed in clock cycle 0 and produce 15 more results in subsequent clock cycles, raising the signal stop at the end of the 15 th cycle