Question: Hi everyone I need help with python and an intro to crypto class, I wish I never took this class because its so hard and
Hi everyone I need help with python and an intro to crypto class, I wish I never took this class because its so hard and I am not even a computer science major. Anything will be greatly appreciated .
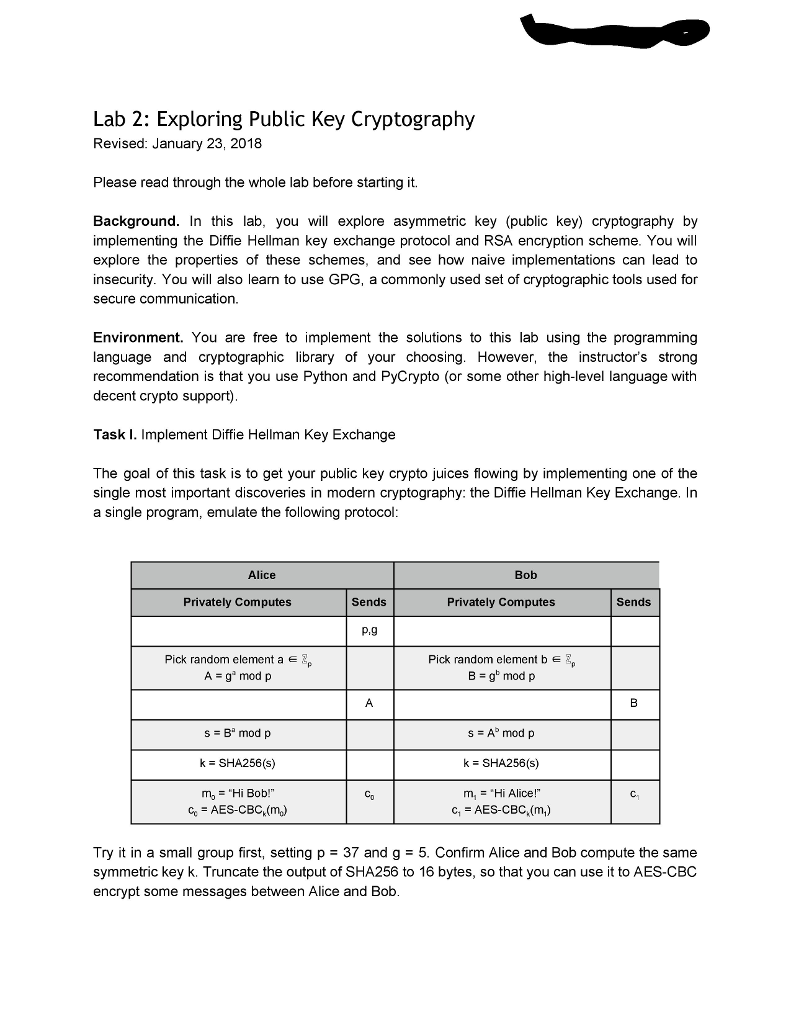

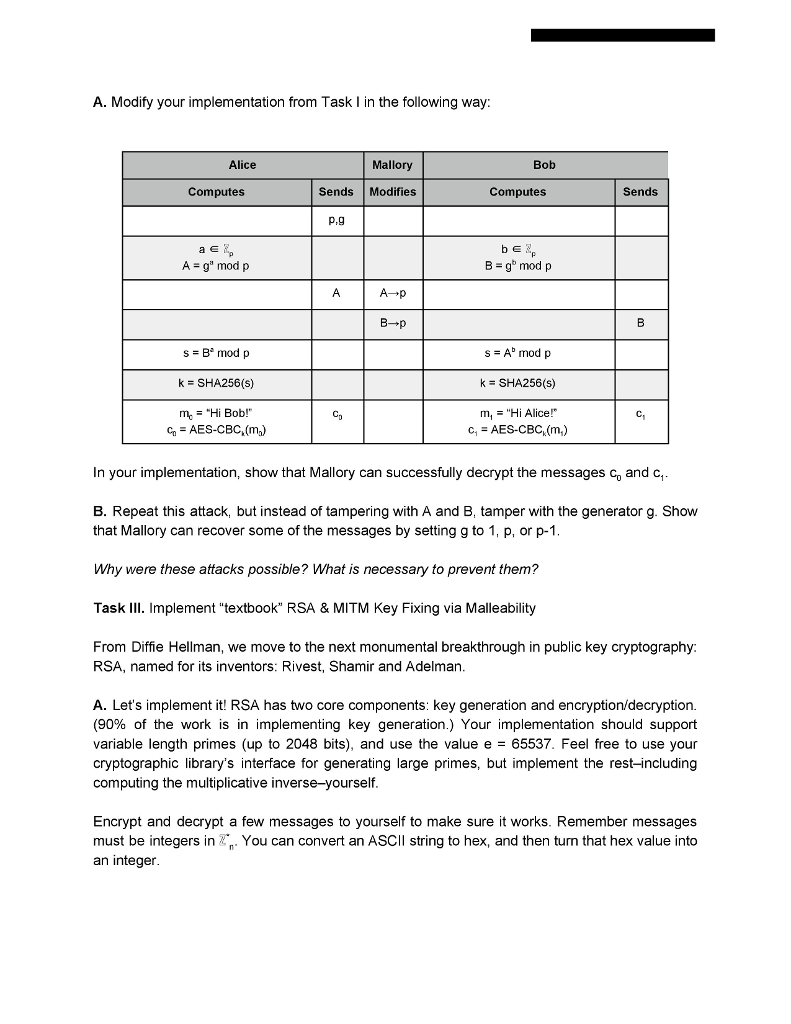
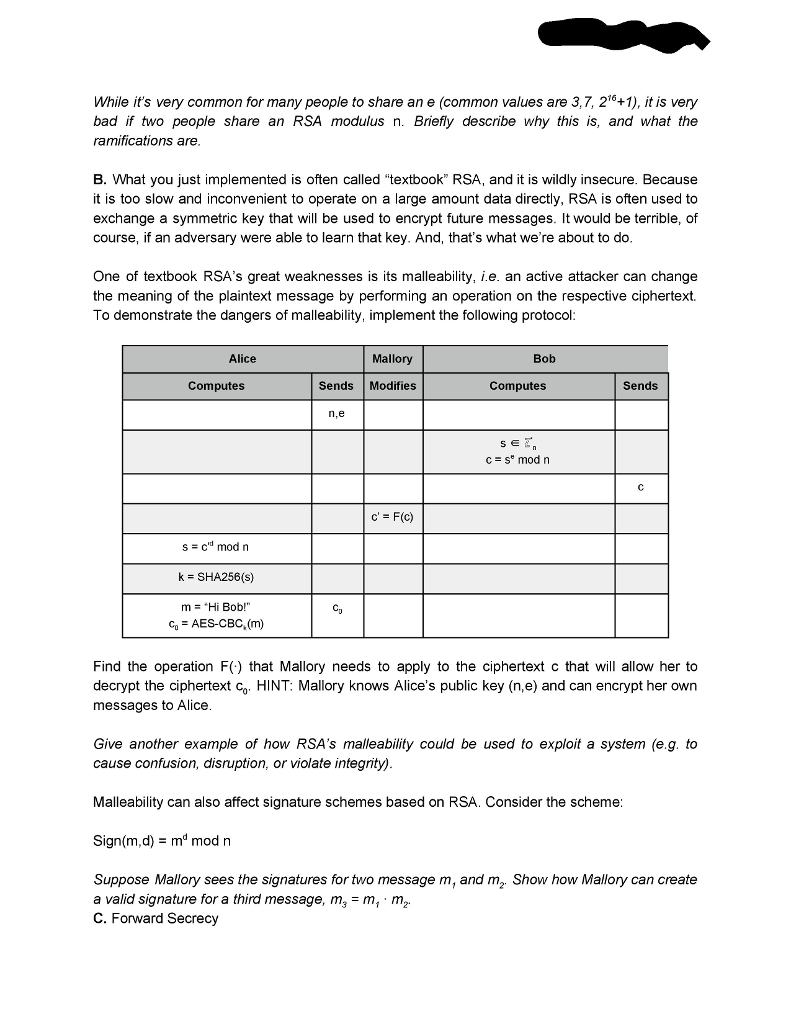
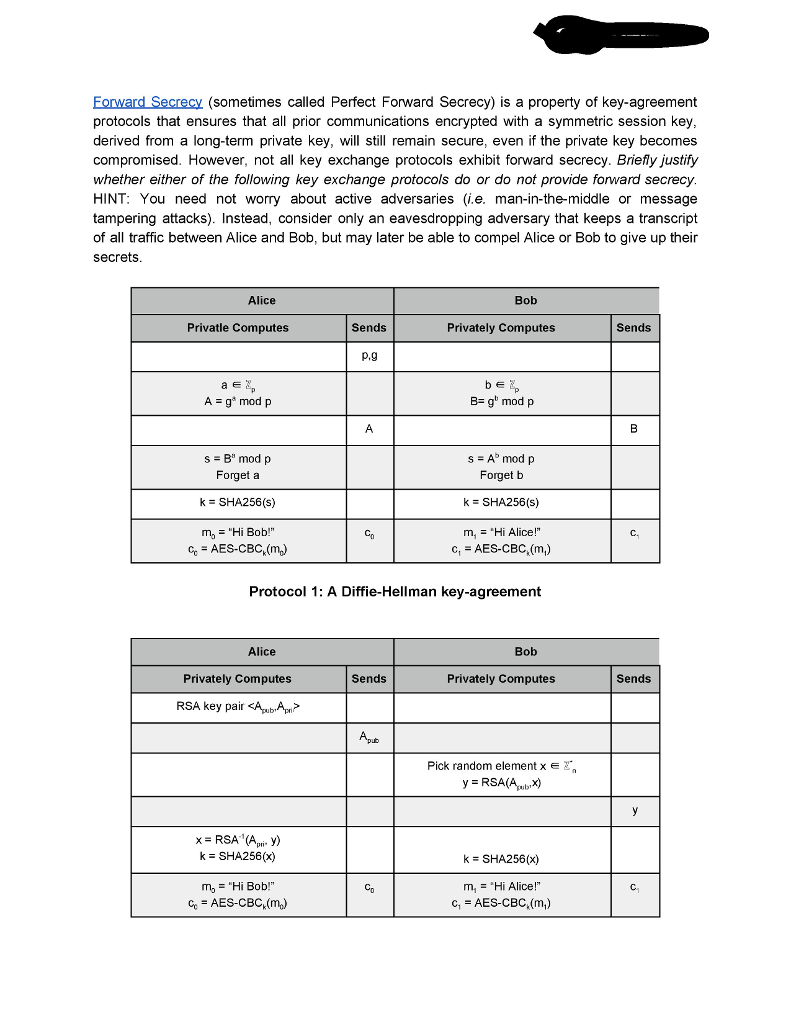

Lab 2: Exploring Public Key Cryptography Revised: January 23, 2018 Please read through the whole lab before starting it. Background. In this lab, you will explore asymmetric key (public key) cryptography by implementing the Diffie Hellman key exchange protocol and RSA encryption scheme. You will explore the properties of these schemes, and see how naive implementations can lead to insecurity. You will also learn to use GPG, a commonly used set of cryptographic tools used for secure communication. Environment. You are free to implement the solutions to this lab using the programming language and cryptographic library of your choosing. However, the instructor's strong recommendation is that you use Python and PyCrypto (or some other high-level language with decent crypto support) Task I. Implement Diffie Hellman Key Exchange The goal of this task is to get your public key crypto juices flowing by implementing one of the single most important discoveries in modern cryptography: the Diffie Hellman Key Exchange. In a single program, emulate the followin g protocol Alice Bob Privately Computes Sends Privately Computes Sends P.g Pick random element a e Pick random element b S A-g mod p B g mod p sA mod p k SHA256(s) m, "Hi Alice! k SHA256(s) m"Hi Bob!" CAES-CBC,(mo) C1-AES-CBC.(m.) Try it in a small group first, setting p- 37 and g 5. Confirm Alice and Bob compute the same symmetric key k. Truncate the output of SHA256 to 16 bytes, so that you can use it to AES-CBC encrypt some messages between Alice and Bob A. Modify your implementation from Task I in the following way: Alice Mallory Bob Computes Sends Modifies Computes Sends P,g A- g mod p B g mod p s Ab mod p k SHA256(s) m, "Hi Alice!" k SHA256(s) mo"Hi Bob!" CD Ci C,AES-CBC (m,) In your implementation, show that Mallory can successfully decrypt the messages c and c, B. Repeat this attack, but instead of tampering with A and B, tamper with the generator g. Show that Mallory can recover some of the messages by setting g to 1, p, or p-1 Why were these attacks possible? What is necessary to prevent them? Task IlI. Implement "textbook" RSA & MITM Key Fixing via Malleability From Diffie Hellman, we move to the next monumental breakthrough in public key cryptography RSA, named for its inventors: Rivest, Shamir and Adelman A. Let's implement it! RSA has two core components: key generation and encryption/decryption. (90% of the work is in implementing key generation.) Your implementation should support variable length primes (up to 2048 bits), and use the value e 65537. Feel free to use your cryptographic library's interface for generating large primes, but implement the rest-including computing the multiplicative inverse-yourself Encrypt and decrypt a few messages to yourself to make sure it works. Remember messages must be integers in You can convert an ASCIl string to hex, and then turn that hex value into an integer While it's very common for many people to share an e (common values are 3,7, 216+1), it is very bad if two people share an RSA modulus n. Briefly describe why this is, and what the ramifications are B. What you just implemented is often called "textbook" RSA, and it is wildly insecure. Because it is too slow and inconvenient to operate on a large amount data directly, RSA is often used to exchange a symmetric key that will be used to encrypt future messages. It would be terrible, of course, if an adversary were able to learn that key. And, that's what we're about to do One of textbook RSA's great weaknesses is its malleability, i.e. an active attacker can change the meaning of the plaintext message by performing an operation on the respective ciphertext. To demonstrate the dangers of malleability, implement the following protocol Alice Mallory Bob Computes SendsModifies Computes Sends n,e S E k SHA256(s) m "Hi Bob!" co AES-CBC.(m) C3 Find the operation F) that Mallory needs to apply to the ciphertext c that will allow her to decrypt the ciphertext c HINT: Mallory knows Alice's public key (n,e) and can encrypt her own messages to Alice Give another example of how RSA's malleability could be used to exploit a system (e.g. to cause confusion, disruption, or violate integrity Malleability can also affect signature schemes based on RSA. Consider the scheme Sign(m,d) m mod n Suppose Mallory sees the signatures for two message m, and m2 Show how Mallory can create a valid signature for a third message, m-m, m,2. C. Forward Secrecy (sometimes called Perfect Forward Secrecy) is a property of key-agreement protocols that ensures that all prior communications encrypted with a symmetric session key derived from a long-term private key, will still remain secure, even if the private key becomes compromised. However, not all key exchange protocols exhibit forward secrecy. Briefly justify whether either of the following key exchange protocols do or do not provide forward secrecy HINT: You need not worry about active adversaries (i.e. man-in-the-middle or message tampering attacks). Instead, consider only an eavesdropping adversary that keeps a transcript of all traffic between Alice and Bob, but may later be able to compel Alice or Bob to give up their secrets Alice Bob Privatle Computes Sends Privately Computes Sends p.g A g mod p B-g modp s B mod p Forget a k SHA256(s) m,-"Hi Bob!" s=A"mod p Forget b k = SHA256(s) m,"Hi Alice!" c, AES-CBC.(m) Co C1 e AES-CBC (m) Protocol 1: A Diffie-Hellman key-agreement Alice Bob Privately Computes Sends Privately Computes Sends RSA key pair Agub.pn? Pick random element x , x- RSA (Api. y) k SHA256x) k SHA256(x) Mg-"Hi Bob!" cAES-CBC,(m) m, "Hi Alice!" c, AES-CBC (m,) Protocol 2: An RSA key exchange Task IV. GPG: A Real Life Public Key Crypto Tool For this task, you will generate your own GNU Privacy Guard (GPG) public key pair using Keybase. Before Keybase came along, most users used the command line interface to GPG This web tutorial along with GPG's MiniHOWTO might show you how bad that actually is A. If you don't already have a public key, visit https://keybase.io, create an account, and generate a public key pair for yourself. Feel free to use the default parameters, or play with them as you see fit. If possible, verify yourself using a few methods. The idea being: the more methods authenticated methods you use, the more trust you build in the authenticity of your key B. Now, join the web of trust by "following" some of your friends, classmates, or me. Optionally you can use an HKP server, such as keys.gnupg.net, to publish and exchange keys. Be sure to verify the identity of the owner and key before signing it. Verifying the key's fingerprint with the owner over a "secure" or out-of-band channel (e.g. face-to-face, over the phone, or by trusting keybase's authentication techniques) is an easy way to do this C. Finally, encrypt and sign a message to Prof. Peterson and publish it as a plaintext attachment to the Secret Message discussion topic within the CPE321 Student Forum on PolyLearn. Feel free to use keybase's web or command-line interface to do this. For verification here is his key fingerprint: BC57A618547771A977BFBD14F94EFBEODSE6E6CB D. (Optional) If you don't want to use your key anymore you can destroy your keybase account. Task V. While the features provided by public key cryptography are attractive, they come at the cost of performance. In this task, you will quantify the performance differences between public and symmetric key algorithms. Fortunately, OpenSSL provides a simple interface for doing so openssl speed rsa and openssl speed aes will perform and measure their respective public and symmetric key operations using different parameters. One of the returned results for both operations is a measure of throughput operations per time (e.g. signatures per second). Run these operations and report your findings. Include two graphs: one that plots the block size vs. throughput for the various AES Lab 2: Exploring Public Key Cryptography Revised: January 23, 2018 Please read through the whole lab before starting it. Background. In this lab, you will explore asymmetric key (public key) cryptography by implementing the Diffie Hellman key exchange protocol and RSA encryption scheme. You will explore the properties of these schemes, and see how naive implementations can lead to insecurity. You will also learn to use GPG, a commonly used set of cryptographic tools used for secure communication. Environment. You are free to implement the solutions to this lab using the programming language and cryptographic library of your choosing. However, the instructor's strong recommendation is that you use Python and PyCrypto (or some other high-level language with decent crypto support) Task I. Implement Diffie Hellman Key Exchange The goal of this task is to get your public key crypto juices flowing by implementing one of the single most important discoveries in modern cryptography: the Diffie Hellman Key Exchange. In a single program, emulate the followin g protocol Alice Bob Privately Computes Sends Privately Computes Sends P.g Pick random element a e Pick random element b S A-g mod p B g mod p sA mod p k SHA256(s) m, "Hi Alice! k SHA256(s) m"Hi Bob!" CAES-CBC,(mo) C1-AES-CBC.(m.) Try it in a small group first, setting p- 37 and g 5. Confirm Alice and Bob compute the same symmetric key k. Truncate the output of SHA256 to 16 bytes, so that you can use it to AES-CBC encrypt some messages between Alice and Bob A. Modify your implementation from Task I in the following way: Alice Mallory Bob Computes Sends Modifies Computes Sends P,g A- g mod p B g mod p s Ab mod p k SHA256(s) m, "Hi Alice!" k SHA256(s) mo"Hi Bob!" CD Ci C,AES-CBC (m,) In your implementation, show that Mallory can successfully decrypt the messages c and c, B. Repeat this attack, but instead of tampering with A and B, tamper with the generator g. Show that Mallory can recover some of the messages by setting g to 1, p, or p-1 Why were these attacks possible? What is necessary to prevent them? Task IlI. Implement "textbook" RSA & MITM Key Fixing via Malleability From Diffie Hellman, we move to the next monumental breakthrough in public key cryptography RSA, named for its inventors: Rivest, Shamir and Adelman A. Let's implement it! RSA has two core components: key generation and encryption/decryption. (90% of the work is in implementing key generation.) Your implementation should support variable length primes (up to 2048 bits), and use the value e 65537. Feel free to use your cryptographic library's interface for generating large primes, but implement the rest-including computing the multiplicative inverse-yourself Encrypt and decrypt a few messages to yourself to make sure it works. Remember messages must be integers in You can convert an ASCIl string to hex, and then turn that hex value into an integer While it's very common for many people to share an e (common values are 3,7, 216+1), it is very bad if two people share an RSA modulus n. Briefly describe why this is, and what the ramifications are B. What you just implemented is often called "textbook" RSA, and it is wildly insecure. Because it is too slow and inconvenient to operate on a large amount data directly, RSA is often used to exchange a symmetric key that will be used to encrypt future messages. It would be terrible, of course, if an adversary were able to learn that key. And, that's what we're about to do One of textbook RSA's great weaknesses is its malleability, i.e. an active attacker can change the meaning of the plaintext message by performing an operation on the respective ciphertext. To demonstrate the dangers of malleability, implement the following protocol Alice Mallory Bob Computes SendsModifies Computes Sends n,e S E k SHA256(s) m "Hi Bob!" co AES-CBC.(m) C3 Find the operation F) that Mallory needs to apply to the ciphertext c that will allow her to decrypt the ciphertext c HINT: Mallory knows Alice's public key (n,e) and can encrypt her own messages to Alice Give another example of how RSA's malleability could be used to exploit a system (e.g. to cause confusion, disruption, or violate integrity Malleability can also affect signature schemes based on RSA. Consider the scheme Sign(m,d) m mod n Suppose Mallory sees the signatures for two message m, and m2 Show how Mallory can create a valid signature for a third message, m-m, m,2. C. Forward Secrecy (sometimes called Perfect Forward Secrecy) is a property of key-agreement protocols that ensures that all prior communications encrypted with a symmetric session key derived from a long-term private key, will still remain secure, even if the private key becomes compromised. However, not all key exchange protocols exhibit forward secrecy. Briefly justify whether either of the following key exchange protocols do or do not provide forward secrecy HINT: You need not worry about active adversaries (i.e. man-in-the-middle or message tampering attacks). Instead, consider only an eavesdropping adversary that keeps a transcript of all traffic between Alice and Bob, but may later be able to compel Alice or Bob to give up their secrets Alice Bob Privatle Computes Sends Privately Computes Sends p.g A g mod p B-g modp s B mod p Forget a k SHA256(s) m,-"Hi Bob!" s=A"mod p Forget b k = SHA256(s) m,"Hi Alice!" c, AES-CBC.(m) Co C1 e AES-CBC (m) Protocol 1: A Diffie-Hellman key-agreement Alice Bob Privately Computes Sends Privately Computes Sends RSA key pair Agub.pn? Pick random element x , x- RSA (Api. y) k SHA256x) k SHA256(x) Mg-"Hi Bob!" cAES-CBC,(m) m, "Hi Alice!" c, AES-CBC (m,) Protocol 2: An RSA key exchange Task IV. GPG: A Real Life Public Key Crypto Tool For this task, you will generate your own GNU Privacy Guard (GPG) public key pair using Keybase. Before Keybase came along, most users used the command line interface to GPG This web tutorial along with GPG's MiniHOWTO might show you how bad that actually is A. If you don't already have a public key, visit https://keybase.io, create an account, and generate a public key pair for yourself. Feel free to use the default parameters, or play with them as you see fit. If possible, verify yourself using a few methods. The idea being: the more methods authenticated methods you use, the more trust you build in the authenticity of your key B. Now, join the web of trust by "following" some of your friends, classmates, or me. Optionally you can use an HKP server, such as keys.gnupg.net, to publish and exchange keys. Be sure to verify the identity of the owner and key before signing it. Verifying the key's fingerprint with the owner over a "secure" or out-of-band channel (e.g. face-to-face, over the phone, or by trusting keybase's authentication techniques) is an easy way to do this C. Finally, encrypt and sign a message to Prof. Peterson and publish it as a plaintext attachment to the Secret Message discussion topic within the CPE321 Student Forum on PolyLearn. Feel free to use keybase's web or command-line interface to do this. For verification here is his key fingerprint: BC57A618547771A977BFBD14F94EFBEODSE6E6CB D. (Optional) If you don't want to use your key anymore you can destroy your keybase account. Task V. While the features provided by public key cryptography are attractive, they come at the cost of performance. In this task, you will quantify the performance differences between public and symmetric key algorithms. Fortunately, OpenSSL provides a simple interface for doing so openssl speed rsa and openssl speed aes will perform and measure their respective public and symmetric key operations using different parameters. One of the returned results for both operations is a measure of throughput operations per time (e.g. signatures per second). Run these operations and report your findings. Include two graphs: one that plots the block size vs. throughput for the various AES
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


