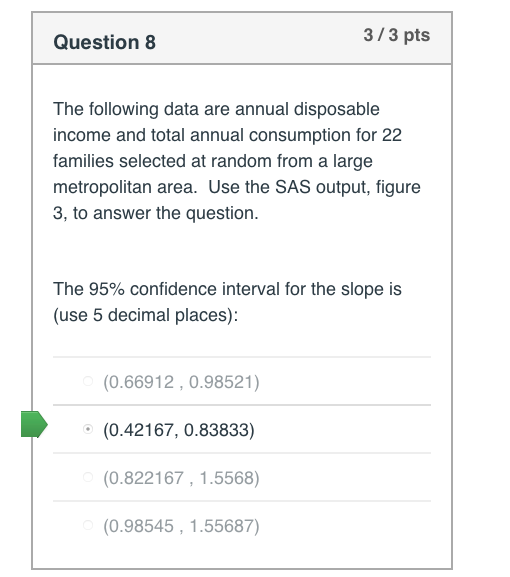
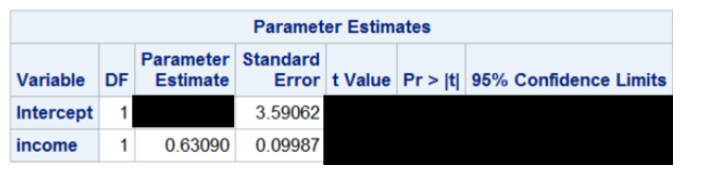
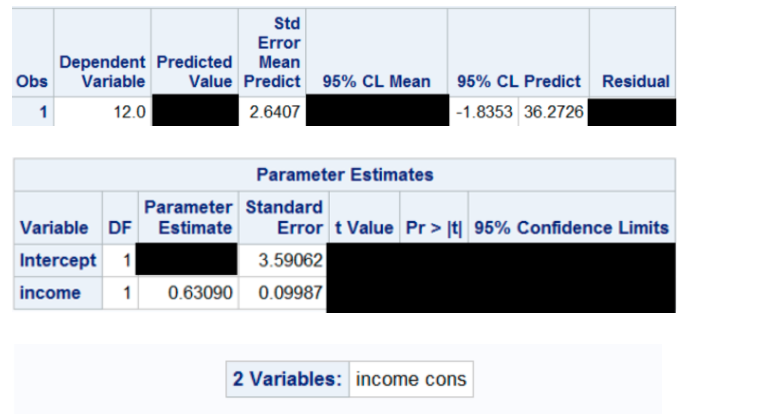
!HI EXPERT PLEASE HELP

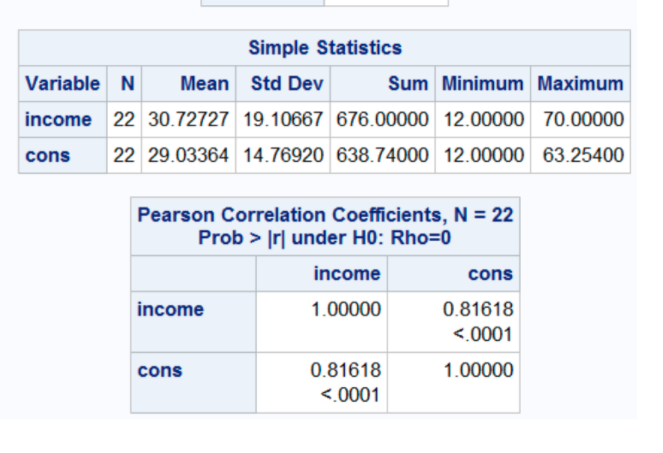
Question 1 Consider a one-period economy with a single representative consumer, a sin- gle representative firm and the government. The representative consumer derives utility from consumption c and leisure I: u (c, !) = Inc + In/ (1) The firm produces output Y using capital K and labor N according to Y = =KN1-a (2) where z is the total factor productivity and a is the Cobb-Douglas parameter. The firm maximizes profits # which are then transferred to the representative consumer. The government balances the budget using lump-sum taxes T on the repre- sentative consumer to finance government spending G. The hourly wage in this economy is w and the consumer has h hours to divide between leisure and labor. (i) Write down the consumer's budget constraint and the firm's profits function. (05 marks) (ii) Assume that w = 10, = = 20, a = 0.3, and K = 1. Calculate the number of hours that the firm would like to hire and the profits of the representative firm. (05 marks) (iii) Assume that government spending G is 10, the representative consumer receives the profits that you calculated above and earns hourly wage w = 10. Calculate how many hours of work the representative con- sumer would like to supply in the market. (10 marks) (iv) In the economy described above, (i) the government budget is balanced, (ii) the representative consumer maximizes lifetime utility given the budget constraint and w, and (iii) the firm maximizes profits given the production function and w. Is this a competitive equilibrium? Why or why not? (05 marks) Total: 25 marksQuestion 8 3/3 pts The following data are annual disposable income and total annual consumption for 22 families selected at random from a large metropolitan area. Use the SAS output, figure 3, to answer the question. The 95% confidence interval for the slope is (use 5 decimal places): O (0.66912 , 0.98521) (0.42167, 0.83833) O (0.822167 , 1.5568) O (0.98545 , 1.55687)Parameter Estimates Parameter Standard Variable DF Estimate Error t Value Pr > |t| 95% Confidence Limits Intercept 3.59062 income 0.63090 0.09987Use information from the SAS output (fig. 4} The following data are annual disposable inoome and total annual oonsumption for 22 families selected at random from a large metropolitan area. Use all decimals for ealoulations and 2 decimal places for your final answer. The 95% CI for a oonditional mean of income { 2mm} is equal to 12 {or 1 st observation in figure 4}: 95% Cl (21129.80: 27132.20} 05% Cl {300?5.00; 4?0?2.20} 05% Cl {24560003027620} * 95% Cl (11.?0, 22.?2] Std Error Dependent Predicted Mean Obs Variable Value Predict 95% CL Mean 95% CL Predict Residual 12.0 2.6407 -1.8353 36.2726 Parameter Estimates Parameter Standard Variable DF Estimate Error t Value Pr > |t| 95% Confidence Limits Intercept 3.59062 income 0.63090 0.09987 2 Variables: income cons