










Hi! Giving awesome review for correctness and good work!! Preferably typed in a document or eligible handwriting!!
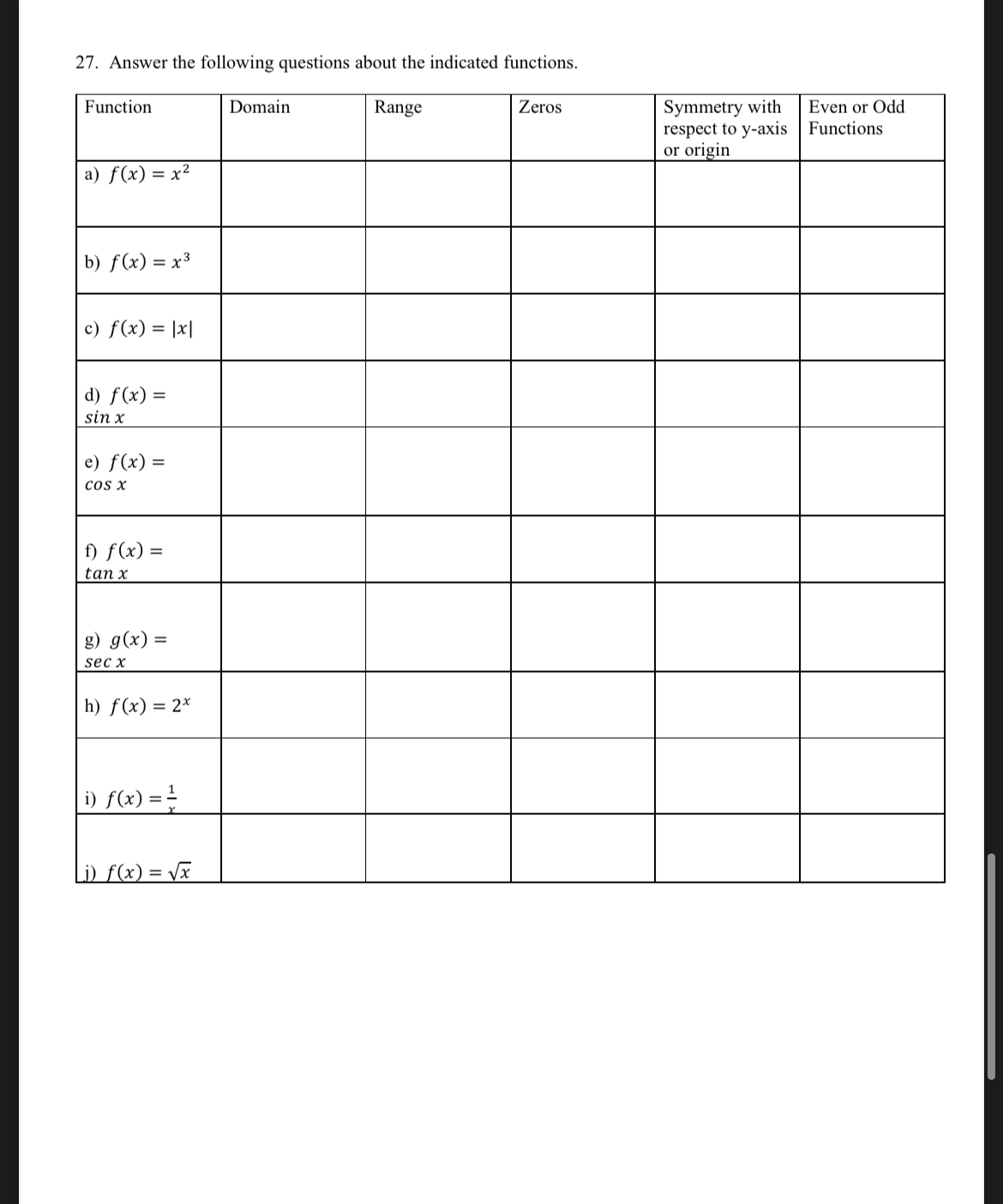
\f7. Find an equation of the vertical line with x-intercept at 3 8. Sketch a graph of the equation. a)y=3 b)y2=(x1) 9. Write the general forms of the equations of the lines through the point a) parallel to the given line and b) perpendicular to the given line. a) point: (-7, -2) line: x=l b) point: (2, 1) line: 4x2y = 3 10. Evaluate (if possible) the function at the given value(s) of the independent variable. Simplify the results. a) For f(x)= 52:: mm [(0). mi). f(2). ftx-l) b) For f(x) = x3, nd _f(x+&:;-f(:c) 1 . 1 1 1 3'7. Findthesum. 1;+;+.... 38. Find the sum Sin 7(3)"- 1 1 39. Find the first four partial sums and the nth partial sum of the sequence an: m E 40. Write the sum using sigma notation: 1 2x + 3x2 413:3 + 5x4+. . . . 100:!69'J 41. Find the nth term of a sequence whose first several terms are given. a) 1,3,i,,.... b) 5,25,125,625,.... 3 9 42. Find the limits. 1 1 . x+12 . _ a) hm _ b) itmm x>3 x 3 x>D x . costam'} . x3+1 c) hm cl 11m 3H] 1'} x>1 1+1 c) y=x3. y =1: 4) Determine whether the statement is true or false. If it is false, explain why or given an example that shows it is false. a) If (-4, -5) is a point on a graph that is symmetric with respect to the x-axis, then (4, -5) is also a point on the graph. b) If (-4, -5) is a point on a graph that is symmetric with respect to the y-axis, then (4, -5) is also a point on the graph. c) If the discriminant in a quadratic equation is greater than zero, then the graph of the quadratic has two 1(- intercepts. d) If the discriminant in a quadratic equation equals zero, then the graph of the quadratic has only one x- intercept. 5. Find an equation of the line that passes through the point and has the indicated slope. a) (0,3) slope-=3 b) (3, -2) m = 3 6. Find an equation of the line that passes through the points and sketch the line. 3) (2,8)and(5. 0) b) (6. 3) 3116105. 8) 15. Given f(x) = and g(x) = x2 1, nd each: a) f(9(1)) 13) QUCID C) U(x)) 16. Given f(x) = sin x and 30:) = xx, evaluate each expression: a) f(9(2)) b) SUCOD C) KM\") 1?. Factor and simplify. Express the answer as a fraction without negative exponents. 1 1 3x(2x + 5)? + 3(2x + 5)? 18. Express as a simpler fraction 4-1 2(x+h) 2x 31. Convert the rectangular equation to polar form: x2 + y2 = 9 32. Convert the polar equation to rectangular form: r = 3sine 33. Sketch a graph: r = 2 - 5cose 34. Sketch a graph: r = 2sin30 35. Determine whether the infinite geometric series is convergent or divergent. If it is convergent, find its sum. a) 1 - -+4 -2+... b) 1 - V2 + 2 - 2V2 + 4-... 36. Determine the nth term of the geometric sequence. a) -8, -2, -=, --,... b) t, 2 5, 2 ,....DIRECTIONS: Solve each problem below. Write neatly. Show all work. Box in your nal answers. 1. Test for Symmetry with respect to each axis and to the origin. a)y=x26 b)y=x2x+1 2) Sketch the graph of the equation. Identify any intercepts and test for symmetry a)y=23x b)y=9:r2 C)J'=X3+2 d)}'=6-IX| 3. Find the points of intersection of the graphs of the equations. a) x+y=8,4xy=7 b) x2+y=6,x+y=4 23. Use the properties of logarithms to expand the expression (3x2 + 2) vx+8 In - (x - 1)4 24. Solve for x In x - In (x - 1) =1 25. Find all 0 in the interval [0, 27] that satisfy the equations: sin 20 = = 26. Simplify secsec 0 tantan 0l3. Sketch a graph of the function and state its domain and range. a) h(x)=\\ix6 b) f(:r)=\\/'5'x2 c) g(t) = 35in art 14. Use the graph of y = f (x) to match the function with its graph: y=f(x+5), y=f(x)5, y=f(x)2, y=f(x4), y=f(x+6)+2, y=f(x1)+3 I 28. Sketch the curve represented by the parametric equations using a calculator and write teh corresponding rectangular equation by eliminating the parameter. a. x=2t+3, y=3t+1 b.x=t+1,y=t2 c. x=\\/E,y=t+5 d. x = 3cost, y = 45in: 29. Convert from polar to rectangular form: a. (an/3) b. (2, Sir/3) 30. Convert from rectangular to polar form a. (3, 4) b. (3, 4E) c) For f (x) = cos 2x, find f(0), f (-"), f(") d) For f (x) =, find (2)-f(2) x-2 11. Find the domain of the function a) f(x) = V6x b) y = sec c) f (x) = = 12. Evaluate the function as indicated. Given f(x) = {lx| + 1,x






























