Hi! i need help on my school assignment which graded me very high % so ..... Wonder if anyone can help with this question with python.MUST BE PYTHON as i need to show the answer from python.

Question:

(b) Suppose that the stock price of a company X is currently USD 200, has a volatility of 30% and the prevailing risk-free rate is 2%. Find, by applying the Black-Scholes formula, the price of an at-the-money put option that matures in 3 months. Who in the financial market would quote an option price this way? (7 marks) (c) Suppose that the stock price of a company Y is currently USD 250, has a volatility of 25% and the prevailing risk-free rate is 2.5%. What is the hedging position in the stock for an option writer who has sold an at-the-money 6-month call option 3 months ago? (7 marks)

Example qns provided by my lecturer:

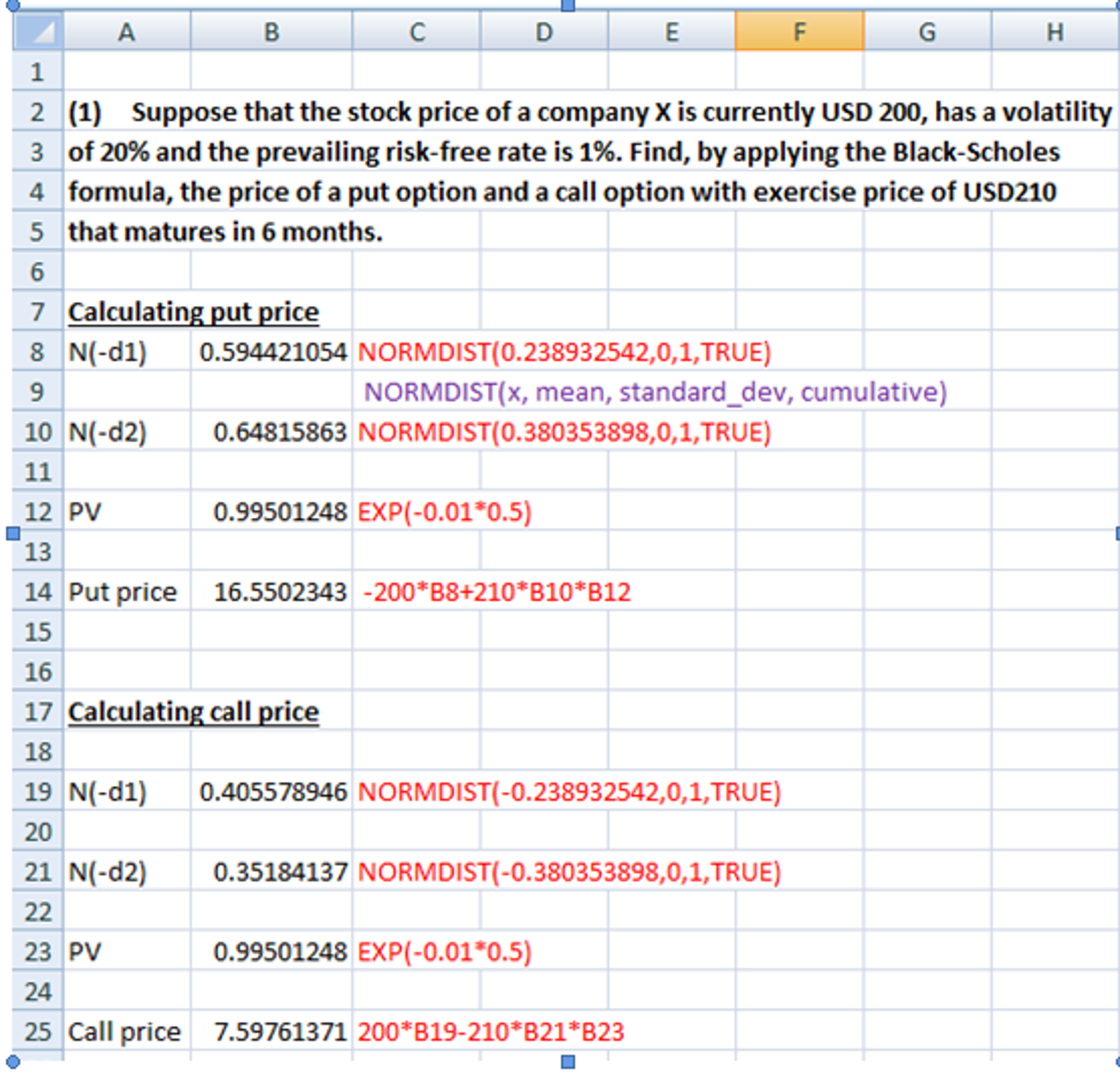
(1) Suppose that the stock price of a company X is currently USD 200, has a volatility of 20% and the prevailing risk-free rate is 1%. Find, by applying the Black-Scholes formula, the price of a put option and a call option with exercise price of USD210 that matures in 6 months.

In [1]: import math

In [2]: from scipy.stats import norm

In [3]: def d1(s, k, sigma, t, r):

...: x = (math.log(s * math.exp(r * t) / k) + 0.5 * sigma**2 * t) / (sigma * math.sqrt(t))

...: return x

...:

In [4]: def d2 (s, k, sigma, t, r):

...: x = (math.log(s * math.exp(r * t) / k) - 0.5 * sigma**2 * t) / (sigma * math.sqrt(t))

...: return x

...:

In [5]: def putprice (s, k, sigma, t, r):

...: x = - s * norm.cdf(-d1(s, k, sigma, t, r)) + k * math.exp(-r * t) * norm.cdf(-d2(s, k, sigma, t, r))

...: return x

...:

In [6]: print putprice (200, 210, 0.20, 6./12, 0.01)

16.5502343571

In [7]: def callprice (s, k, sigma, t, r):

...: x = s * norm.cdf(d1(s, k, sigma, t, r)) - k * math.exp(-r*t)*norm.cdf(d2(s, k, sigma, t, r))

...: return x

...:

In [8]: print callprice (200, 210, 0.20, 6./12, 0.01)

7.59761372661

(2) Suppose that the stock price of AAPL is currently USD 116, has a volatility of 20% and the prevailing risk-free rate is 1%. Find, by applying the Black-Scholes formula, the price of a put option and call option with exercise price of USD110 that matures in 2 months.

In [9]: print callprice(116, 110, 0.20, 2./12, 0.01)

7.5654180523

In [10]: print putprice (116, 110, 0.20, 2./12, 0.01)

1.3822374119

In [11]:

Formula workings:

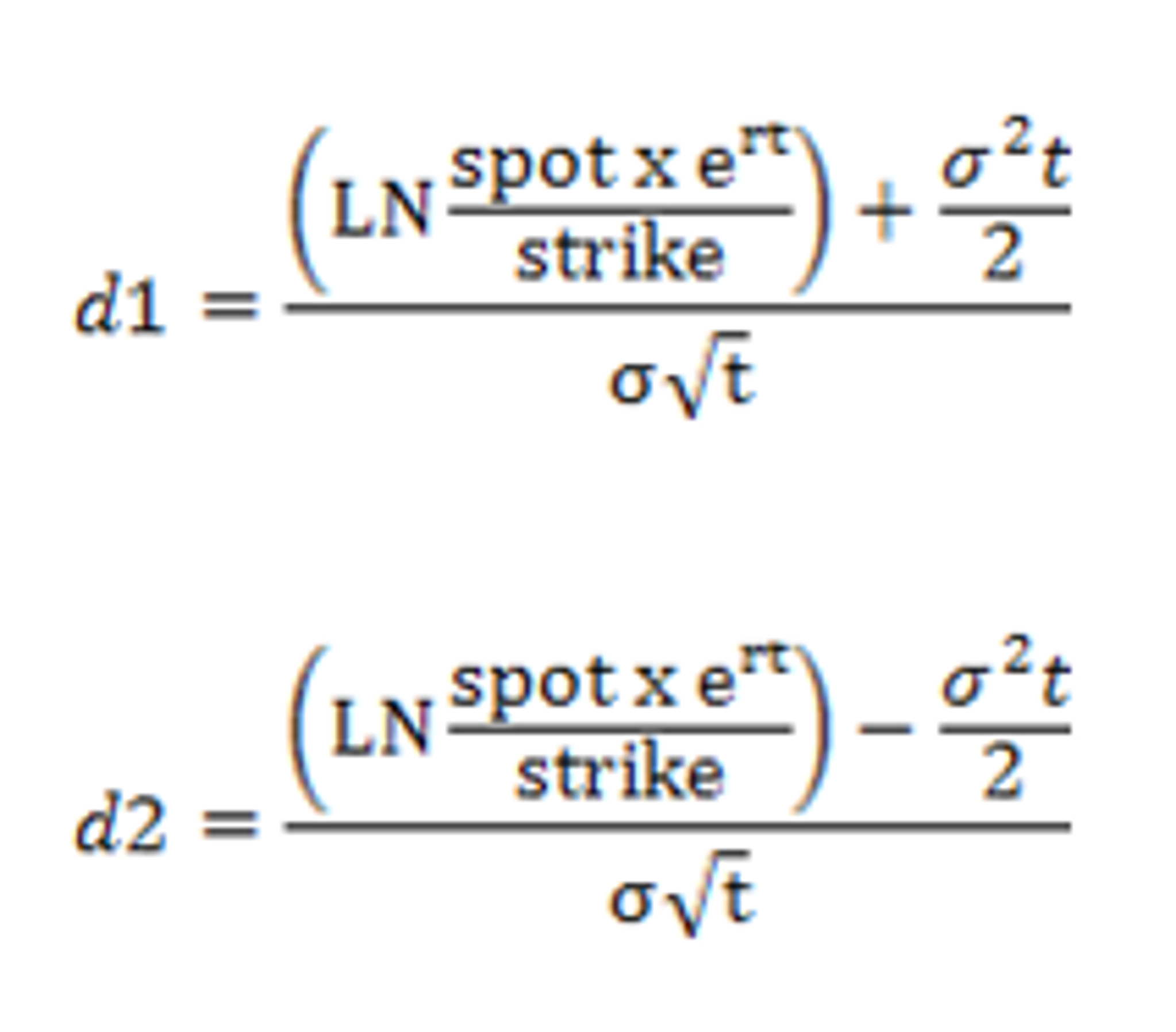
Call premium = spot price x N(d₁) strike price x N(d₂) x e^-rt

Put premium = - spot price x N(-d₁) + strike price x N(-d₂) x e^-rt

Put premium for Q1:

Put premium = - 200 x N(0.238932542) + 210 x N(0.380353898) x e^-0.01*0.5

Put premium = - 200 x 0.594421054 + 210 x 0.64815863 x e^-0.01*0.5

Put premium = 16.550234

Optional:

See Excel calculation below on how to find the cumulative distribution function.

(LN sstrikert)-T spot x e 2 03 spotx e strike LN d2 =