Hi. I need help with these, please!

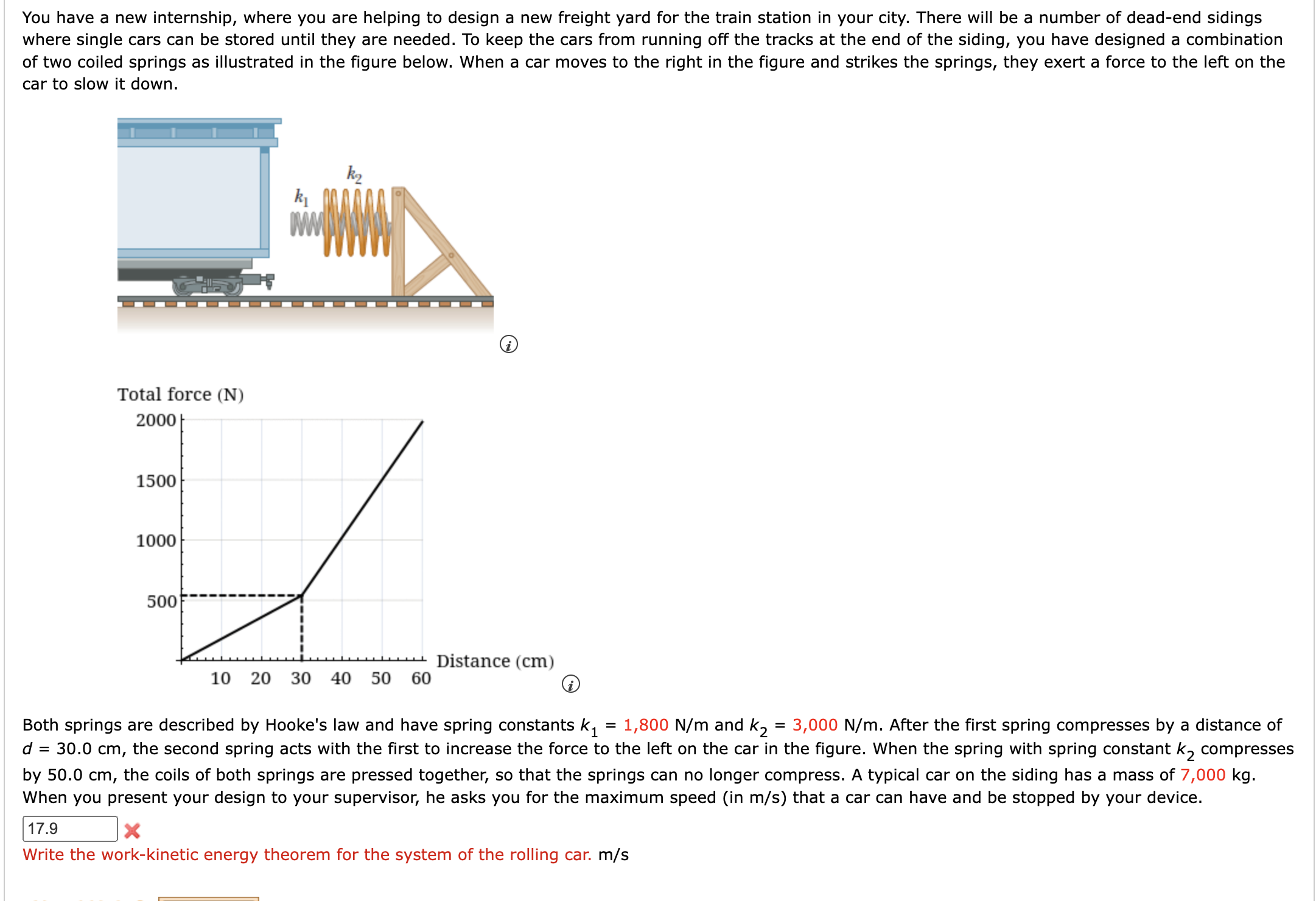
You have a new internship, where you are helping to design a new freight yard for the train station in your city. There will be a number of dead-end sidings where single cars can be stored until they are needed. To keep the cars from running off the tracks at the end of the siding, you have designed a combination of two coiled springs as illustrated in the figure below. When a car moves to the right in the figure and strikes the springs, they exert a force to the left on the car to slow it down. Total force (N) 2000 1500 1000 500 """""" Distance (cm) 10 20 30 40 50 60 (3 Both springs are described by Hooke's law and have spring constants k1 = 1,800 N/m and k2 = 3,000 N/m. After the first spring compresses by a distance of d = 30.0 cm, the second spring acts with the first to increase the force to the left on the car in the figure. When the spring with spring constant k2 compresses by 50.0 cm, the coils of both springs are pressed together, so that the springs can no longer compress. A typical car on the siding has a mass of 7,000 kg. When you present your design to your supervisor, he asks you for the maximum speed (in m/s) that a car can have and be stopped by your device. 17.9 x Write the work-kinetic energy theorem for the system of the rolling car. m/s A 1.20-kg object slides to the right on a surface having a coefficient of kinetic friction 0.250 (Figure a). The object has a speed of v; = 3.20 m/s when it makes contact with a light spring (Figure b) that has a force constant of 50.0 N/m. The object comes to rest after the spring has been compressed a distance d (Figure c). The object is then forced toward the left by the spring (Figure d) and continues to move in that direction beyond the spring's unstretched position. Finally, the object comes to rest a distance D to the left of the unstretched spring (Figure e). a m b d C V= 0 d O = A e (a) Find the distance of compression d (in m). 0.224 X You will find that you need to use the quadratic equation to find this distance. m (b) Find the speed v (in m/s) at the unstretched position when the object is moving to the left (Figure d). 2.84 X You appear to have correctly calculated the speed using your incorrect value from part (a). m/s (c) Find the distance D (in m) where the object comes to rest. 0.52 X This part is easiest to work by starting with your answer to part (b) (if it is correct!), but it can also be worked using only your answer to part (a). To understand how, think about the initial state of the system (object traveling with a speed 3.20, spring uncompressed) and the final state of the system (object at rest, spring uncompressed). What happens to the kinetic energy of the object? m (d) What If? If the object becomes attached securely to the end of the spring when it makes contact, what is the new value of the distance D (in m) at which the object will come to rest after moving to the left? 0.107 X m(a) A 15.0 kg block is released from rest at point A in the figure below. The track is frictionless except for the portion between points B and C, which has a length of 6.00 m. The block travels down the track, hits a spring of force constant 2,300 N/m, and compresses the spring 0.200 m from its equilibrium position before coming to rest momentarily. Determine the coefficient of kinetic friction between the block and the rough surface between points B and C. 3.00 m B -6.00 m C 0.546 X You appear to have used the wrong sign for the some of the energy terms. Think carefully about what terms correspond to the initial mechanical energy and the final mechanical energy. (b) What If? The spring now expands, forcing the block back to the left. Does the block reach point B? O Yes O No If the block does reach point B, how far up the curved portion of the track does it reach, and if it does not, how far short of point B does the block come to a stop? (Enter your answer in m.) 6.505 x mYou are working with a team that is designing a new roller coaster-type amusement park ride for a major theme park. You are present for the testing of the ride, in which an empty 150 kg car is sent along the entire ride. Near the end of the ride, the car is at near rest at the top of a 104 m tall track. It then enters a nal section, rolling down an undulating hill to ground level. The total length of track for this nal section from the top to the ground is 250 m. For the first 230 m, a constant friction force of 350 N acts from computer-controlled brakes. For the last 20 m, which is horizontal at ground level, the computer increases the friction force to a value required for the speed to be reduced to zero just as the car arrives at the point on the track at which the passengers exit. (a) (b) (d) (8) Determine the required constant friction force (in N) for the last 20 rn for the empty test car. :1\" Find the highest speed (in m/s) reached by the car during the final section of track length 250 m. :l m You are asked by your team supervisor to determine the answers to parts (a) and (b) for a fully loaded car with an upper limit of 450 kg of passenger mass. Find these new values. (Give the friction force in N and the speed in m/s. Round the friction force to at least three significant figures.) friction force for last 20 m \\:] N highest speed reached m/s The required friction force in part (c) is well within design limits. The fastest speed, however, is well below that of current leading rides, so you would like to increase the maximum speed, You can't make the tower taller above ground, so you decide to include a feature where part of the track goes underground. Determine the depth (in m) to which the underground part of the ride must go to increase the maximum speed to 53.0 m/s. Assume the overall length of the first part of the track remains at 230 m and the length of track from the top to the lowest underground point is 150 m. The same 350 N friction force acts on the entire 230 m section of track. :lm Is the construction in part (d) feasible? 0 Yes, there is enough track both for the depth requirement to be satised and for the horizontal displacement of the length of track from the top to the lowest underground point to be of the same order of magnitude as its height. 0 No, there is not enough track both for the depth requirement to be satisfied and for the horizontal displacement of the length of track from the top to the lowest underground point to be of the same order of magnitude as its height