Hi i need to help to see if i answered these questions correct thank you

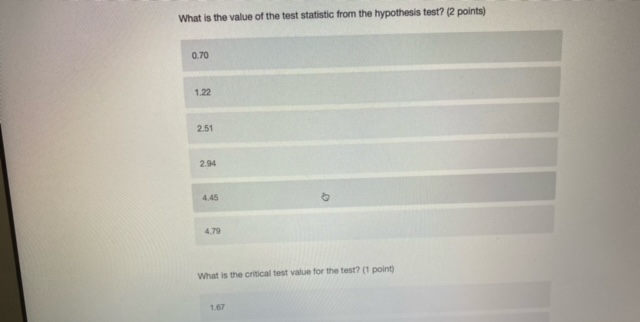
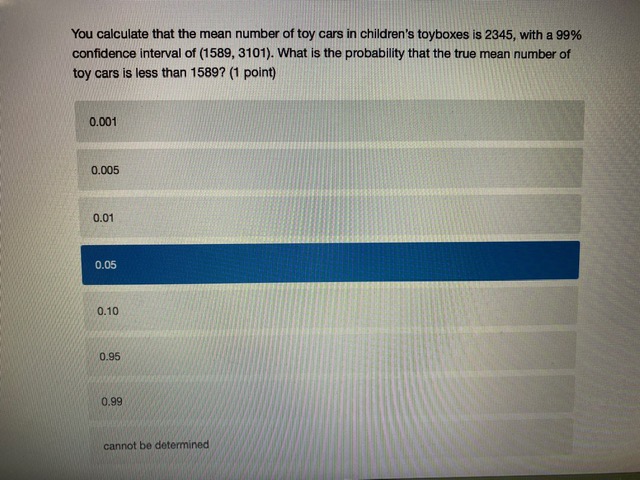
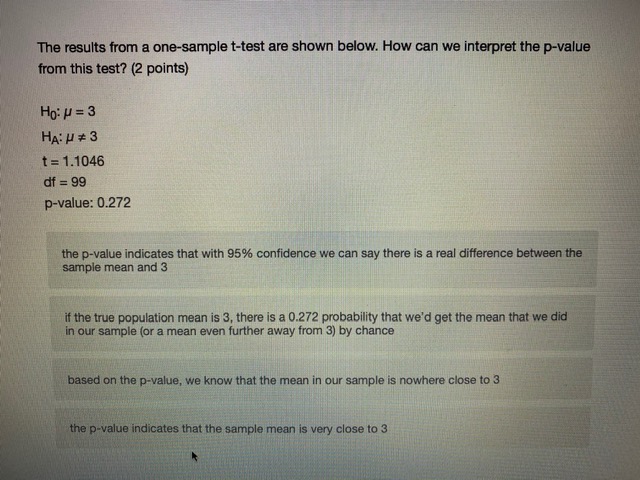
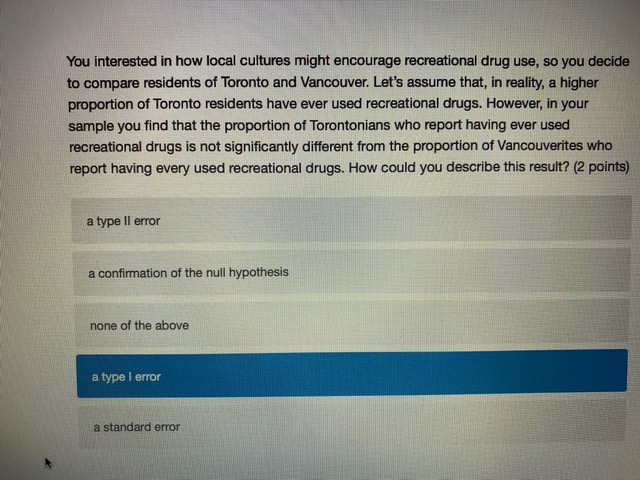
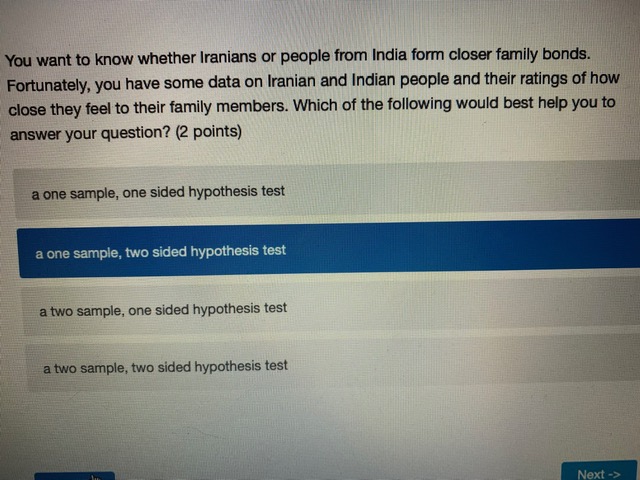
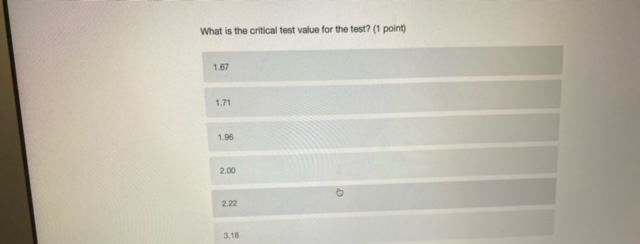
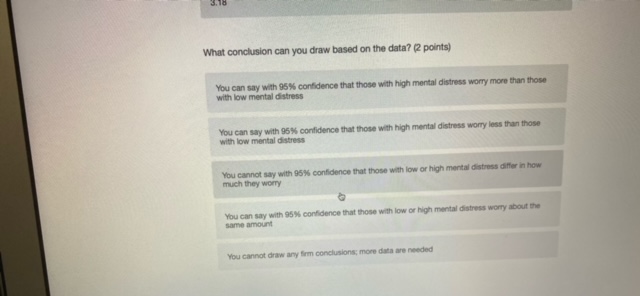
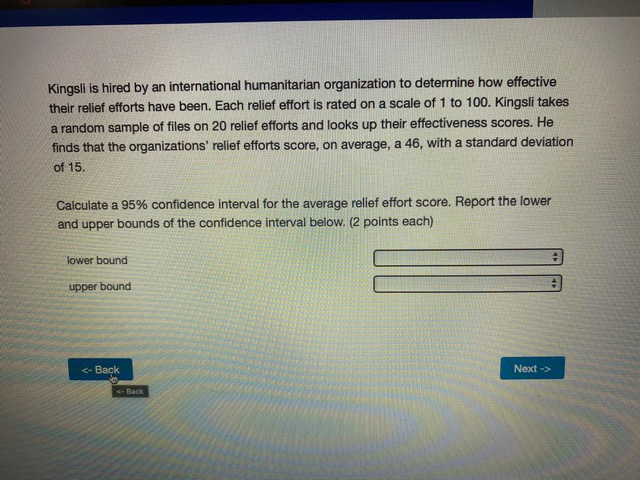
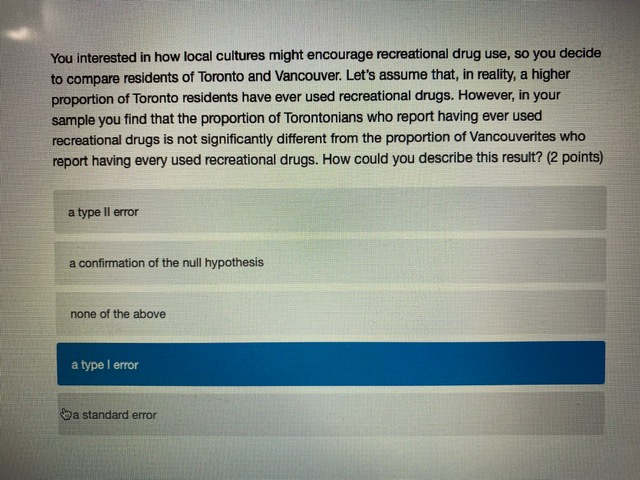
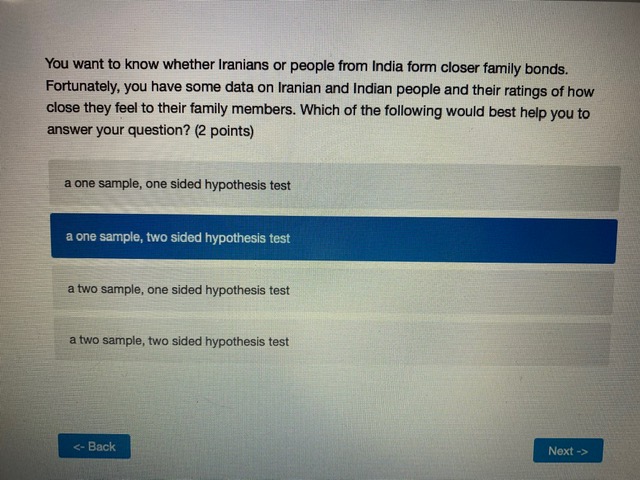
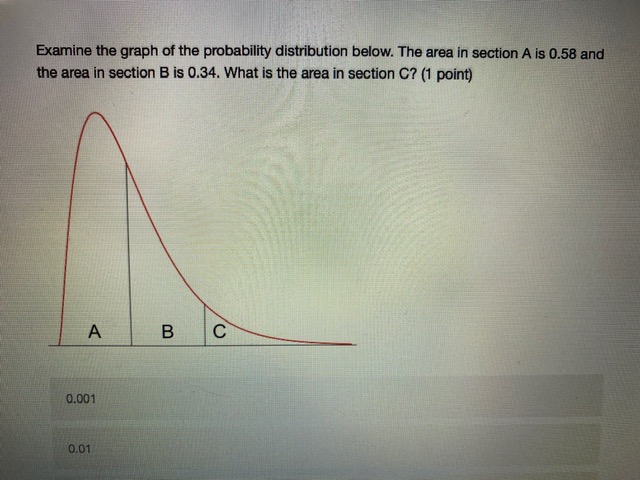
Chisonga randomly samples 60 people, and finds that 18 respondents report high mental distress, while the other 42 report low mental distress. He wants to know if respondents with high mental distress differ in how much they worry compared to those with low mental distress. To test this, he counts the number of worrying thoughts reported by Individuals in both groups. Descriptive statistics for those with low and high mental distress are shown in the table below. ow mental high mental distress distress average # worrying thoughts 33 49 standard deviation of 10.3 22.1 worrying thoughts N 42 18 Perform a hypothesis test to determine whether respondent with low and high levels of mental distress differ in the number of worrying thoughts they have (use an alpha level of 0.05).What is the value of the test statistic from the hypothesis test? (2 points) 0.70 1.22 2.51 294 4.45 4.79 What is the critical test value for the test? (1 point)\fYou calculate that the mean number of toy cars in children's toyboxes is 2345, with a 99% confidence interval of (1589, 3101). What is the probability that the true mean number of toy cars is less than 15897 (1 point) 0.001 0.005 0.01 0.05 0.10 0.95 0.99 cannot be determinedThe results from a one-sample t-test are shown below. How can we interpret the p-value from this test? (2 points) Ho: H = 3 HA: H # 3 t = 1.1046 df = 99 p-value: 0.272 the p-value indicates that with 95% confidence we can say there is a real difference between the sample mean and 3 if the true population mean is 3, there is a 0.272 probability that we'd get the mean that we did in our sample (or a mean even further away from 3) by chance based on the p-value, we know that the mean in our sample is nowhere close to 3 the p-value indicates that the sample mean is very close to 3You interested in how local cultures might encourage recreational drug use, so you decide to compare residents of Toronto and Vancouver. Let's assume that, in reality, a higher proportion of Toronto residents have ever used recreational drugs. However, in your sample you find that the proportion of Torontonians who report having ever used recreational drugs is not significantly different from the proportion of Vancouverites who report having every used recreational drugs. How could you describe this result? (2 points) a type ll error a confirmation of the null hypothesis none of the above a type I error a standard errorYou want to know whether Iranians or people from India form closer family bonds. Fortunately, you have some data on Iranian and Indian people and their ratings of how close they feel to their family members. Which of the following would best help you to answer your question? (2 points) a one sample, one sided hypothesis test a one sample, two sided hypothesis test a two sample, one sided hypothesis test a two sample, two sided hypothesis test Next ->\fWhat conclusion can you draw based on the data? (2 points) You can say with 95% confidence that those with high mental distress worry more than those with low mental distress You can say with 95% confidence that those with high mental distress worry less than those with low mental distress You cannot say with 95% confidence that those with low or high mental distress differ in how much they worry You can say with 95% confidence that those with low or high mental distress worry about the Sama amount You cannot draw any firm conclusions; more data are neededKingsli is hired by an international humanitarian organization to determine how effective their relief efforts have been. Each relief effort is rated on a scale of 1 to 100. Kingsli takes a random sample of files on 20 relief efforts and looks up their effectiveness scores. He finds that the organizations' relief efforts score, on average, a 46, with a standard deviation of 15. Calculate a 95% confidence interval for the average relief effort score. Report the lower and upper bounds of the confidence interval below. 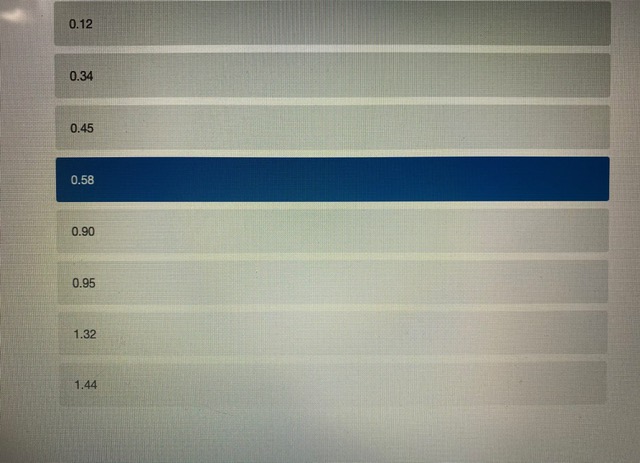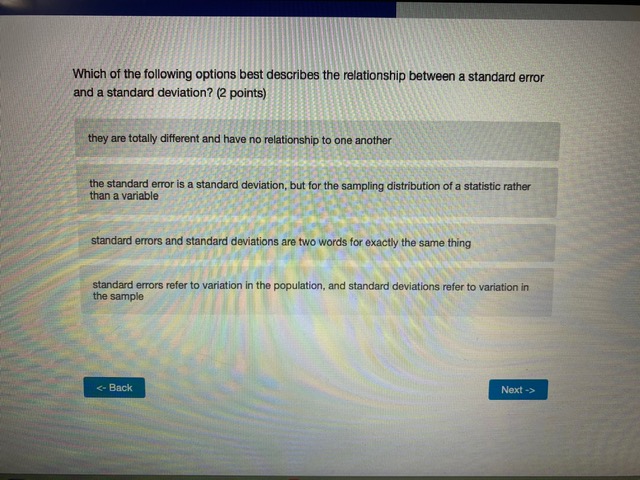(2 points each) lower bound upper bound - BackWhich of the following options best describes the relationship between a standard error and a standard deviation? (2 points) they are totally different and have no relationship to one another the standard error is a standard deviation, but for the sampling distribution of a statistic rather than a variable standard errors and standard deviations are two words for exactly the same thing standard errors refer to variation in the population, and standard deviations refer to variation in the sample You interested in how local cultures might encourage recreational drug use, so you decide to compare residents of Toronto and Vancouver. Let's assume that, in reality, a higher proportion of Toronto residents have ever used recreational drugs. However, in your sample you find that the proportion of Torontonians who report having ever used recreational drugs is not significantly different from the proportion of Vancouverites who report having every used recreational drugs. How could you describe this result? (2 points) a type ll error a confirmation of the null hypothesis none of the above a type | error @a standard errorYou want to know whether Iranians or people from India form closer family bonds. Fortunately, you have some data on Iranian and Indian people and their ratings of how close they feel to their family members. Which of the following would best help you to answer your question? (2 points) a one sample, one sided hypothesis test a one sample, two sided hypothesis test a two sample, one sided hypothesis test a two sample, two sided hypothesis test Examine the graph of the probability distribution below. The area in section A is 0.58 and the area in section B is 0.34. What is the area in section C? (1 point) A B C 0.001 0.01\f