Hi. Kindly help me solve these

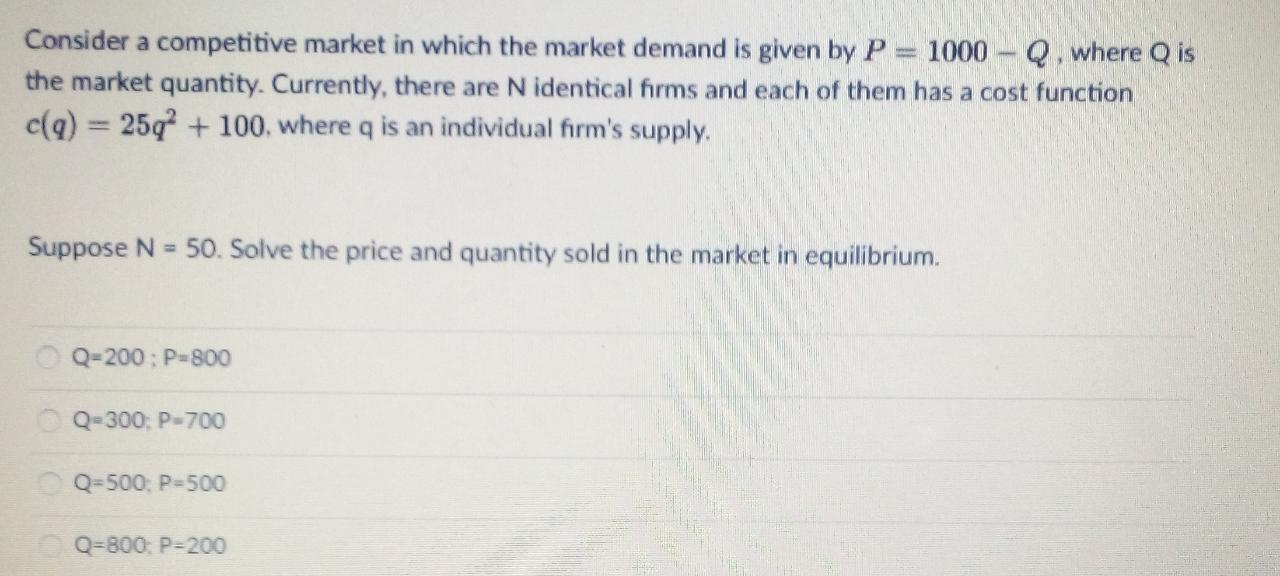
Consider a competitive market in which the market demand is given by P = 1000 - Q , where Q is the market quantity. Currently, there are N identical firms and each of them has a cost function c(q) = 25q + 100, where q is an individual firm's supply. Suppose N = 50. Solve the price and quantity sold in the market in equilibrium. Q-200 ; P=800 Q-300; P-700 Q-500; P=500 Q=800; P-200A perfectly competitive firm has a Cobb-Douglas production function f (X1, X2) = X,X2- Suppose that input prices are W, = 1 and W2 = 1. The firm wants to find the cheapest way of producing y = 32. a. Suppose that in the short run the quantity of input factor 2 is fixed at X2 = 8. Solve the firm's short-run cost minimization problem to derive the optimal input quantity xi . b. Derive the corresponding costs Cs of producing y = 32 in the short run. c. Now consider the long run, in which both input factors are variable. Set up the Lagrangian function for this firm's long-run cost minimization problem. d. Derive the first-order conditions of the above long-run cost minimization problem. e. Solve the above first-order conditions to derive the optimal input quantities x, and X2. f. Derive the corresponding costs c' of producing y = 32 in the long run.11. Consider a competitive industry where the market demand is given by P = 50-Q. The marginal cost function is simply MC-Q. If the government imposes a tax of 10 rupees per unit of production of this good, the equilibrium market price will go up by a. zero rupees b. 10 rupees c. 20 rupees d. 5 rupeesConsider a market with two firms each selling an identical product and with identical costs of c(qi) = 12q2 i i= 1, 2 where qi is the output of firm i. The market demand is given by p(Q) = 20 - Q where q is the total market output, Q = q1 + q2. Each firm chooses its own output to maximize their own profit ("Cournot Competition"). Consider a market with two firms each selling an identical product and with identical costs of c(qi) = =9. i = 1,2 where qi is the output of firm i. The market demand is given by P(Q) = 20 - Q where q is the total market output, Q = q1 + 92. Each firm chooses its own output to maximize their own profit ("Cournot Competition"). (a) Write the profit for firm 1 in terms of its own output as well as the output of the other firm: 71 (91, 92). Write out the profit for firm 2 as well: 72(91 , 92). (b) Solve for the Cournot equilibrium quantities (output quantities where each firm is simultaneously producing its best response). What is the market price? e) Is the output efficient? Derive the efficient level of output and com- pute the deadweight loss from the Cournot equilibrium. (Hint: what is the perfectly competitive market quantity with the two firms act- ino as price fakers? What is the difference in total surplus resulting