Hi there I need help with these questions Also last question says find the profit $ round to the nearest cent
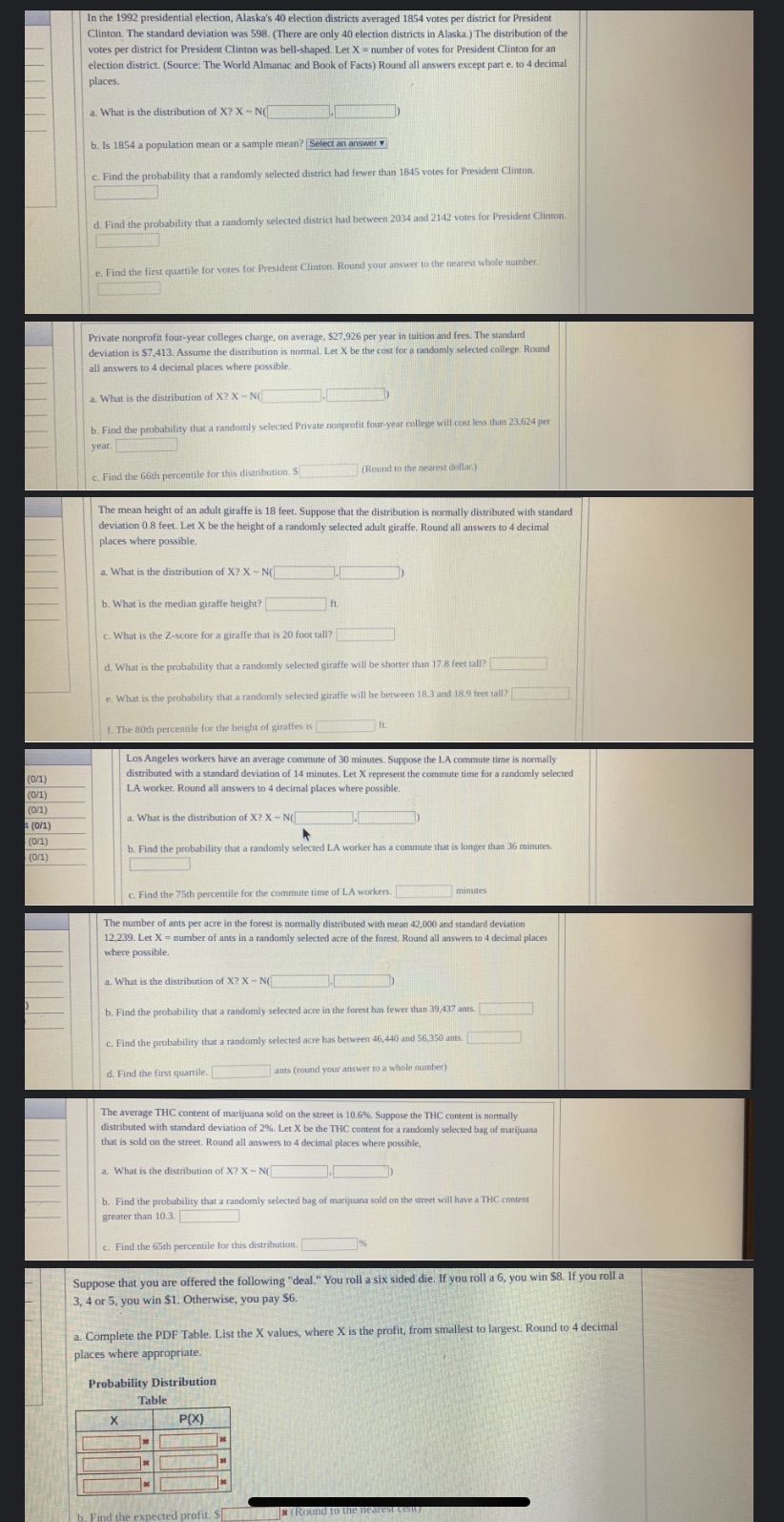
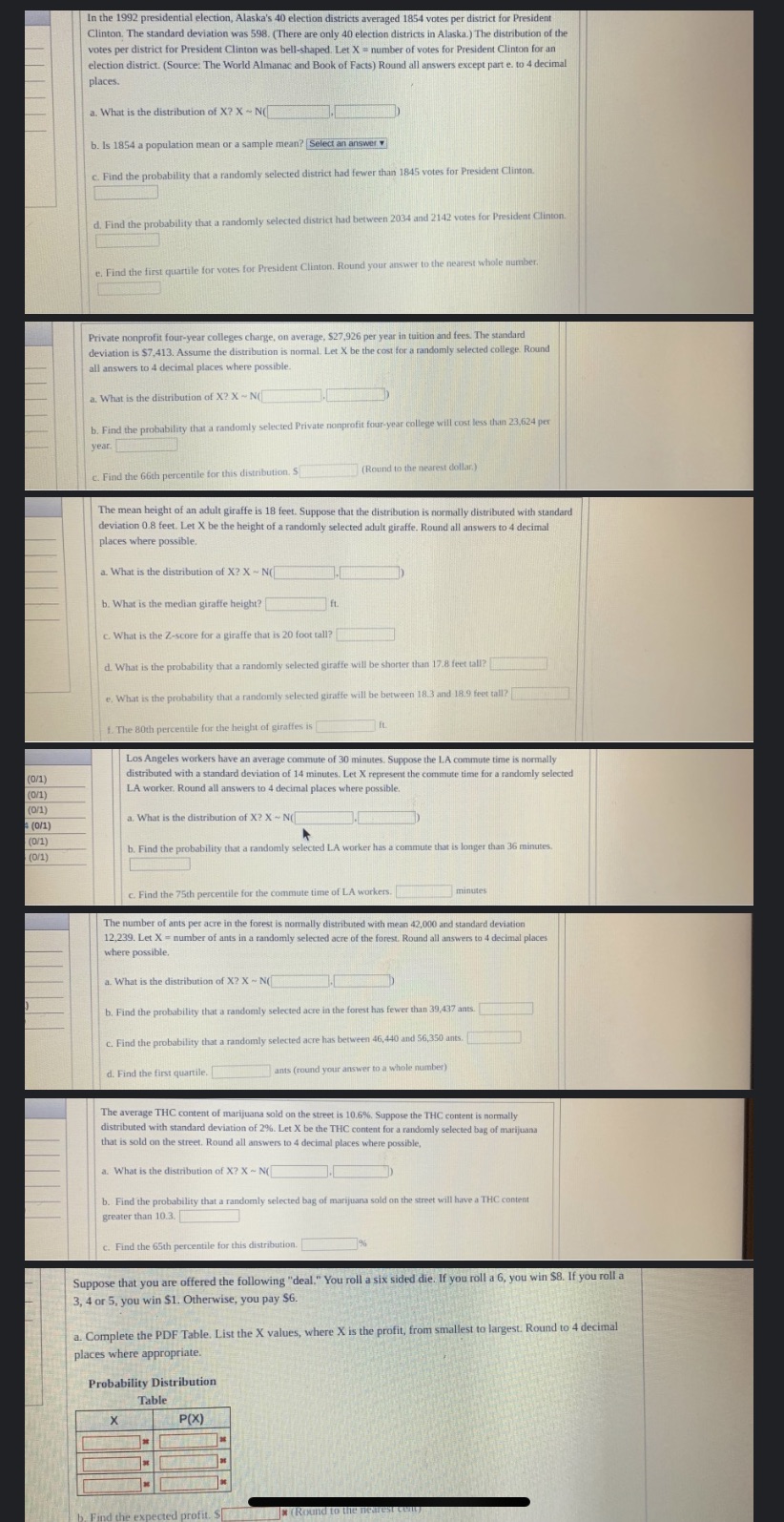
In the 1992 presidential election, Alaska's 40 election districts averaged 1854 votes per district for President Clinton. The standard deviation was 598. (There are only 40 election districts in Alaska.) The distribution of the votes per district for President Clinton was bell-shaped. Let X - number of votes for President Clinton for an election district. (Source: The World Almanac and Book of Facts) Round all answers except part e. to 4 decimal places. a. What is the distribution of X? X - N b. Is 1854 a population mean or a sample mean? [Select an answer c. Find the probability that a randomly selected district had fewer than 1845 votes for President Clinton. d. Find the probability that a randomly selected district had between 2034 and 2142 votes for President Clinton. e. Find the first quartile for votes for President Clinton, Round your answer to the nearest whole number, Private nonprofit four-year colleges charge, on average, $27,926 per year in tuition and fees. The standard deviation is $7,413. Assume the distribution is normal. Let X be the cost for a randomly selected college Round all answers to 4 decimal places where possible. a. What is the distribution of X? X ~ N b. Find the probability that a randomly selected Private nonprofit four-year college will cost less than 23,624 per year. c. Find the 66th percentile for this distribution. $ (Round to the nearest dollar.) The mean height of an adult giraffe is 18 feet. Suppose that the distribution is normally distributed with standard deviation 0.8 feet. Let X be the height of a randomly selected adult giraffe. Round all answers to 4 decimal places where possible. a. What is the distribution of X? X ~ N b. What is the median giraffe height? c. What is the Z-score for a giraffe that is 20 foot tall? d. What is the probability that a randomly selected giraffe will be shorter than 17.8 feet tall? e. What is the probability that a randomly selected giraffe will be between 18.3 and 18.9 feet tall? 1. The 80th percentile for the height of giraffes is Los Angeles workers have an average commute of 30 minutes. Suppose the LA commute time is normally (0/1 distributed with a standard deviation of 14 minutes. Let X represent the commute time for a randomly selected (0/1) LA worker. Round all answers to 4 decimal places where possible. (0/1) (0/1) a. What is the distribution of X? X - N (D/1) (0/1) b. Find the probability that a randomly selected LA worker has a commute that is longer than 36 minutes. c. Find the 75th percentile for the commute time of LA workers. minutes The number of ants per acre in the forest is normally distributed with mean 42,000 and standard deviation 12,239. Let X = number of ants in a randomly selected acre of the forest. Round all answers to 4 decimal places where possible, a. What is the distribution of X? X ~ N b. Find the probability that a randomly selected acre in the forest has fewer than 39,437 ants. c. Find the probability that a randomly selected acre has between 46, 440 and 56,350 ants. d. Find the first quartile. ants (round your answer to a whole number) The average THC content of marijuana sold on the street is 10.6%, Suppose the THC content is normally distributed with standard deviation of 2%. Let X be the THC content for a randomly selected bag of marijuana that is sold on the street, Round all answers to 4 decimal places where possible, a. What is the distribution of X? X ~ N b. Find the probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 10.3. C. Find the 65th percentile for this distribution. Suppose that you are offered the following "deal." You roll a six sided die. If you roll a 6, you win $8. If you roll a 3, 4 or 5, you win $1. Otherwise, you pay $6. a. Complete the PDF Table. List the X values, where X is the profit, from smallest to largest. Round to 4 decimal places where appropriate. Probability Distribution Table X P(X) profit. $ * (Round to the