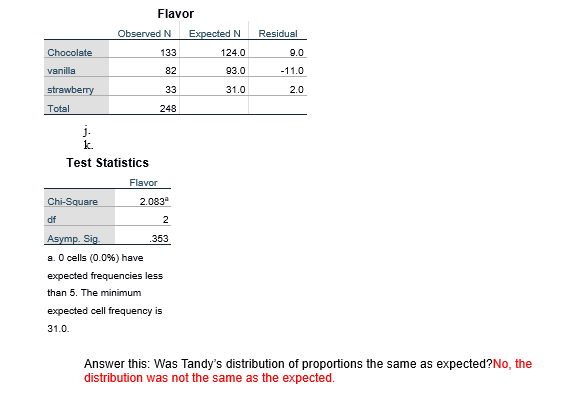
Hi there, my answers are in red. Can you please double check?

Problem Set 6.1: Critical Values Criterion: Explain changes in critical value based on calculations. Instructions: Read the following and answer the questions. The chi-sggare table. The degrees of freedom for a given test are listed in the column to the far left; the level of signicance is listed in the top row to the right. These are the only two values you need to nd the critical values for a chi-square test. Wort: through the tolowing exercise and write down what you see in the chi-smare table. This will help famiiarize you with the table. Increasing it and n. in the chi-square table 1. Record the critical values for a chi-square test, given the following values for it at each level of signicance: .16 .65 .61 it: 16 14.63 16.92 21.6? it = 16 22.31 25.66 36.53 it = 22 29.62 32.6? 33.93 it = 36 39.69 42.56 49.59 Note: Because there is only one .lrgiven, assume this is a goodnessrot-t test and com pute the degrees of freedom as [it 1]. 2. As the level of signicance increases [from .61 to .1 D), does the critical value increase or decrease? Decreases because the signicance level increases, which causes the condence level to decrease, then causes the CV to decrease. 3. As tr increases {from it] to so), does the critical value increase or decrease? Explain your answer as it relates to the test statistic The Elf ircreases, the possibility to reject the null decreases as It increases. Problem Set 3.2: Parametric Tests Criterion: Identityr parametric tests. Instructions: Based on the scale of measurement for the data, identify whether a test is parametric or nonparametric 1. A researcher measures the proportion of schizophrenic patients born in each season. Parametric A researcher measures the average age that schizophrenia is diagnosed among male and female patients. Parametric A researcher tests whether frequency of lntemet use and social interaction are independent. Non-Parametric A researcher measures the amount of time {in seconds} that a group of teenagers uses the lntemet tor school-related and non-school-related purposes. Nonparametric Problem Set 8.3: ChiSquare Analysis in SPSS Cn'terion: Use SPCS for a chi-square analysis. Data: Tandy's ioe cream shop serves chocolate, vanilla, and strawberry ice cream. Tandy wants to plan for the tuhlre years. She lmrrws that on average she experts to purchase till] cases of chocolate, 75 cases of vanilla, and 25 cases otstrawberry (4:3:1}. This year, the ice cream sales increased, and she purchased 133 cases of chocolate, 32 cases of vanila, and 33 cases of strawbeny. Instructions: Complete the following steps: a. b. F'F' Dpen SPSS and create a llew Data Set. Go to the Variable View tab and type Flavor in the st row and Frequency in the seoond rorw. Adjust the decimal value to it. Go to Values in the Flavor row and enter 1 for chocolate, 2 for vanila, and 3 for strawberry and cliclr DIE. Go to the Data View tab and under the Flavor column, enter 1 in row 1, 2 in row 2, and 3 it row 3. Under the fremency oolumn, enter 133 in row 1, 82 in row 2, and 33 in row 3. In the Toolbar, click Data, then select Weight Cases. Select Weight Cases By, select Frequency, and then ciclr Arrow to send it over to the Frequency Variable box. Click Cit] In the Toolbar, click Analyze, theerparametric Tests, then Legacy Dialogs, and then C iiiSquare. Select Flavor and then cliclc Arrow to send to the Test Variable List. Under Expected Values, select Values and then enter the following three values it the order 1oo, i5, and 25. Cliclr CH and copy and paste the output to the Word document. j.