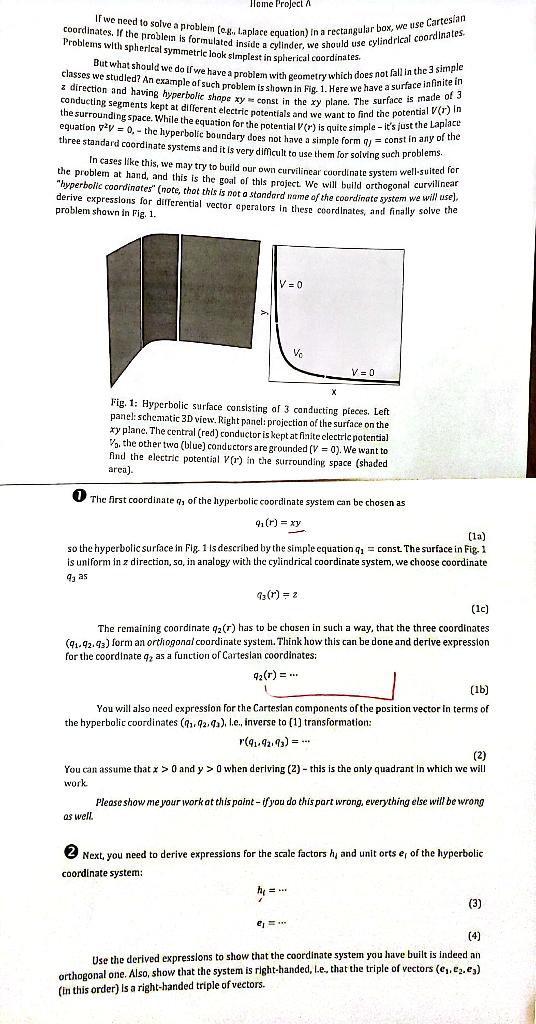
Home Project If we need to solve a problem (c.s., Laplace equation) in a rectangular box, we use Cartesian coordinates. If the problein is formulated inside a cylinder, we should use cylindrical coordinates But what should we do if we have a problem with geometry which does not fall in the 3 simple classes we studied? An example of such problem is shown in Fig. 1. Here we have a surface infinite in z direction and having hyperbolic shape xy const in the ry plane. The surface is made of 3 Problems with spherical symmetric look simplest in spherical coordinates. partie the surrounding space. While the equation for the potential (r) is quite simple it's just the Laplace equation F?v = 0, - the hyperbolic boundary does not have a simple forme = const in any of the three standard coordinate systems and it is very difficult to use them for solving such problems. In cases like this, we may try to build our own curvilinear coordinate system well-suited for the problem at hand, and this is the goal of this project. We will build orthogonal curvilincar "hyperbolic coordinates" (note, that this is not a standard name of the coordinate system we will use). derive expressions for diferential vector operators in these coordinates, and finally solve the problem shown in Fig. 1. V=0 V. V = 0 X Fig. 1: Hyperbolic surface consisting of 3 conducting pieces. Left panel: schematic 3D view. Right panel: projection of the surface on the xy plane. The central (red) conductor is kept at finite electric potential Vs the other two (blue) conductors are grounded (V = 0). We want to find the electric potential V(r) in the unding space (shaded area) The first coordinate , of the hyperbolic coordinate system can be chosen as 4.(r) = xy (la) so the hyperbolic surface in Fig 1 is described by the simple equation 41 = const The surface in Fig. 1 is uniform in z direction, sa, in analogy with the cylindrical coordinate system, we choose coordinate 4, as G(r) = 2 (1c) The remaining coordinate 42() has to be chosen in such a way, that the three coordinates (91.92.93) form an orthogonal coordinate system. Think how this can be done and derive expression for the coordinate 4, as a function of Cartesian coordinates: 92(r) = ... (1b) You will also need expression for the Cartesian components of the position vector in terms of the hyperbolic coordinates (1.02.02), l.e., inverse to (1) transformation: (01.42.0) = (2) You can assume that x > 0 and y > when deriving (2) - this is the only quadrant in which we will work Please show me your work at this point - if you do this part wrong, everything else will be wrong as well. Next, you need to derive expressions for the scale factors and unit orts e, of the hyperbolic coordinate system: he (3) e. (4) Use the derived expressions to show that the coordinate system you have built is indeed an orthogonal one. Also, show that the system is right-handed, l.e. that the triple of vectors (e, c.cz) (In this order) is a right-handed triple of vectors. Home Project If we need to solve a problem (c.s., Laplace equation) in a rectangular box, we use Cartesian coordinates. If the problein is formulated inside a cylinder, we should use cylindrical coordinates But what should we do if we have a problem with geometry which does not fall in the 3 simple classes we studied? An example of such problem is shown in Fig. 1. Here we have a surface infinite in z direction and having hyperbolic shape xy const in the ry plane. The surface is made of 3 Problems with spherical symmetric look simplest in spherical coordinates. partie the surrounding space. While the equation for the potential (r) is quite simple it's just the Laplace equation F?v = 0, - the hyperbolic boundary does not have a simple forme = const in any of the three standard coordinate systems and it is very difficult to use them for solving such problems. In cases like this, we may try to build our own curvilinear coordinate system well-suited for the problem at hand, and this is the goal of this project. We will build orthogonal curvilincar "hyperbolic coordinates" (note, that this is not a standard name of the coordinate system we will use). derive expressions for diferential vector operators in these coordinates, and finally solve the problem shown in Fig. 1. V=0 V. V = 0 X Fig. 1: Hyperbolic surface consisting of 3 conducting pieces. Left panel: schematic 3D view. Right panel: projection of the surface on the xy plane. The central (red) conductor is kept at finite electric potential Vs the other two (blue) conductors are grounded (V = 0). We want to find the electric potential V(r) in the unding space (shaded area) The first coordinate , of the hyperbolic coordinate system can be chosen as 4.(r) = xy (la) so the hyperbolic surface in Fig 1 is described by the simple equation 41 = const The surface in Fig. 1 is uniform in z direction, sa, in analogy with the cylindrical coordinate system, we choose coordinate 4, as G(r) = 2 (1c) The remaining coordinate 42() has to be chosen in such a way, that the three coordinates (91.92.93) form an orthogonal coordinate system. Think how this can be done and derive expression for the coordinate 4, as a function of Cartesian coordinates: 92(r) = ... (1b) You will also need expression for the Cartesian components of the position vector in terms of the hyperbolic coordinates (1.02.02), l.e., inverse to (1) transformation: (01.42.0) = (2) You can assume that x > 0 and y > when deriving (2) - this is the only quadrant in which we will work Please show me your work at this point - if you do this part wrong, everything else will be wrong as well. Next, you need to derive expressions for the scale factors and unit orts e, of the hyperbolic coordinate system: he (3) e. (4) Use the derived expressions to show that the coordinate system you have built is indeed an orthogonal one. Also, show that the system is right-handed, l.e. that the triple of vectors (e, c.cz) (In this order) is a right-handed triple of vectors