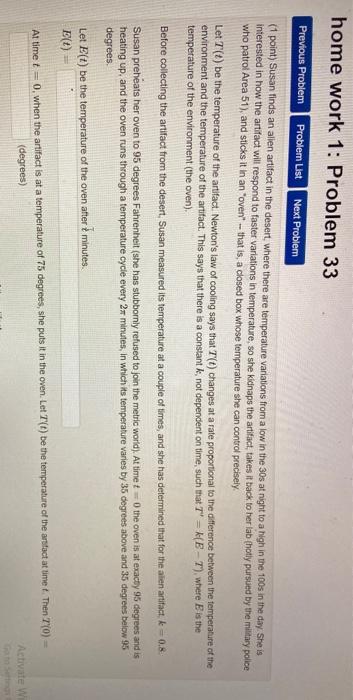
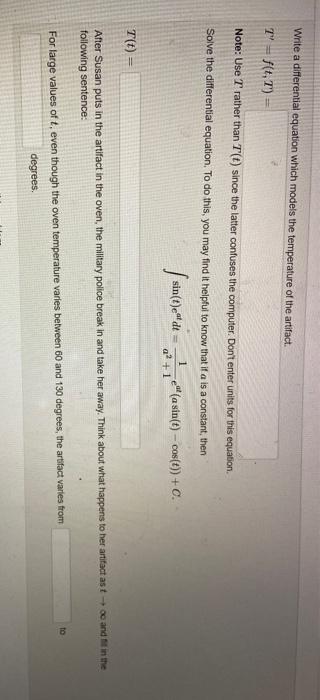
home work 1: Problem 33 Previous Problem Problem List Next Problem (1 point) Susan finds an alien artifact in the desert where there are temperature variations from a low in the 30s at right to a high in the 100s in the day. She is interested in how the artifact will respond to faster variations in temperature, so she kidnaps the artifact, takes it back to her lab (hotly pursued by the military police who patrol Area 51), and sticks it in an "ovent - that is, a closed box whose temperature she can control precisely. Let T() be the temperature of the artifact. Newton's law of cooling says that T() changes at a rate proportional to the difference between the temperature of the environment and the temperature of the artifact. This says that there is a constant k, not dependent on time, such that T" = {(E-) where is the temperature of the environment the oven). Before collecting the artifact from the desert, Susan measured its temperature at a couple of times, and she has determined that for the alien artifact k = 0.8 Susan preheats her oven to 95 degrees Fahrenheit (she has stubbornly refused to join the metric world). At time to the oven is at exactly 95 degrees and is heating up, and the oven runs through a temperature cycle every 2 minutes, in which its temperature varies by 35 degrees above and 35 degrees below 95 degrees Let E() be the temperature of the oven after 2 minutes. Elt) At time t = 0, when the artifact is at a temperature of 75 degrees, she puts it in the oven. Let Tt) be the temperature of the artact at time. Then TO) (degrees) Activate w Write a differential equation which models the temperature of the artifact. T = f(t,T) - Note: Use T rather than T() since the latter confuses the computer. Don't enter units this equation Solve the differential equation. To do this, you may find it helpful to know that if a is a constant, then sin(t)e de 1 a? +1 (a sin(t) - cos(t))+C. T(t) After Susan puts in the artifact in the oven, the military police break in and take her away. Think about what happens to her artifact as to and it in the following sentence: to For large values of t. even though the oven temperature varies between 60 and 130 degrees, the artifact varies from degrees home work 1: Problem 33 Previous Problem Problem List Next Problem (1 point) Susan finds an alien artifact in the desert where there are temperature variations from a low in the 30s at right to a high in the 100s in the day. She is interested in how the artifact will respond to faster variations in temperature, so she kidnaps the artifact, takes it back to her lab (hotly pursued by the military police who patrol Area 51), and sticks it in an "ovent - that is, a closed box whose temperature she can control precisely. Let T() be the temperature of the artifact. Newton's law of cooling says that T() changes at a rate proportional to the difference between the temperature of the environment and the temperature of the artifact. This says that there is a constant k, not dependent on time, such that T" = {(E-) where is the temperature of the environment the oven). Before collecting the artifact from the desert, Susan measured its temperature at a couple of times, and she has determined that for the alien artifact k = 0.8 Susan preheats her oven to 95 degrees Fahrenheit (she has stubbornly refused to join the metric world). At time to the oven is at exactly 95 degrees and is heating up, and the oven runs through a temperature cycle every 2 minutes, in which its temperature varies by 35 degrees above and 35 degrees below 95 degrees Let E() be the temperature of the oven after 2 minutes. Elt) At time t = 0, when the artifact is at a temperature of 75 degrees, she puts it in the oven. Let Tt) be the temperature of the artact at time. Then TO) (degrees) Activate w Write a differential equation which models the temperature of the artifact. T = f(t,T) - Note: Use T rather than T() since the latter confuses the computer. Don't enter units this equation Solve the differential equation. To do this, you may find it helpful to know that if a is a constant, then sin(t)e de 1 a? +1 (a sin(t) - cos(t))+C. T(t) After Susan puts in the artifact in the oven, the military police break in and take her away. Think about what happens to her artifact as to and it in the following sentence: to For large values of t. even though the oven temperature varies between 60 and 130 degrees, the artifact varies from degrees