Homework

In this homework you are going to implement functions necessary for linear regression problem. Consider the following dataset.

*******

Dataset:

import numpy as np import matplotlib.pyplot as plt np.random.seed(42) x = np.linspace(0,3,30) y = 2*x + 3 + np.random.randn(x.size)

plt.plot(x,y,"*") plt.xlabel("x") plt.ylabel("y") plt.grid(True)

*****

Problem 1

def predict_first(x,beta0,beta1): pass

# Problem 1 example

beta0 = 1 beta1 = 2 yhat = predict_first(x,beta0,beta1) print(yhat[5])

2.0344827586206895

Problem 2

In the second problem, you are going to predicted the ^yy^ values again. but this time you are going to use matrix multiplication. Assume you have an input matrix X of shape mk and parameter vector of size k. Use the np.dot() function for matrix multiplication

For the given dataset, you need to add columns of ones to the input vector x so you will have a matrix of shape 302302. You can use np.stack() function to combine vectors or matrices.

X = # write your function here to add columns of ones

# Problem 2.a example print(X[3,:])

[1. 0.31034483]

def predict(X,beta): pass

# Problem 2.b example np.random.seed(42) beta = np.random.random(X.shape[1]) yhat = predict(X,beta) print(yhat[5])

0.8662888980249054

Problem 3

For this problem you are going to implement three performance measures of a regression model, namely, mean squared error (mse), mean absolute error (mae) and mean absolute percentage error (mape).

def mse(y,ypred): pass

def mae(y,ypred): pass

def mape(y,ypred): pass

# Problem 3 example

np.random.seed(42) beta = np.random.random(X.shape[1]) yhat = predict(X,beta)

print("mse :", mse(y,yhat)) print("mae :", mae(y,yhat)) print("mape :", mape(y,yhat))

mse : 17.18425929439018 mae : 4.011241525686726 mape : 70.24040053349047

Problem 4

In problem 4 you are going to calculate the gradients of coefficients at specific points. Assume you have a linear regression model below

y=₀+₁x₁+₂x₂++_kx_k

and the loss function defined as L =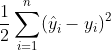

gradients of i can be calculated as follows :

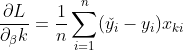
Write a function that will calculate the derivative of parameters. Input parameters of your function should be; input matrix X of shape nk, target variable vector y of size n and the coefficient vector of size k. Your out put should be gradient vector of coefficients 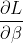of size k

def gradient_beta(X,y,beta): pass

# Problem 4 example np.random.seed(42) beta = np.random.random(X.shape[1])

print("Gradients are :", gradient_beta(X,y,beta))

Gradients are : [-4.01124153 -6.58576749]

Problem 5

Next you are going to update the coefficient using gradients according to following formula:

.

.

.

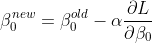
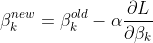
def update_weights(beta, gradient_beta, alpha): pass

# Problem 5 example

np.random.seed(42) beta = np.random.random(X.shape[1]) dbeta = np.random.random(X.shape[1])*3 alpha = 0.1

print("Updated Weights are :", update_weights(beta, dbeta, alpha))

Updated Weights are : [0.15494194 0.77111676]

Problem 6

Now you need to combine all the components together to estimate the coefficients of a linear model. Input parameters of the function will be input matrix X of shape nk and target vector y of size n

def model_fit(X,y,beta, alpha, max_iter): pass

# Problem 6 example

np.random.seed(42) beta_init = np.random.random(X.shape[1]) alpha = 0.1 max_iter = 100 print("Coefficients are:", model_fit(X,y,beta_init, alpha, max_iter))

Coefficients are: [3.07696894 1.78926474]