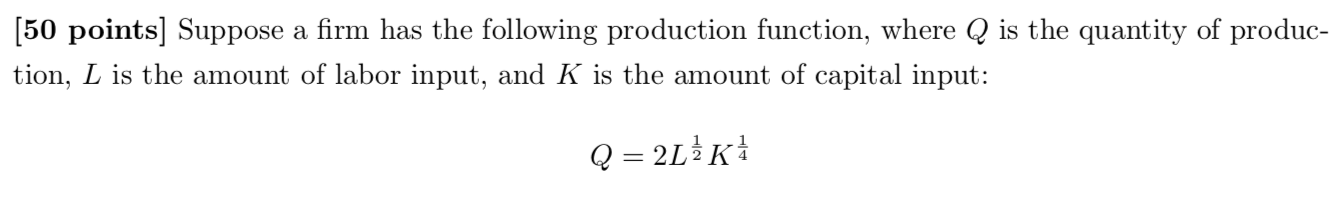How do I answer this?

[50 points] Suppose a firm has the following production function, where Q is the quantity of produc- tion, L is the amount of labor input, and K is the amount of capital input: Q = 2LEK(a) [7 points] Does this production function have increasing, constant, or decreasing returns to scale? How do you know? (b) [7 points] Find the marginal products of labor and of capital, as well as the marginal rate of technical substitution of labor for capital. Suppose now that the rm's capital resource is such that by using more capital, the per-unit cost of capital is reduced. Remember, r is supposed to capture all the costs of capital, and in reality this may include, for instance, maintenance costs as well as rents. Given a certain amount of labor input, additional capital units may mean less wear and tear on each, bulk discounts on rent, and other savings. (c) [7 points] Explain why this idea could be represented by the following total cost function: TC=wL+r\\/E (d) [7 points] As we studied it, the equimarginal principle states that, at an optimal bundle of inputs, it must be that M PL M PK 10 'l" However, in the present case, this would be inaccurate. Explain why the above expression of the equimarginal principle is a special case of a more general form, MPL _ MPK MCI, ' MCK' where M C, is the marginal cost of one productive unit of input 3', and why this more general form can be applied in this new case where costs per productive unit of capital are decreasing. (e) [8 points] Find M CL and M CK from the total cost function in part (c), and use the generalized equimarginal principle to nd the rm's cost-minimizing bundle of L and K when producing any quantity Q (as a function of Q, m, and r). (f) [7 points] Suppose w = 'r. At what levels of production Q will the rm use more capital than labor? Explain why this condition makes sense even though capital is less productive than labor, making reference to the rm's unique total cost function. (g) [7 points] (Stop assuming 11: = 'r.) Using your expression for the cost-minimizing bundle, rewrite the total cost function and simplify to Show that TC = QM. Suppose this rm is a represen- tative rm in a perfectly competitive industry (that is, every other rm is just like this one). In the long run, given this cost function, what will be the equilibrium price in this market? (Your answer will be in terms of w and r.)