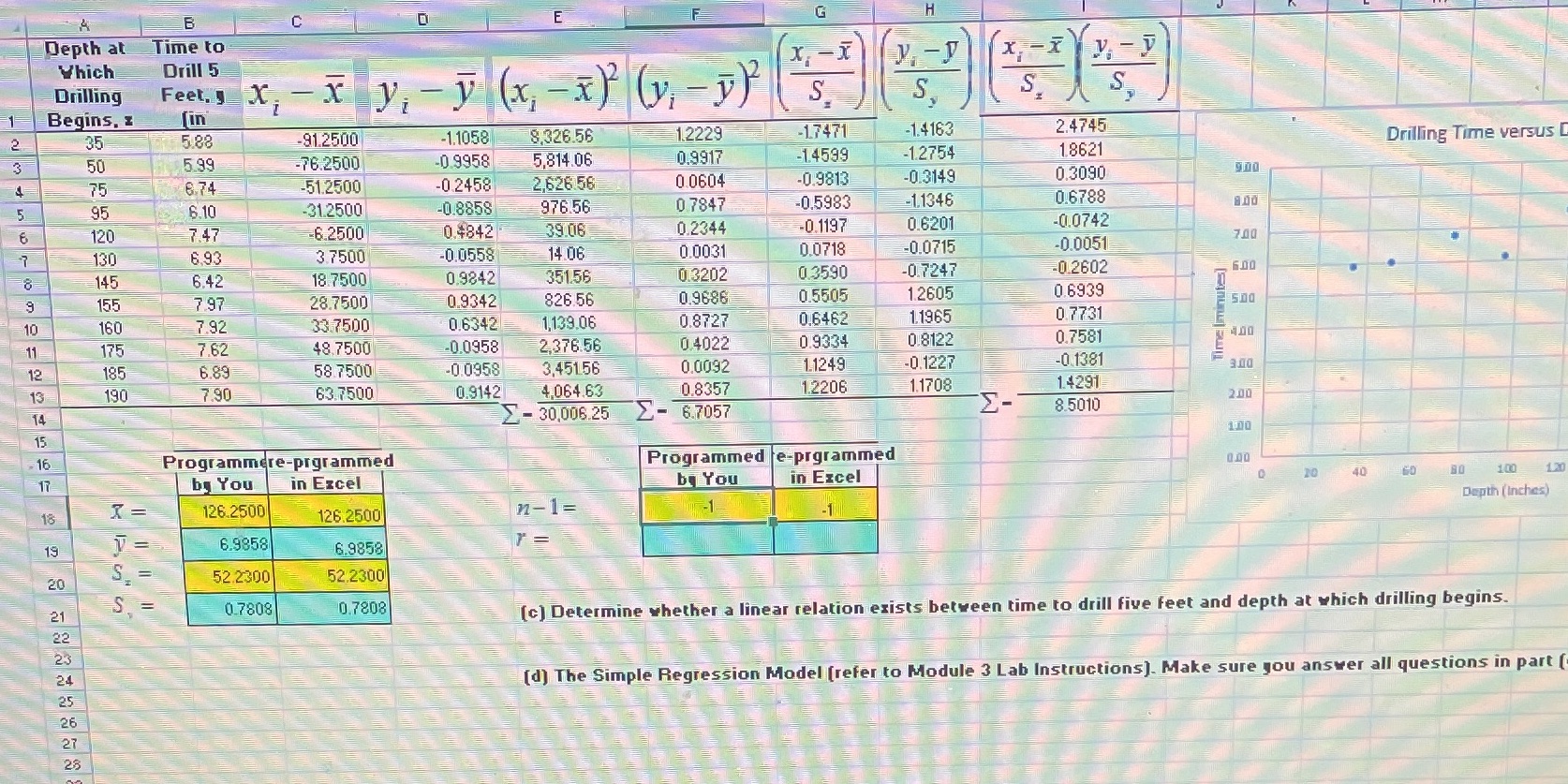
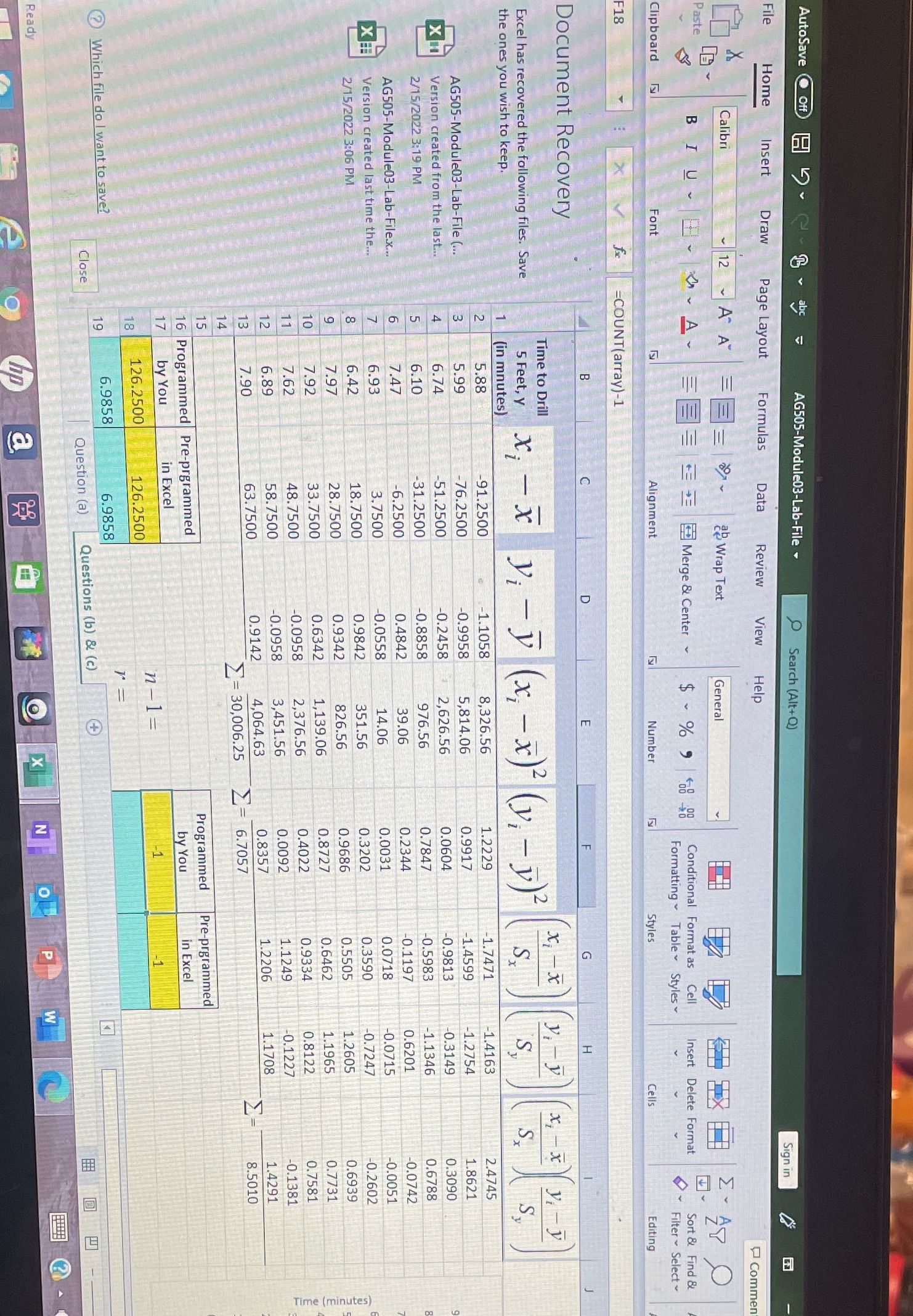
How do I calculate r and is the n-1 correct the boxes that are yellow and teal

B C E F G H Depth at Time to Which Drill 5 X, -X X - X Drilling Begins. z x , - x y, V ( x, - x ) (V, J ) S. S. S [in 35 5.28 91.2500 -1.1058 8,326.56 1.2229 -1.7471 -1.4163 2.4745 50 5.99 -76.2500 0.9958 5,814.06 0.9917 -1.4599 -1.2754 1.8621 Drilling Time versus 75 6.74 -51.2500 -0.2458 2,626 56 0.0604 -0.9813 -0.3149 0.3090 95 6.10 31.2500 0.8858 976.56 0 7847 0.5983 -1.1346 0.6788 6 120 7.47 -6.2500 0.4842 39.06 0.2344 -0.1197 0.6201 -0.0742 130 6.93 3.7500 0.0558 14 06 0.0031 0.0718 -0.0715 -0.0051 8 145 6.42 18.7500 0.9842 351.56 013202 0.3590 -0.7247 -0.2602 9 155 7.97 28.7500 0.9342 826.56 0.9686 0.5505 1.2605 0.6939 10 160 7.92 33.7500 0.6342 1,139.06 510 0.8727 0.6462 1.1965 0.7731 11 175 7.62 48.7500 0.0958 2,376.56 0.4022 0.9334 0.8122 0.7581 12 185 6.89 58.7500 0.0958 3,45156 0.0092 1.1249 -0.1227 -0 1381 13 190 7.90 63.7500 0.9142 4,064.63 0.8357 1.2206 1.1708 1.4291 14 2- 30,006.25 E- 6.7057 E- 8.5010 2.10 15 -16 Programmere-prgrammed Programmed e-prgrammed 17 by You in Excel b You in Excel 40 1.00 1X X = 126.2500 126.2500 n-1= Depth (Inches) 19 V= 6.9858 6.9853 20 52.2300 52.2300 21 0.7808 0.7808 22 (c) Determine whether a linear relation exists between time to drill five feet and depth at which drilling begins. 23 24 25 (d) The Simple Regression Model [refer to Module 3 Lab Instructions). Make sure you answer all questions in part ( 26 27 23AutoSave O Off & abc AG505-Module03-Lab-File - Search (Alt+Q) File Sign in Home Insert Draw Page Layout Formulas Data Review View Help Commen Calibri 12 ~ A A E E ab Wrap Text General aste E - AY O E Merge & Center Conditional Format as Cell Insert Delete Format Sort & Find & Formatting ~ Table Styles ~ Filter ~ Select ~ Clipboard LA Font Alignment 12 Number Styles Cells Editing 18 =COUNT(array)-1 U LL WU Document Recovery Time to Drill x VI - y Excel has recovered the following files. Save 5 Feet, y the ones you wish to keep. Vi - y x, - x ( V, - V) (in mnutes) 5.88 -91.2500 -1.1058 8,326.56 1.2229 -1.7471 -1.4163 2.4745 AG505-Module03-Lab-File (.. 5.99 76.2500 0.9958 5,814.06 0.9917 1.4599 1.2754 1.8621 KH Version created from the last. 6.74 -51.2500 -0.2458 2,626.56 0.0604 -0.9813 0.3149 0.3090 2/15/2022 3:19 PM 6.10 31.2500 0.8858 976.56 0.7847 0.5983 1.1346 0.6788 AG505-Module03-Lab-File.x. 7.47 6.2500 0.4842 39.06 0.2344 0.1197 0.6201 0.0742 0.0051 Version created last time the.. 6.93 3.7500 0.0558 14.06 0.0031 0.0718 -0.0715 2/15/2022 3:06 PM 6.42 18.7500 0.9842 351.56 0.3202 0.3590 0.7247 0.2602 28.7500 0.9342 826.56 0.5505 1.2605 0.6939 7.97 0.9686 0.7731 Time (minutes) 7.92 33.7500 0.6342 1,139.06 0.8727 0.6462 1.1965 0.7581 7.62 48.7500 0.0958 2,376.56 0.4022 0.9334 0.8122 0.0092 1.1249 0.1381 N 6.89 58.7500 0.0958 3,451.56 -0.1227 0.8357 1.2206 1.1708 1.4291 7.90 63.7500 0.9142 4,064.63 W = 30,006.25 = 6.7057 8.5010 Programmed Pre-prgrammed 16 Programmed Pre-prgrammed by You in Excel by You in Excel 126.2500 126.2500 n-1= H CO 2 Which file do I want to save? 6.9858 6.9858 + Close Question (a) Questions (b) & (c) E 3 Ready 2URE RICH. ET FRIENDLY. 7 29% 13-39 Wed Feb 16 Today li Edit V 13:39 HP Connected Apps' W This sum gives you this value Et=1 xi - a yi - y Sy r= Programing the Formulas 18.In cell F19, you will compute the value of the correlation coefficient by programing the formula yourself. Use the sum obtained from cells 114 and value of (n-1) in cell F18. 19. Verify the value of the correlation coefficient obtained in cell F19 by using the Excel pre- programmed formula for sample correlation coefficient in cell G19. That is, use the formula =correl(array1,array2) where array1 is the range of values for variable x and array2 is the range of values for variable y