How do i solve 7

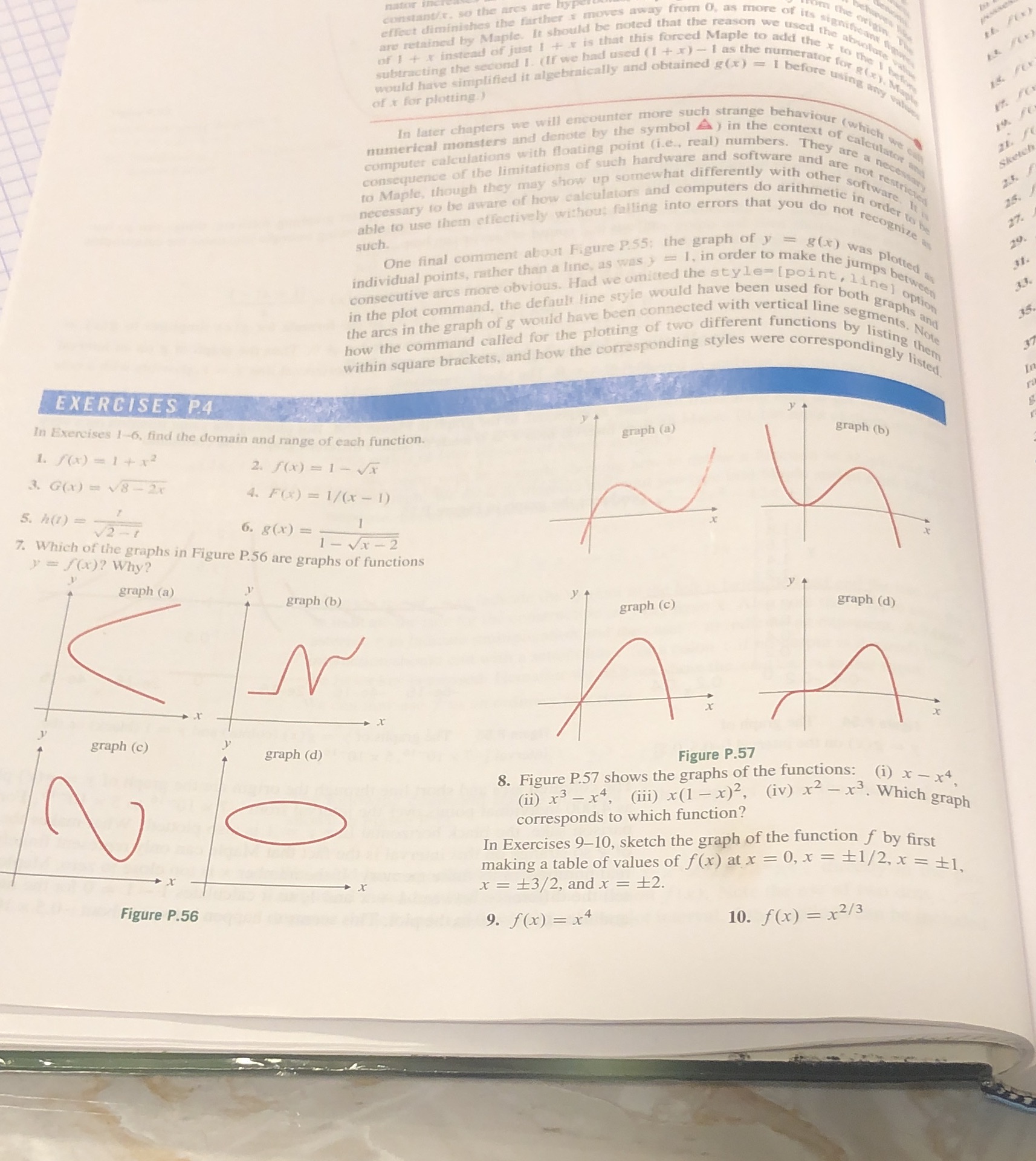
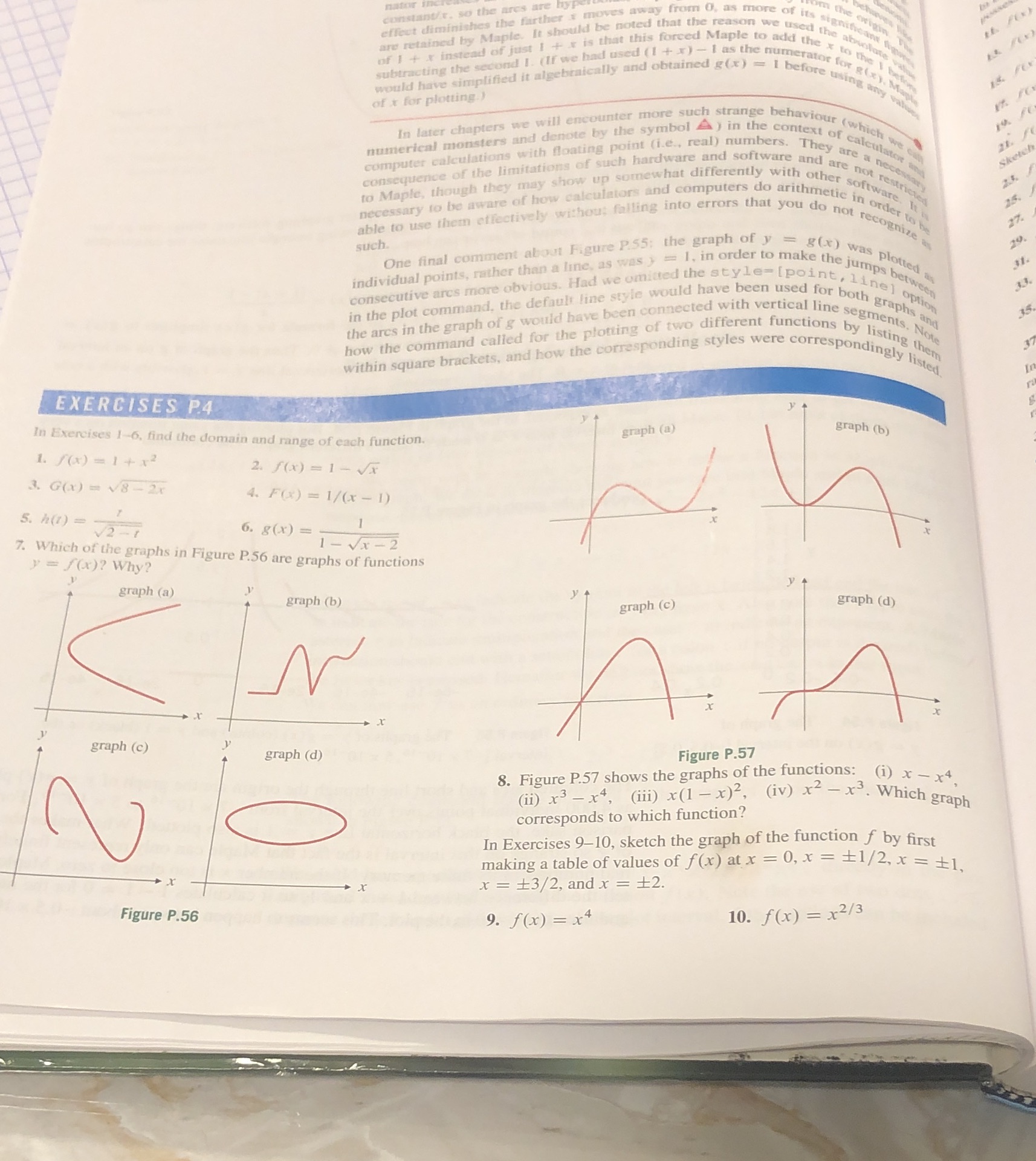
constant/c. so the ares are effect diminishes the further a moves away from 0. as more retained by Maple. It should be noted that the reason we med the about of 1 + + instead of just 1 + x is that this forced Maple to and the x to pole subtracting the sec pond I. (If we had used (1 + x) - I as the numerator for gently have simplified it algebraically and obtained see) - before using any way of x for plotting.) In later chapters we will encounter more such strange beniasfour (which numerical monsters and denote by the symbol A ) in the content of calculate computer calculations with floating point (i.e., real) numbers. They are a necess consequence of the limitations of such hardware and software and are not rella sketch to Maple, though they may show up somewhat differently with other softygatri necessary to be aware of how calculators and computers do timeinone in order it is able to use them effectively without falling into errors that you do not recogn he such. One final comment about Figure P.$5; the graph of y y = g(x) was plotted as individual points, rather than a line, as was } = 1, in order to make the jumps ber as Consecutive arcs more obvious. Had we omitted the style theft, line] open in the plot command. the default line style would have been used for both graphs of the ares in the graph of g would have been connected with verncutline segments, yl now the command called for the plotting of two different functions by listing thite Within square brackets, and how the corresponding styles were coffespondingly jiseth EXERCISES P.4 In Exercises 1-6, find the domain and range of each function. graph (b) 1. f ( x) = 1+x2 2. f (x ) = 1- Vx 3. G(x) = V8-2 4. F() = 1/(x -1) 5. h(1) =- V2 - 1 6. 8 (x) = - 1 - Vx - 2 7. Which of the graphs in Figure P.56 are graphs of functions y = f(x)? Why? graph (a) graph (b) graph (c) graph (d) graph (c) graph (d) Figure P.57 8. Figure P.57 shows the graphs of the functions: (i) x - x4 (ii) x3 - x4, (iii) x (1 -x)2, (iv) x2 - x3. Which graph corresponds to which function? In Exercises 9-10, sketch the graph of the function f by first making a table of values of f(x) at x = 0, x = #1/2, x = +1, x = 13/2, and x = #2. Figure P.56 9. f ( x ) = x4 10. f (x) = x2/3