How to gate table 1 using matlab code , write the all code and run the code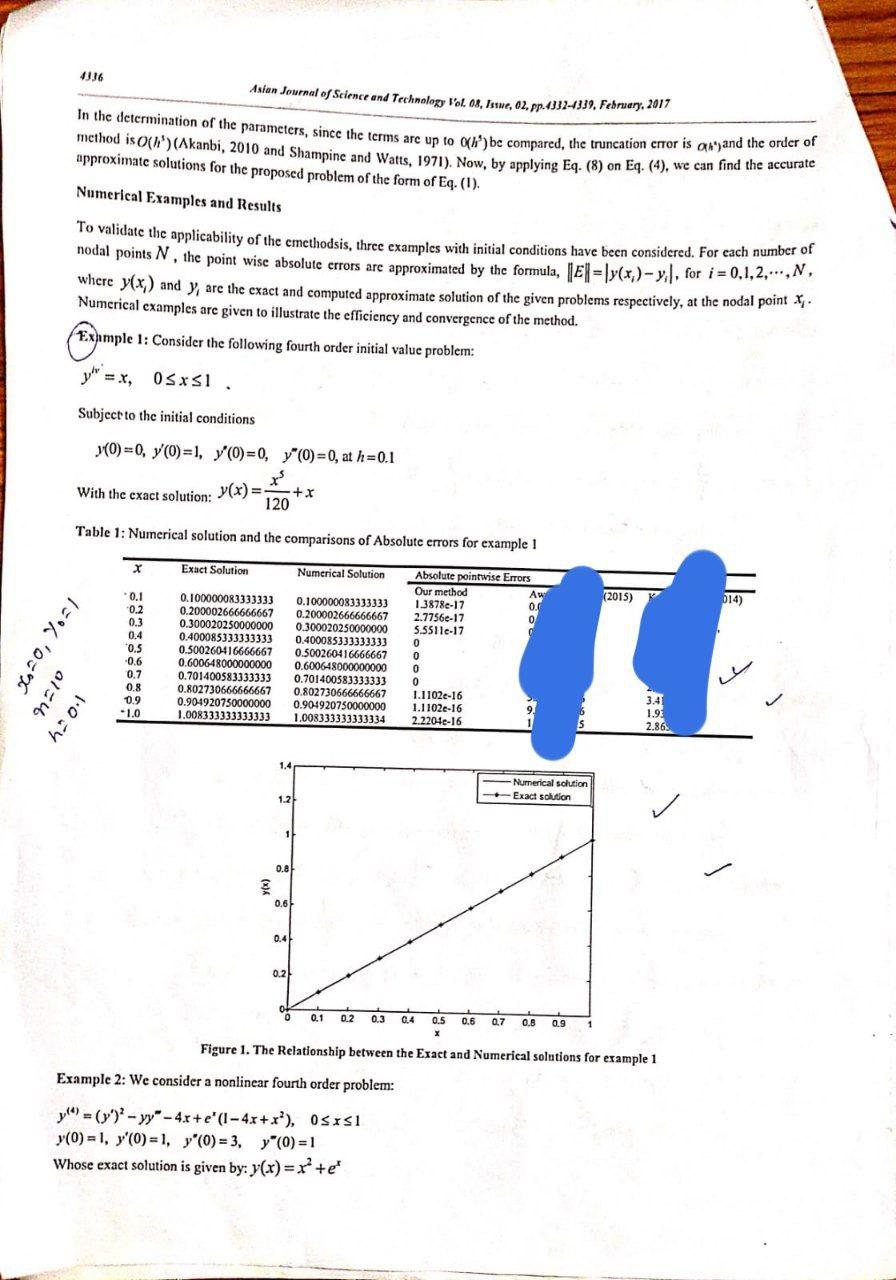

4336 01=46 Asian Journal of Science and Technology Vol. 08, Issue, 02, pp. 4332-4339, February, 2017 In the determination of the parameters, since the terms are up to 0(h) be compared, the truncation error is and the order of method is 0(h) (Akanbi, 2010 and Shampine and Watts, 1971). Now, by applying Eq. (8) on Eq. (4), we can find the accurate approximate solutions for the proposed problem of the form of Eq. (1). Numerical Examples and Results To validate the applicability of the emethodsis, three examples with initial conditions have been considered. For each number of nodal points N, the point wise absolute errors are approximated by the formula, E-ly(x)-y, for i=0.1,2,.., N. where y(x) and y, are the exact and computed approximate solution of the given problems respectively, at the nodal point X. Numerical examples are given to illustrate the efficiency and convergence of the method. Example 1: Consider the following fourth order initial value problem: y=x, 0xl. Subject to the initial conditions (0) 0, y(0)=1, y(0)= 0, y(0)=0, at h=0.1 With the exact solution: y(x)= 1=0/10=50 120 Table 1: Numerical solution and the comparisons of Absolute errors for example 1 Numerical Solution Absolute pointwise Errors Our method 1.3878e-17 0.200002666666667 2.7756e-17 0.100000083333333 1.0=4 x 0.1 0.2 0.3 0.4 0.5 -0.6 0.7 0.8 10.9 -1.0 Exact Solution 0.100000083333333 0.200002666666667 0.300020250000000 0.300020250000000 5.55116-17 0.400085333333333 0.400085333333333 0 0.500260416666667 0.500260416666667 0 0.600648000000000 0.600648000000000 0 0.701400583333333 0.701400583333333 0 0.802730666666667 0.802730666666667 0.904920750000000 0.904920750000000 1.1102e-16 1.008333333333333 1.008333333333334 2.2204-16 1.1102e-16 1.4 1.2 1 0.8 0.6 0.4 +x 0.2 0 0.1 0.2 0.3 0,4 Example 2: We consider a nonlinear fourth order problem: y)= (y)-yy"-4x+e' (1-4x+x), 0x1 y(0)= 1, y'(0) = 1, y'(0)=3, y"(0)=1 Whose exact solution is given by: y(x)=x + e* Aw 0.0 0 C 6 5 -Numerical solution Exact solution 0.5 0.6 X Figure 1. The Relationship between the Exact and Numerical solutions for example 1 0,7 (2015) 0.8 0.9 1 3.41 1.93 2.86 014)