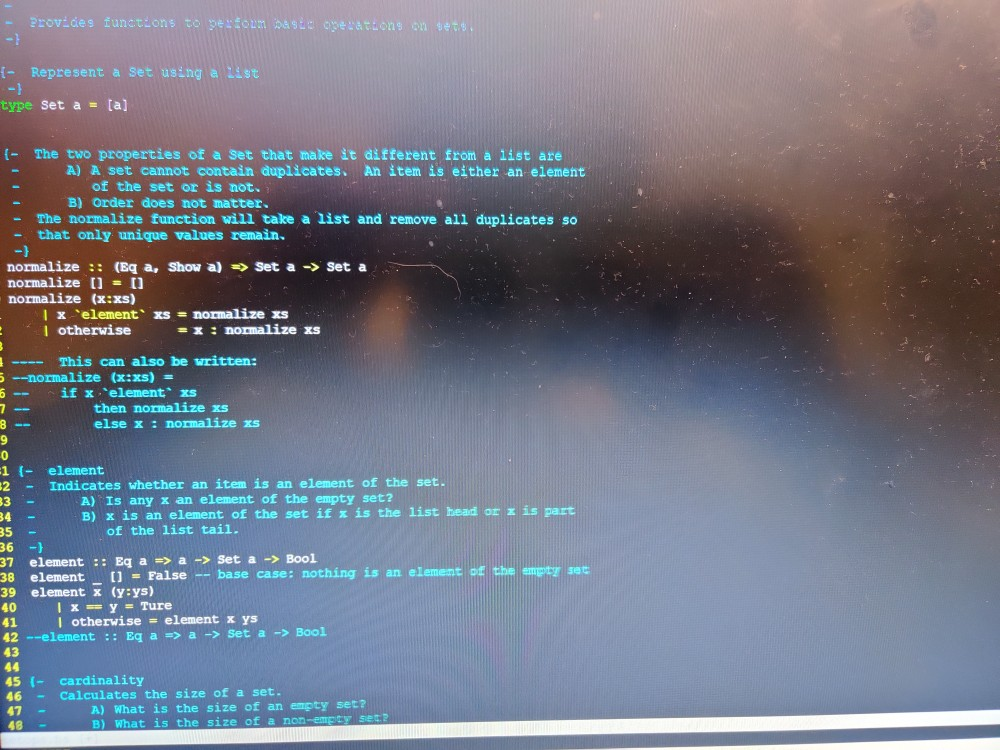
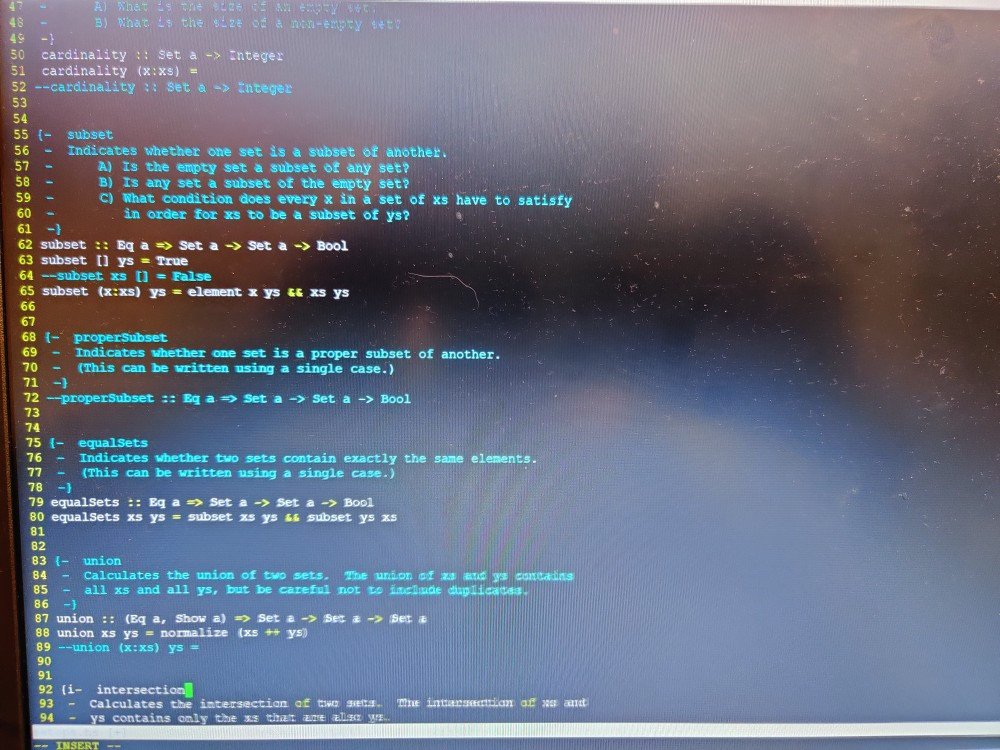
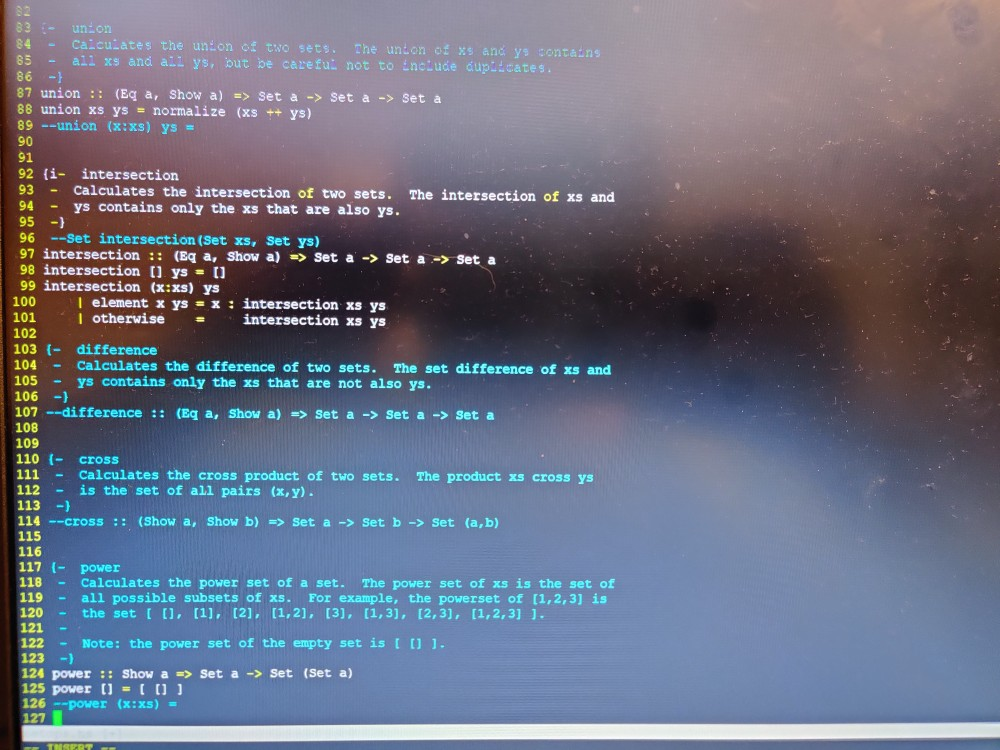
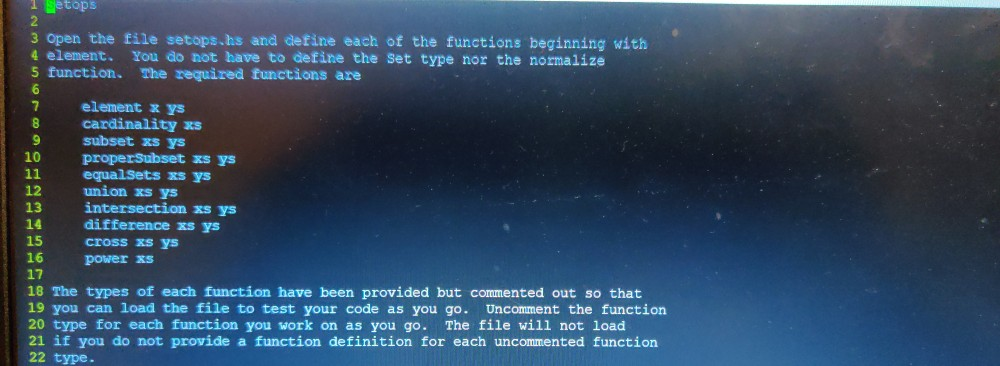
How to write code for these functions in haskell. Some of them are completed some are not completed.

Provides functions to be com waste operations on gets. {- Represent a set using a list type Set a = (a) (- The two properties of a set that make it different from a list are A) A set cannot contain duplicates. An item is either an element of the set or is not. B) Order does not matter. The normalize function will take a list and remove all duplicates so that only unique values remain. - normalize :: (Eq a, Show a) => Set a -> Set a normalize [] = [] normalize (x:xs) | x-'elements = normalize xs | otherwise =x: normalize xs This can also be written: --normalize (x:xs) = -- if x 'elements then normalize xs else x : normalize xs 19 . {- IIIII element Indicates whether an item is an element of the set. A) Is any x an element of the empty set? B) x is an element of the set if x is the list head or x is part of the list tail. element :: Eg a => a -> Set a -> Bool 38 element [] = False -- base case: nothing is an element of the empty set element X (y:ys) x == Y = Ture I otherwise - element x ys 42 --element :: Eg a => a -> Set a -> Bool 39 41 45 (- 46 - cardinality Calculates the size of a set. A) What is the size of an empty set? B) What is the size of a non-empty 48 - A) What the e B) What s the $20 a non-empty to 50 cardinality :: Set -> Integer 51 cardinality (x:xs) = 52 --cardinality :: Set & -> Integer 55 - - Tim subset Indicates whether one set is a subset of another, A) Is the empty set a subset of any set? B) Is any set a subset of the empty set? c) What condition does every x in a set of Xs have to satisfy in order for xs to be a subset of ys? 62 subset :: Eq a => set a -> Set a -> Bool 63 subset 1) ys = True 64 --subset xs 0 = False 65 subset (x:xs) ys = element x ys et xs ys 68 - properSubset 69 - Indicates whether one set is a proper subset of another. 70 - (This can be written using a single case.) 71 -) 72 --properSubset :: Eg a => Set a -> Set a -> Bool 73 74 75 - equalsets 76 - Indicates whether two sets contain exactly the same elements. 77 - (This can be written using a single case.) 78 -) 79 equalSets :: Eg a => Set a -> Set a -> Bool 80 equalSets xs ys = subset xs ys & subset ys as 82 83 - union 84 - Calculates the union of two sets. The DOT CE 23 y contains 85 - all xs and all ys, but be careful not to cade duplicates 86 -) 87 union :(Eq a, Show a) >> Set 2 -> Ses 2 -> Set 88 union xs ys = normalize (x + ys) 89 --union (x:xs) ys = 92 (i- intersection 93 - Calculates the intersection of the 94 - y contains only the E E o at an came int ESE TONSERT 83 - union 84 - Calculates the union o two sets. The union of XS and ys contains 85 - all xs and ail ys, but be carefu: not to include dupiicates. 86 } 87 union :: (Eq a, Show a) => Set a -> Set a -> Set a 88 union xs ys = normalize (xs ++ ys) 89 --union (x:xs) ys = 90 92 (i- intersection 93 - Calculates the intersection of two sets. The intersection of xs and ys contains only the xs that are also ys. 95 -1 96 --Set intersection (Set xs, set ys) 97 intersection :: (Eg a, Show a) > Set a -> Set a-> 98 intersection () ys = [] 99 intersection (x:xs) ys 100 1 element x y = x : intersection xs ys 101 I otherwise = intersection xs ys 103 - difference 104 - Calculates the difference of two sets. The set difference of xs and 105 Ys contains only the xs that are not also ys. 106 107 --difference :: (Eq a, show a) => Set a -> Set a -> Set a 108 110 (- cross 111 - Calculates the cross product of two sets. The product xs cross ys is the set of all pairs (x,y). --cross :: (Show a, show b) => Set a -> Set b -> Set (a,b), 116 117 (- power Calculates the power set of a set. The power set of xs is the set of - all possible subsets of xs. For example, the powerset of (1,2,3) 15 120 - the set ( 0), (1), (2), (1,2), (3), (1,3), (2,3), (1,2,3] ). - Note: the power set of the empty set is 10). 124 power :: Show a => Set a -> Set (Set a) 125 power () = ( 11 ) 126 --power (x:xs) = 127 1 Setops 3 Open the file setops.hs and define each of the functions beginning with 4 element. You do not have to define the set type nor the normalize 5 function. The required functions are BURBEVO element x ys cardinality as subset xs ys properSubset xs ys equalSets xs ys union xs ys intersection xs ys difference xs ys cross xs ys power xs 18 The types of each function have been provided but commented out so that 19 you can load the file to test your code as you go. Uncomment the function 20 type for each function you work on as you go. The file will not load 21 if you do not provide a function definition for each uncommented function 22 type. Provides functions to be com waste operations on gets. {- Represent a set using a list type Set a = (a) (- The two properties of a set that make it different from a list are A) A set cannot contain duplicates. An item is either an element of the set or is not. B) Order does not matter. The normalize function will take a list and remove all duplicates so that only unique values remain. - normalize :: (Eq a, Show a) => Set a -> Set a normalize [] = [] normalize (x:xs) | x-'elements = normalize xs | otherwise =x: normalize xs This can also be written: --normalize (x:xs) = -- if x 'elements then normalize xs else x : normalize xs 19 . {- IIIII element Indicates whether an item is an element of the set. A) Is any x an element of the empty set? B) x is an element of the set if x is the list head or x is part of the list tail. element :: Eg a => a -> Set a -> Bool 38 element [] = False -- base case: nothing is an element of the empty set element X (y:ys) x == Y = Ture I otherwise - element x ys 42 --element :: Eg a => a -> Set a -> Bool 39 41 45 (- 46 - cardinality Calculates the size of a set. A) What is the size of an empty set? B) What is the size of a non-empty 48 - A) What the e B) What s the $20 a non-empty to 50 cardinality :: Set -> Integer 51 cardinality (x:xs) = 52 --cardinality :: Set & -> Integer 55 - - Tim subset Indicates whether one set is a subset of another, A) Is the empty set a subset of any set? B) Is any set a subset of the empty set? c) What condition does every x in a set of Xs have to satisfy in order for xs to be a subset of ys? 62 subset :: Eq a => set a -> Set a -> Bool 63 subset 1) ys = True 64 --subset xs 0 = False 65 subset (x:xs) ys = element x ys et xs ys 68 - properSubset 69 - Indicates whether one set is a proper subset of another. 70 - (This can be written using a single case.) 71 -) 72 --properSubset :: Eg a => Set a -> Set a -> Bool 73 74 75 - equalsets 76 - Indicates whether two sets contain exactly the same elements. 77 - (This can be written using a single case.) 78 -) 79 equalSets :: Eg a => Set a -> Set a -> Bool 80 equalSets xs ys = subset xs ys & subset ys as 82 83 - union 84 - Calculates the union of two sets. The DOT CE 23 y contains 85 - all xs and all ys, but be careful not to cade duplicates 86 -) 87 union :(Eq a, Show a) >> Set 2 -> Ses 2 -> Set 88 union xs ys = normalize (x + ys) 89 --union (x:xs) ys = 92 (i- intersection 93 - Calculates the intersection of the 94 - y contains only the E E o at an came int ESE TONSERT 83 - union 84 - Calculates the union o two sets. The union of XS and ys contains 85 - all xs and ail ys, but be carefu: not to include dupiicates. 86 } 87 union :: (Eq a, Show a) => Set a -> Set a -> Set a 88 union xs ys = normalize (xs ++ ys) 89 --union (x:xs) ys = 90 92 (i- intersection 93 - Calculates the intersection of two sets. The intersection of xs and ys contains only the xs that are also ys. 95 -1 96 --Set intersection (Set xs, set ys) 97 intersection :: (Eg a, Show a) > Set a -> Set a-> 98 intersection () ys = [] 99 intersection (x:xs) ys 100 1 element x y = x : intersection xs ys 101 I otherwise = intersection xs ys 103 - difference 104 - Calculates the difference of two sets. The set difference of xs and 105 Ys contains only the xs that are not also ys. 106 107 --difference :: (Eq a, show a) => Set a -> Set a -> Set a 108 110 (- cross 111 - Calculates the cross product of two sets. The product xs cross ys is the set of all pairs (x,y). --cross :: (Show a, show b) => Set a -> Set b -> Set (a,b), 116 117 (- power Calculates the power set of a set. The power set of xs is the set of - all possible subsets of xs. For example, the powerset of (1,2,3) 15 120 - the set ( 0), (1), (2), (1,2), (3), (1,3), (2,3), (1,2,3] ). - Note: the power set of the empty set is 10). 124 power :: Show a => Set a -> Set (Set a) 125 power () = ( 11 ) 126 --power (x:xs) = 127 1 Setops 3 Open the file setops.hs and define each of the functions beginning with 4 element. You do not have to define the set type nor the normalize 5 function. The required functions are BURBEVO element x ys cardinality as subset xs ys properSubset xs ys equalSets xs ys union xs ys intersection xs ys difference xs ys cross xs ys power xs 18 The types of each function have been provided but commented out so that 19 you can load the file to test your code as you go. Uncomment the function 20 type for each function you work on as you go. The file will not load 21 if you do not provide a function definition for each uncommented function 22 type