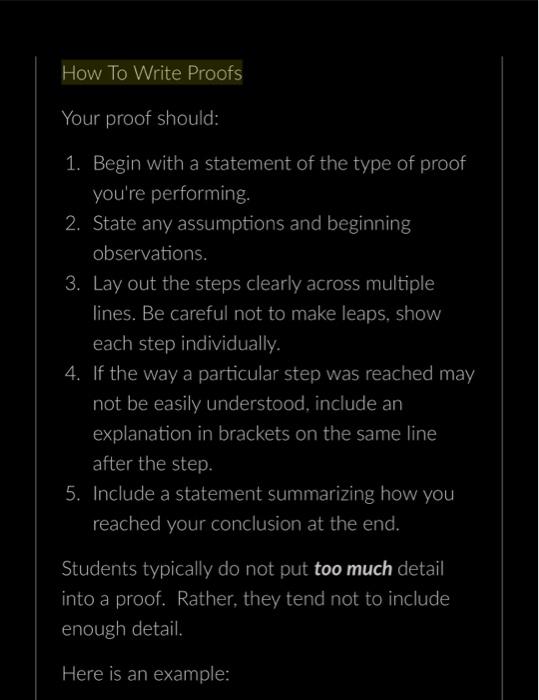
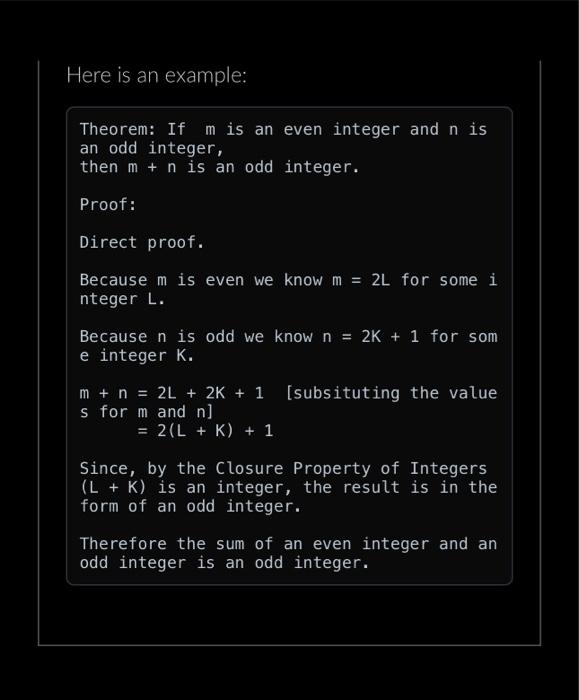
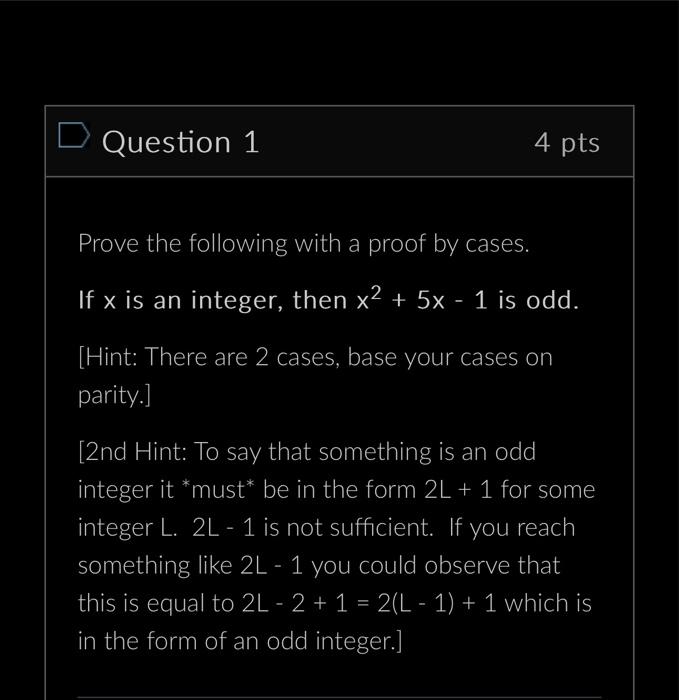
How To Write Proofs Your proof should: 1. Begin with a statement of the type of proof you're performing. 2. State any assumptions and beginning observations. 3. Lay out the steps clearly across multiple lines. Be careful not to make leaps, show each step individually. 4. If the way a particular step was reached may not be easily understood, include an explanation in brackets on the same line after the step. 5. Include a statement summarizing how you reached your conclusion at the end. Students typically do not put too much detail into a proof. Rather, they tend not to include enough detail. Here is an example: Here is an example: Theorem: If m is an even integer and n is an odd integer, then m + n is an odd integer. Proof: Direct proof. Because m is even we know m = 2L for some i nteger L. Because n is odd we know n = 2K + 1 for som e integer K. m + n = 2L + 2K + 1 [subsituting the value s for m and n] = 2(L + K) + 1 Since, by the Closure Property of Integers (L + K) is an integer, the result is in the form of an odd integer. Therefore the sum of an even integer and an odd integer is an odd integer. D Question 1 4 pts Prove the following with a proof by cases. If x is an integer, then x + 5x - 1 is odd. [Hint: There are 2 cases, base your cases on parity.] [2nd Hint: To say that something is an odd integer it *must be in the form 2L+ 1 for some integer L. 2L - 1 is not sufficient. If you reach something like 2L - 1 you could observe that this is equal to 2L - 2 + 1 = 2(L-1) + 1 which is in the form of an odd integer.] D Question 2 4 pts Prove the following with a proof by cases. If integers x and y have the same parity, then x + y is even. (Hint: There are 2 cases, one of the cases is where both x and y are even.) D Question 3 4 pts Prove the following with a proof by cases. If x and y are real numbers, then max(x, y) + min(x, y) = x + y. Where max(x, y) is the greater between x and y and min(x, y) is the lesser between x and y.