How were the calculations done? need help writing a lab report pls and thanks.

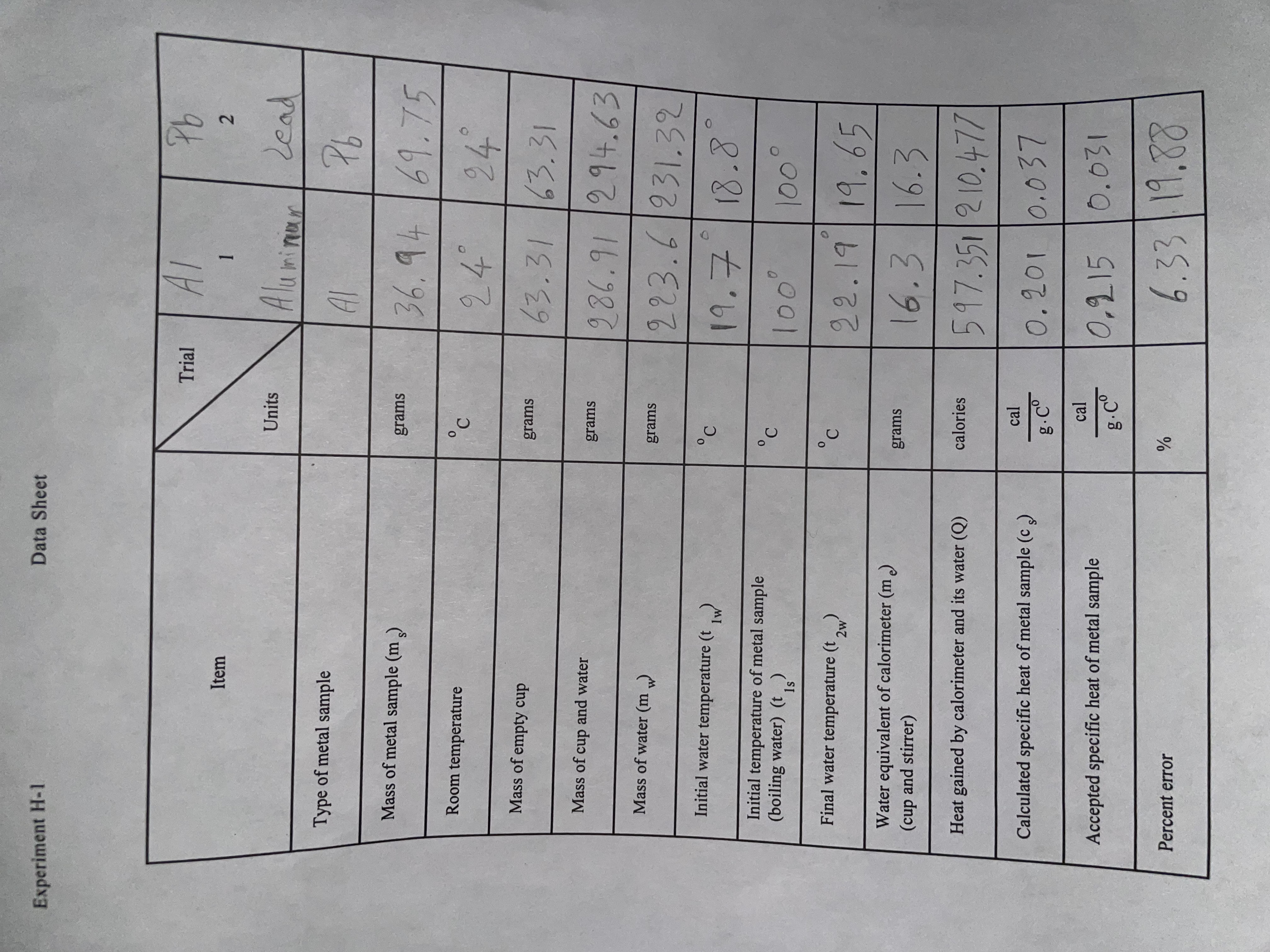
Experiment H-1 Data Sheet Trial Al Pb Item - 2 Units Aluminium lead Type of metal sample Al Pb Mass of metal sample (ms) grams 36. 94 / 69. 75 Room temperature 24 24 Mass of empty cup grams 63 . 31 163 . 31 Mass of cup and water grams 986. 91 / 294. 63 Mass of water (m grams 223. 6 / 231. 32 Initial water temperature (t C 19 . 7 18.8 Initial temperature of metal sample C (boiling water) (t) 100 100 Final water temperature (t,) C 22. 19 19. 65 Water equivalent of calorimeter (m ) grams (cup and stirrer 16.3 16.3 Heat gained by calorimeter and its water (Q) calories 597. 351 210. 471 cal Calculated specific heat of metal sample (c ) g . Co 0. 201 10. 037 cal Accepted specific heat of metal sample 0, 215 10.031 g . Co Percent error /o 6. 33 19.88SPECIFIC HEAT Purpose The purpose of this experiment is twofold: First to familiarize the student with the theory and practice of heat measurement; and second, to determine the specific heat of a solid. Theory Heat is energy that is being transferred between two bodies, solely due to their difference in temperature. For instance, heat flows from the sun to the earth because the sun is hotter than the earth. This type of heat flow consists of electromagnetic waves flowing through empty space and is known as radiation. When one stirs a hot liquid with a spoon, heat travels from the liquid through the spoon to one's hand, because the liquid is at a higher temperature than the hand. This type of heat transfer through matter but without a transfer of matter is known as conduction. Heat may also flow from a hot body to a colder body due to the flow of a gas or a liquid in a process known as convection. Energy that is flowing from a radio transmitting antenna to a radio receiving antenna could not properly be called heat energy, because the energy flow is not caused by a difference in temperature between the antennas. The addition of heat to a body may have a variety of effects -- as for example those that occur when food is cooked, or water is boiled, or a thermocouple generates electrical energy. But often, the only major effect of adding heat to a body is to increase its temperature. In this case, the heat added Q is related to the increase in temperature At and the mass m of the body by the following equation: Q - mc At (1) c is a constant of proportionality known as the specific heat. Values of the specific heat for various substances are listed in a number of handbooks of physics and chemistry. Since heat is a form of energy, it may be measured in terms of such ordinary units of energy as the erg and the joule. However, heat is often measured in units defined in terms of the ability of heat to cause an increase in temperature. One calorie is the amount of heat that must be added to one gram of water to raise its temperature by one Celsius degree. One BTU (British thermal unit) is the amount of heat that must be added to one pound of water to raise its temperature by one Fahrenheit degree. It follows from these definitions and from equation (1) that the specific heat of water is 1 cal/(g-Co) or BTU/(1b-Fo). In this experiment we shall express all quantities of heat in calories, all masses in grams, all temperatures in degrees Celsius, and all specific heats in call(g.Co). The science of heat measurement is known as calorimetry. One of the more common procedures in calorimetry is known as the "method of mixtures." Basically, this procedure utilizes the principle of heat exchange. When a heat exchange takes place between two bodies initially at different temperatures, the quantity of heat lost by the warmer body is equal to that gained by the colder body, and some intermediate temperature is finally reached. This is true provided no heat is exchanged with the surroundings.To prevent loss of heat to the surroundings, a device known as a calorimeter is employed. Although there are several types of calorimeters, the type to be used in this experiment is the water calorimeter. In its simplest form the water calorimeter consists of a thin-walled metal can. The can contains a measured quantity of water. This can is placed within a second can to provide a heat-insulating air space. A cover of insulating material is used to further reduce heat loss. See Figure 1. If an unknown quantity of heat Q is Figure I Introduced into the calorimeter, Q may be found from the measured rise in the Water Calorimeter temperature of the water in the calorimeter. (Side Cross-sectional View) Q - (m. + m.) cw (12w -[[w) (2) Resistance where: Thermometer Stirrer "mass of water in the calorimeter Rubber Stopper the "water equivalent" of the calorimeter the specific heat of water Inner cal/(g-Co) Cup Fiber Ring 12w the final water temperature Water Metal Outer the initial water temperature Sample Container e water equivalent m, of the calorimeter is the mass of water which would absorb the same amount of heat per degree of temperature increase as the calorimeter cup and stirrers The water equivalent of the calorimeter to be used in this experiment will be provided by the laboratory instructor. In this experiment the unknown quantity of heat Q is added to the calorimeter by placing a heated piece of metal in the calorimeter water. It follows from the law of conservation of energy that the heat lost by the metal sample is just equal to the heat Q gained by the calorimeter. The specific heat of the metal sample c. can easily be calculated, using this value of Q, the mass of the metal sample m,, and the initial temperature of the metal sample t.. It is assumed that the final temperature of the metal sample is the same as the final water temperature t2,. Equation (3) is obtained by using these symbols in equation (1) and solving for c. (3) my (ta - 12w Despite the care taken in the design of the calorimeter, small amounts of heat may still be exchanged between the calorimeter and its environment, contributing a small error in the determination of c,. This source of error can be further minimized by a proper choice of the initial water temperature (w. The initial water temperature to should be as much below the room temperature as the final water temperature is above the room temperature. Under these conditions the heat flowing from the room to the calorimeter during part of the measurement cancels the effect of heat flowing from the calorimeter to the room during the remainder of the measurement. Of course, it is not possible to make a perfect choice of the initial watertemperature, because the temperature rise (12, - 1,,) is not known at the beginning of the experiment. Fortunately, a rough estimate is sufficient for obtaining the required accuracy.A resistance-thermometer probe will be used with a digital multimeter for measuring the temperature of the water in the calorimeter and for measuring room temperature. The probe is inserted into the calorimeter as shown in Figure 1. The test leads from the probe are connected to the common and k$2 jacks on the digital multimeter, and the multimeter is set to its 200 kf) resistance range. Higher temperatures reduce the resistance of the semiconductor in the tip of the probe. A chart will be provided in the laboratory which lists the temperature corresponding to each resistance reading for a range of temperatures near room temperature. (Other laboratories often use resistance thermometers with their own digital readout in .C.) The chart provides a reading to the nearest .01 to .03 .C. Admittedly, the absolute accuracy of the resistance thermometer would not justify readings in such fine steps. But when we are trying to measure a difference between two temperatures only a few degrees apart, some of the error in the thermometer tends to cancel out. Suppose, for instance, that the true value of t , is 24.00 C and the measured value is 25.15 .C. Then, suppose that the true value of tzw is 26.00 C and the measured value is 27.20. The error in tow - $1w would be only 0.05 C. But, of course, some of the resistance thermometers are not this accurate, and there are a number of other sources of error. You will probably be using a liquid-in-glass thermometer for reading the temperature of the boiling water. It may be slightly different from 100 C due to non-standard atmospheric pressure or to impurities in the water. The high temperature could damage some types of resistance thermometers. Apparatus Calorimeter Resistance-thermometer probe Chart of temperature vs resistance for probe Digital multimeter Electric stove or immersion heater Thermometer, liquid in glass type. -20 C to + 1 10 .C Aluminum sample Other metal sample Wire with loop on end for handling samples Beaker, 1000 ml Beaker, 400 ml or 250 ml Triple-beam balance Procedure Locate the electric stove at one end of the table and the calorimeter and the resistance thermometer at the other. Fill the large beaker about three-quarters full of water. Begin heating the large beaker of water on the stove in preparation for boiling it. If you use an immersion heater, be sure it is always under water when it is receiving electric power. Weigh the aluminum cylinder on the triple-beam balance and find its mass (m,). Place the hook of the aluminum cylinder through the loop on the end of the wire. Use the wire to lower the aluminum cylinder into the hot water. Leave the cylinder standing in the beaker with its hook upward, so that you can easily remove the cylinder from the boiling water later. Be sure the cylinder does not touch the immersion heater. Be sure that the resistance thermometer probe is dry and that it is far away from the electric stove. Prop the probe with the tip in the air and not touching the table or other objects. Plug its black wire into the jack of the digital multimeter marked "COM". Plug the red lead from the probe into the jack marked Be sure Press the button marked "k(2" and the button marked "200 k$2". Find the roomtemperature to the nearest . 1 .C with your own resistance thermometer. Read the resistance on the digital multimeter and use the temperature conversion chart. Weigh the empty calorimeter cup. Then fill the cup about three-quarters full of water at a temperature a few degrees below room temperature. (If the tap water or other water provided in the laboratory is not cool enough, mix some of it with water from the drinking fountain.) Weigh the cup again and subtract the mass of the empty container to find the mass of the water mw- Remove the split rubber stopper from the calorimeter and install the resistance-thermometer probe through the hole in the stopper. Reinstall the stopper and thermometer probe in the calorimeter. After the metal sample (i.c., the aluminum cylinder) has been in the boiling water for at least 5 minutes, measure and record the temperature of the boiling water with the -20 to + 110 OC glass thermometer. Record this temperature as the initial temperature of the metal sample ($1s). But do not use the same thermometer probe as is being used for measurements in the calorimeter. The initial temperature of the water in the calorimeter cup should be about 2.0 Co below room temperature. If the temperature is too low, raise the temperature by grasping the inner cup with your hand. When the temperature is within a few tenths of a degree of the correct starting temperature, allow the water temperature to rise slowly and naturally (without warming the cup with your hand). Stir the water frequently to keep the temperature uniform; but do not stir so vigorously as to slosh water out of the inner cup. When the water temperature is approximately correct, measure it with the resistance thermometer and chart. Record this temperature to the nearest ,01 or .02 OC as 1 1w- Use the wire with the loop on the end and transfer the metal sample from the boiling water to the calorimeter water. Shake off drops of hot water clinging to the metal sample before placing it in the calorimeter; but keep the time for the transfer to a minimum. The calorimeter may be moved near the boiling water temporarily during the transfer of the metal sample; but be sure that the calorimeter is remote from the boiling water before and after the transfer. Stir the water in the calorimeter continuously, but not so vigorously as to splash water out of the inner cup. Temperature measurements taken during the first two minutes may not be very meaningful. Continue stirring the calorimeter water after the first two minutes while observing the thermometer to determine the highest temperature reached (corresponding to the lowest resistance). Record this temperature as tow to the nearest .01 or .02 OC. Calculate the heat added to the calorimeter using equation (2). Then calculate the specific heat of the metal sample using equation (3). The lab instructor will provide you with the value of the water equivalent (me) of the calorimeter cup and stirrers Look up the accepted value of the specific heat of the metal sample in a textbook or handbook of chemistry or physics. Calculate the percent error in your measurement of the specific heat. Repeat steps I through 12 for the second metal sample. Be sure to record the type of metal on your data sheet for both samples. Note that it will be necessary to replace the water in the calorimeter cup and to reweigh it. The initial water temperature in the calorimeter cup should be about 1.0 Co below room temperature for the second sample (not aluminum). The room temperature should be remeasured. Shut off electric power to the stove or to the immersion heater when finished.Questions 1. Why is it important that the same thermometer be kept in the calorimeter for the entire experiment? 2. Judging from the results, is radiant heat loss a significant factor? 3. How would the computed value of specific heat be affected if some boiling water were carried over to the calorimeter with the metal sample