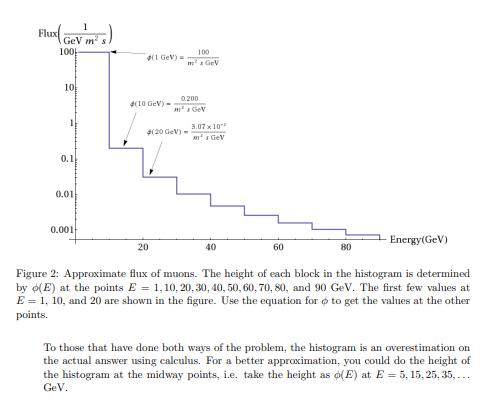
In the lecture, Professor Murayama talked about how we can use cosmic ray muons to map otherwise invisible things. A particularly novel example he discussed was Luis Alvarez looking for a hidden chamber in an Egyptian pyramid. In this problem we explore the basic idea a bit further. Muons, since they are charged, lose energy as they pass through material. Energetic muons (1000 GeV E 1 GeV) are in the so-called "minimum ionizing case" where they lose a constant amount of energy for most of their passage. Just before they stop, they rapidly lose their enery (just like the protons of last week's proton beam therapy question). If you want to see a plot of energy loss per distance of muons as a function of energy, see figure 30.1 (page 4) here: http://pdg.lbl.gov/2013/reviews/rpp2012-rev-passage-particles-matter.pdf In the minimum ionizing case, the "stopping power" of a material on muons is MeV cm dE dr 2. g (don't worry about the derivative sign-calculus is not required for this problem unless you want!). What stopping power means is that for a given density of material, px dE is the energy lost per distance of the muon passing through the material (check the units to make sure this is the case!). We will do some warm up in parts (a) and (b) of this problem to make sure we understand how to work with the quantities given and what they mean. In part (c) we utilize the same concepts in a more realistic (yet challenging) scenario. (a) How far will a 100 GeV muon travel through rock? Take the density of rock to be 2.7 g/cm and give your answer to two significant figures. (b) Now imagine you have three different detectors as shown in figure 1. Each detector has an area of 1 m. We will be asking how many muons reach each detector. Imagine the flux of muons (here flux = number per area per time per energy, area time energy) to be constant # up to 100 GeV, and then zero for energies above that. 100 m 28-GeV-1 0 for E < 100 GeV for E 100 GeV (note that this constant flux in energy is not true in the real world see the optional part of this problem). How many muons reach detectors (B) and (C) after one hour? As is often the case, dimensional analysis provides the guidance for setting up the necessary equation. Give your answer to two significant figures. Hint: If you do this for detector A, you get Ndetect. A = 3.6 x 107 muons. If you need a further hint, online in the quiz feedback, I show the steps for calculating the answer for detector A. mim P-3 plom P-2 g/m H 50 m B 25 m P P 25 m Figure 1: Muons impingent on three different detectors. Each detector has an area of 1 m. In (A) there is no material above the detector. Detector (B) is beneath 50 m of rock with a density of p1 = 3 g/cm. Detector (C) is beneath a tower of two different types of rock, p1 = 3 g/cm and p = 2 g/cm (c) Note: below are two variations of the same problem. One requires calculus, the other doesn't. Either answer will be graded as correct. The actual flux is energy dependent, decreasing with energy as ox E-27. For concrete- ness, the flux is 7 (GEV) 27 for E> 1 GeV 100 m s GeV where E is the energy measured in GeV (so that at E = 1 GeV the flux is the value used in part (b) of the problem). Variation of problem requiring calculus: Using the flux equation above, how many muons with initial energies between 1 and 100 GeV reach detectors (B) and (C) after one hour? Give your answer to two significant figures. Hints/tips/possible problems: If we were really doing this properly, we should specify a detector resolution, i.e. what range of muon energies can our detector measure. We won't worry about this (I've avoided this problem by not asking you about the flux at detector A where you might notice a problem if you tried to send the energy to zero, as well as by asking you only about the flux for given range of initial energies not their energies at the detector). As a check so you don't need to worry about if you are entering answers into the website correctly, if we let the maximum initial energy extend from 100 GeV to infinity, you would find 653 muons at detector B after one hour. Variation of problem without calculus: An approximate form of the muon flux is shown in figure 2. Using this graph, how many muons reach detectors (B) and (C) after one hour? Give your answer to two signficant figures. Hint: part (b) of this problem is like having the histogram at the height of my for 1 GeV < E < 100 GeV. GeV Flux (Gevms) 100 10 0.1 0.01 0.001 (1 GeV) (10 GeV) - 20 100 m GeV 0.200 GeV 4(20 GeV)- 3.07x10 m s GeV 40 60 80 Energy(GeV) Figure 2: Approximate flux of muons. The height of each block in the histogram is determined by o(E) at the points E= 1, 10, 20, 30, 40, 50, 60, 70, 80, and 90 GeV. The first few values at E = 1, 10, and 20 are shown in the figure. Use the equation for to get the values at the other points. To those that have done both ways of the problem, the histogram is an overestimation on the actual answer using calculus. For a better approximation, you could do the height of the histogram at the midway points, i.e. take the height as o(E) at E= 5, 15, 25, 35, GeV.