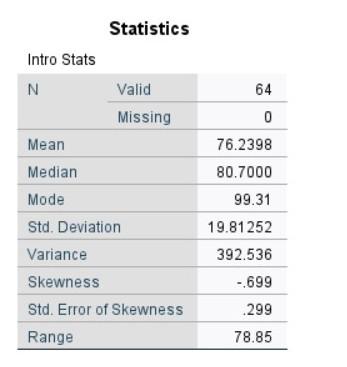
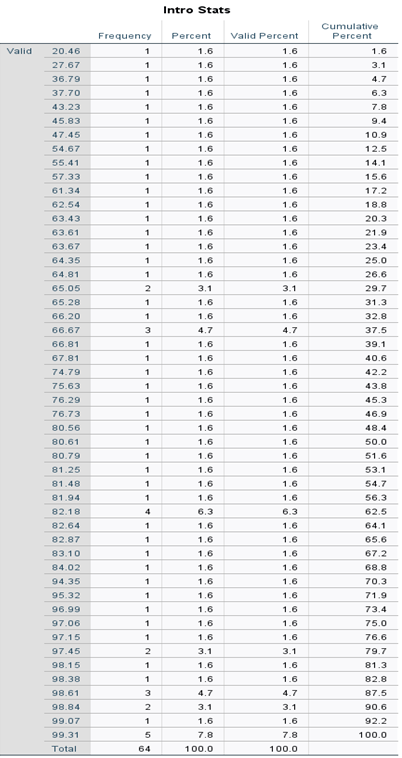
Hypothesis Testing with z Tests The general purpose for this set of exercises is to provide hands-on experience testing the null hypothesis with z tests. Launch SPSS. We will create a new data set where the scores come from students in an introductory statistics class. Create a variable called "Intro_Stats" and enter these data for their grades: HYPOTHESIS TESTING WITH z TESTS We can now refer to these students as a sample of students in introductory statistics. The goal here is to see if students in an introductory statistics class have different scores than students in all statistics courses. Let us walk through the six steps to hypothesis testing for this dataset. Step 1: Identify the population, comparison distribution, and assumptions There are two populations. The first population is students in an introductory statistics class and the second population is students in all statistics courses. Our participants and their data points comprise a sample (selected from the population of introductory statistics students). The comparison distribution is a distribution of all possible means of samples selected from the population of students in all statistics courses. The three assumptions seem to be met. The dependent variable is a scale variable, the sample of students was randomly selected (let us say we are the researchers and did randomly select the sample), and the central limit theorem tells us that the third assumption is likely met. Step 2: State the null and research hypotheses Consistent with the standard in the field, we will use a non-directional hypothesis. Thus, we are not making any conclusions as to whether the introductory course scored higher or lower than the advanced course. HYPOTHESIS TESTING WITH z TESTS S-43 Step 3: Determine the characteristics of the comparison distribution Assume that this is the mean and standard deviation for all statistics courses: =75.43=9.18 Remember that the standard error is used for the z statistic and calculated from the standard deviation divided by the square root of the sample size. Step 4: Determine the critical values or cutoffs A positive to using z tests is, as z scores are a standardized measure, the critical value does not change, assuming we apply the same p level cutoff. Using the typical .05 cutoff, the critical values are 1.96 and 1.96. Step 5: Calculate the test statistic Finally, we get to use SPSS, albeit briefly. Do you recall how to find a variable's mean? While this is a seemingly miniscule use of SPSS for this task, it is a simple demonstration of the benefits of using a statistical computer package. Although many statistical tests can be completed by hand, such as statistics using z scores, the calculations become complex and time-consuming. In this case, we learned how to calculate the mean Step 4: Determine the critical values or cutoffs A positive to using z tests is, as z scores are a standardized measure, the critical value does not change, assuming we apply the same p level cutoff. Using the typical .05 cutoff, the critical values are 1.96 and 1.96. Step 5: Calculate the test statistic Finally, we get to use SPSS, albeit briefly. Do you recall how to find a variable's mean? While this is a seemingly miniscule use of SPSS for this task, it is a simple demonstration of the benefits of using a statistical computer package. Although many statistical tests can be completed by hand, such as statistics using z scores, the calculations become complex and time-consuming. In this case, we learned how to calculate the mean (and other descriptive statistics), but do we really want to calculate the mean for 64 values? And 64 is on the low end of the number of data points one is likely to have in a real experiment (the example in the text used a sample of 1000). To avoid doing this calculation by hand, complete the steps from previous labs to get the descriptive statistics. Use the Z Statistic formula to calculate a Z statistic. Remember you must calculate the standard error for your z statistic formula. Step 6:Makeadecision Compare your Z statisitic with the critical values listed in Step 4 ave you OUTPUT file and turn in OUTPUT file along with your answers to the uestions below, in your own words, via email to me before lab time next Monday QUESTIONS 1. Report the following from your data: a. M= ? b. SD= ? c. Skewness = ? d. z= ? e. M= ? 2. State the null hypotheses and research hypothesis. 3. State your conclusions related to the null hypothesis based on your data analysis. 4. What is the percentile rank of this sample of intro stats students data you entered? Statistics Intro Stats Intro Stats Hypothesis Testing with z Tests The general purpose for this set of exercises is to provide hands-on experience testing the null hypothesis with z tests. Launch SPSS. We will create a new data set where the scores come from students in an introductory statistics class. Create a variable called "Intro_Stats" and enter these data for their grades: HYPOTHESIS TESTING WITH z TESTS We can now refer to these students as a sample of students in introductory statistics. The goal here is to see if students in an introductory statistics class have different scores than students in all statistics courses. Let us walk through the six steps to hypothesis testing for this dataset. Step 1: Identify the population, comparison distribution, and assumptions There are two populations. The first population is students in an introductory statistics class and the second population is students in all statistics courses. Our participants and their data points comprise a sample (selected from the population of introductory statistics students). The comparison distribution is a distribution of all possible means of samples selected from the population of students in all statistics courses. The three assumptions seem to be met. The dependent variable is a scale variable, the sample of students was randomly selected (let us say we are the researchers and did randomly select the sample), and the central limit theorem tells us that the third assumption is likely met. Step 2: State the null and research hypotheses Consistent with the standard in the field, we will use a non-directional hypothesis. Thus, we are not making any conclusions as to whether the introductory course scored higher or lower than the advanced course. HYPOTHESIS TESTING WITH z TESTS S-43 Step 3: Determine the characteristics of the comparison distribution Assume that this is the mean and standard deviation for all statistics courses: =75.43=9.18 Remember that the standard error is used for the z statistic and calculated from the standard deviation divided by the square root of the sample size. Step 4: Determine the critical values or cutoffs A positive to using z tests is, as z scores are a standardized measure, the critical value does not change, assuming we apply the same p level cutoff. Using the typical .05 cutoff, the critical values are 1.96 and 1.96. Step 5: Calculate the test statistic Finally, we get to use SPSS, albeit briefly. Do you recall how to find a variable's mean? While this is a seemingly miniscule use of SPSS for this task, it is a simple demonstration of the benefits of using a statistical computer package. Although many statistical tests can be completed by hand, such as statistics using z scores, the calculations become complex and time-consuming. In this case, we learned how to calculate the mean Step 4: Determine the critical values or cutoffs A positive to using z tests is, as z scores are a standardized measure, the critical value does not change, assuming we apply the same p level cutoff. Using the typical .05 cutoff, the critical values are 1.96 and 1.96. Step 5: Calculate the test statistic Finally, we get to use SPSS, albeit briefly. Do you recall how to find a variable's mean? While this is a seemingly miniscule use of SPSS for this task, it is a simple demonstration of the benefits of using a statistical computer package. Although many statistical tests can be completed by hand, such as statistics using z scores, the calculations become complex and time-consuming. In this case, we learned how to calculate the mean (and other descriptive statistics), but do we really want to calculate the mean for 64 values? And 64 is on the low end of the number of data points one is likely to have in a real experiment (the example in the text used a sample of 1000). To avoid doing this calculation by hand, complete the steps from previous labs to get the descriptive statistics. Use the Z Statistic formula to calculate a Z statistic. Remember you must calculate the standard error for your z statistic formula. Step 6:Makeadecision Compare your Z statisitic with the critical values listed in Step 4 ave you OUTPUT file and turn in OUTPUT file along with your answers to the uestions below, in your own words, via email to me before lab time next Monday QUESTIONS 1. Report the following from your data: a. M= ? b. SD= ? c. Skewness = ? d. z= ? e. M= ? 2. State the null hypotheses and research hypothesis. 3. State your conclusions related to the null hypothesis based on your data analysis. 4. What is the percentile rank of this sample of intro stats students data you entered? Statistics Intro Stats Intro Stats