I am doing this work through SPSS and I am confused in regards to the two graphs as far as which one to include in my report and as far as mentioning the extreme outliers. I am not sure that if this information is incorrect, then everything else is incorrect.

Also besides that part, is the description of statistics, assumption of normality, assumption of Homogeneity of variance, and results correct?

thank you.

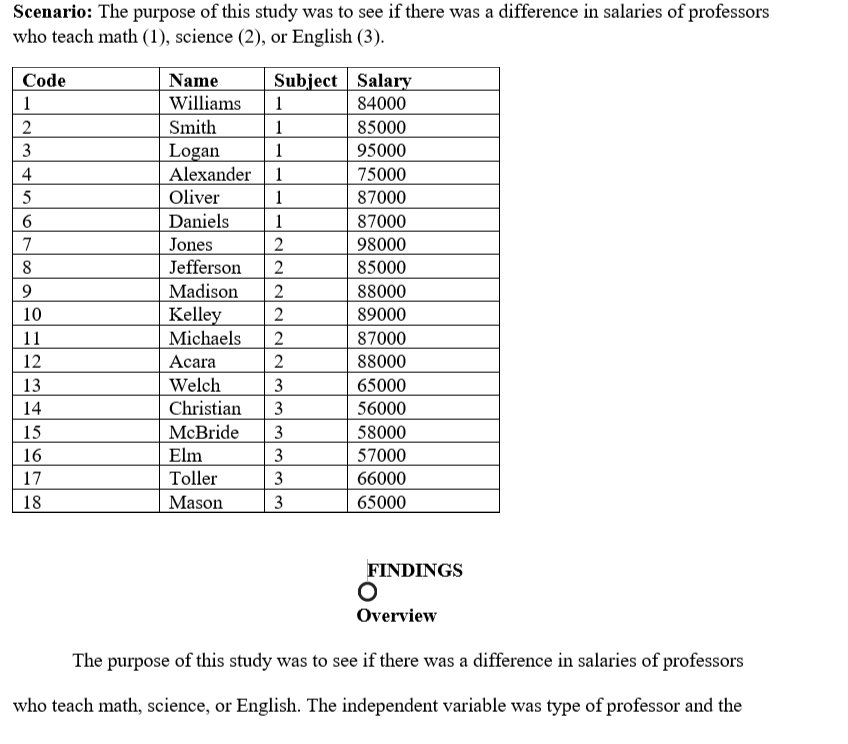
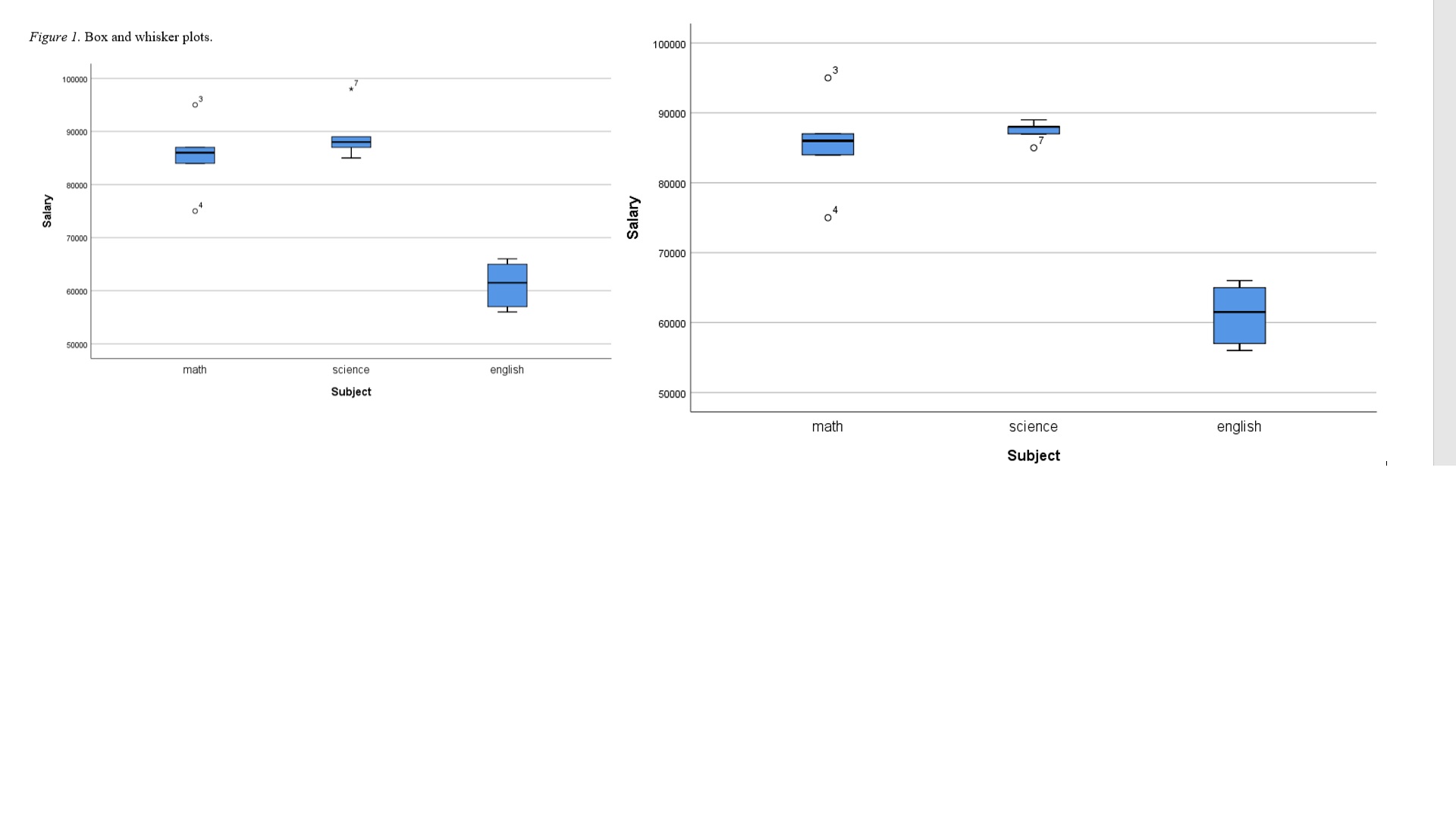
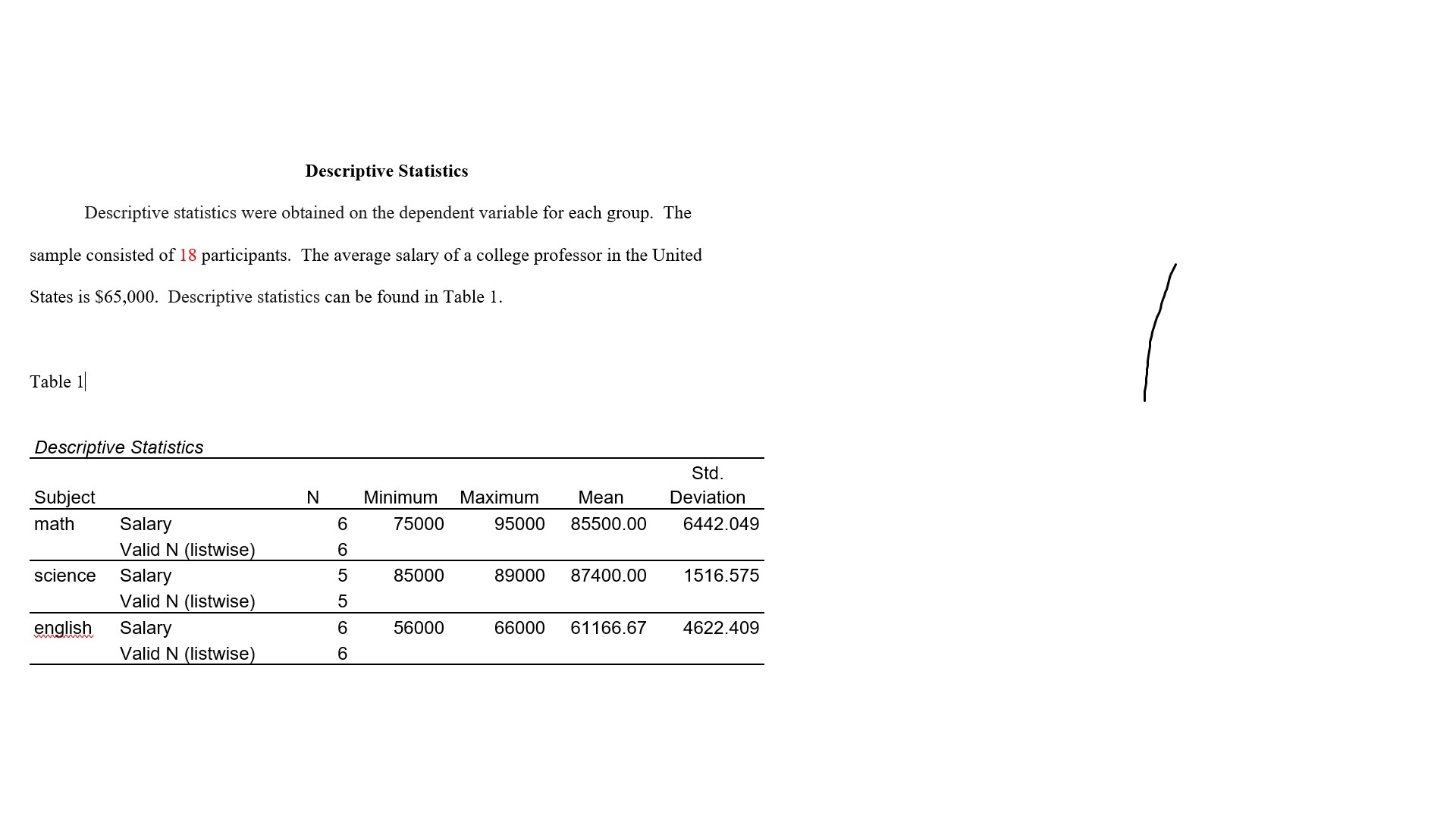
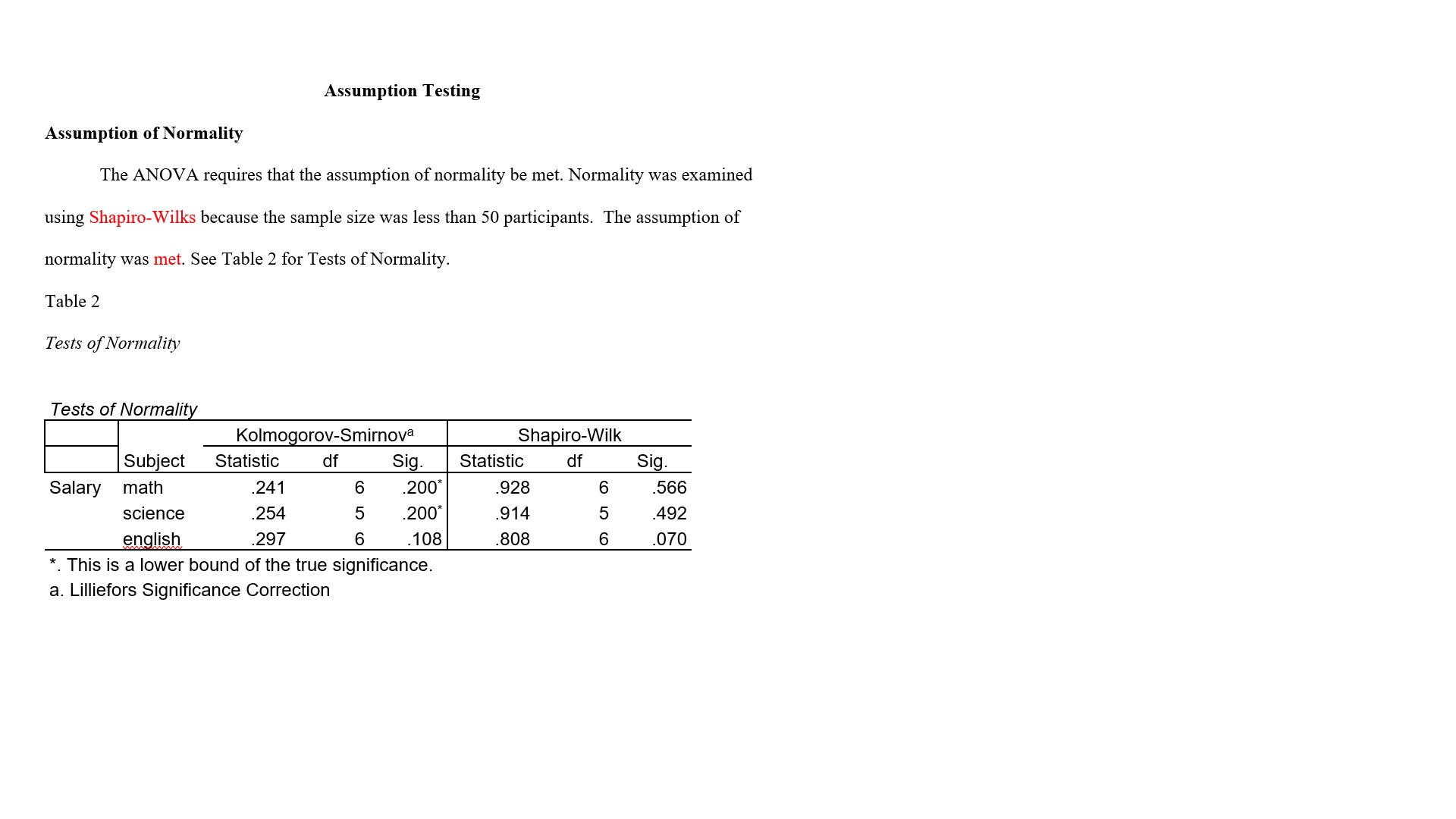
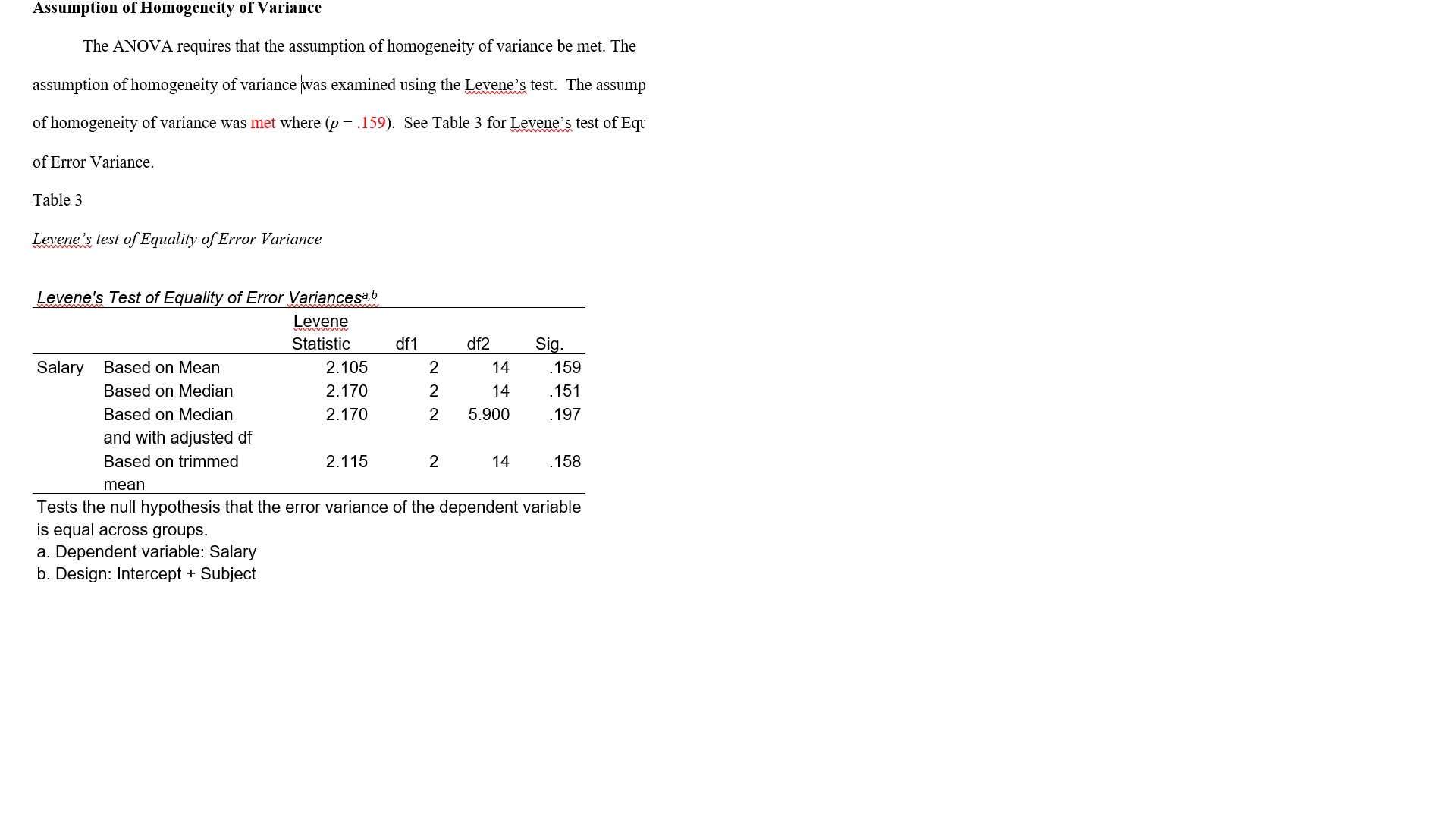
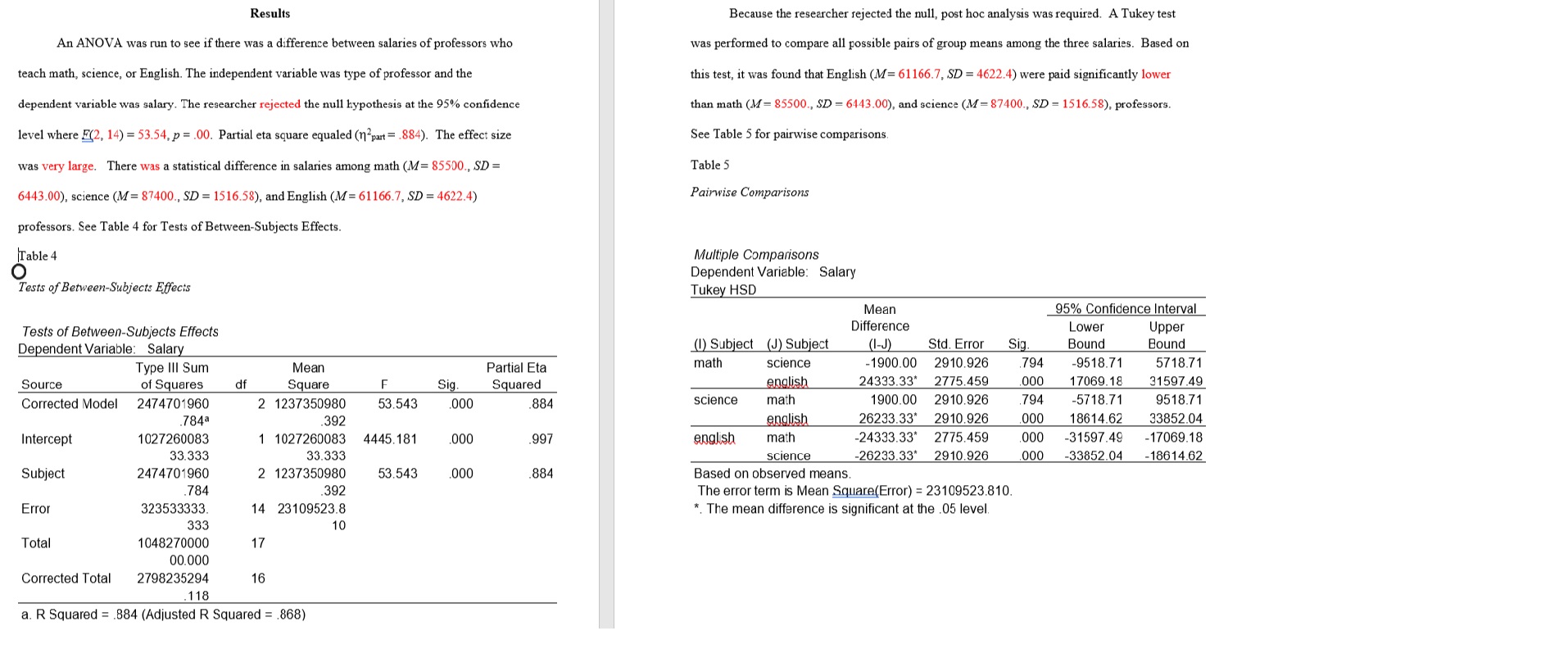
Scenario: The purpose of this study was to see if there was a difference in salaries of professors who teach math (1), science (2), or English (3). Code Name Subject Salary 1 Williams 1 84000 2 Smith 85000 3 Logan 95000 VIA Alexander 75000 Oliver 87000 6 Daniels 87000 Jones 2 98000 Jefferson 85000 9 Madison 88000 10 Kelley Acara Welch W WW WW N N N N N 89000 11 Michaels 87000 12 88000 13 65000 14 Christian 56000 15 McBride 58000 16 Elm 57000 17 Toller 66000 18 Mason 3 65000 FINDINGS O Overview The purpose of this study was to see if there was a difference in salaries of professors who teach math, science, or English. The independent variable was type of professor and thedependent variable was salary. A One-way Analysis of Variance (ANOVA) was used to test the hypothesis. This Findings Section includes the research question, null hypothesis, data screening, descriptive statistics, assumption testing, and results. Research Question RQ: Is there a difference between salaries of professors who teach math, science, or English? Null Hypothesis Ho: There is no significant difference between salaries of professors who teach math, science, or English. Data Screening Data screening was conducted on each group's dependent variable. The researcher sorted the data on each variable and scanned for inconsistencies. No data errors or inconsistencies were identified. Box and whiskers plots were used to detect outliers on each dependent variable. No outliers were identified. See Figure 1 for box and whisker plots.Figure 1. Box and whisker plots. 100000 100000 Ow 03 90000 90000 I 80000 30000 Salary 0 4 Salary 04 70000 70000 60000 60000 50000 math science english Subject 50000 math science english SubjectDescriptive Statistics Descriptive statistics were obtained on the dependent variable for each group. The sample consisted of 18 participants. The average salary of a college professor in the United States is $65,000. Descriptive statistics can be found in Table 1. Table 1 Descriptive Statistics Std. Subject N Minimum Maximum Mean Deviation math Salary 6 75000 95000 85500.00 6442.049 Valid N (listwise) science Salary 85000 89000 87400.00 1516.575 Valid N (listwise) english Salary 56000 66000 61 166.67 4622.409 Valid N (listwise)Assumption Testing Assumption of Normality The ANOVA requires that the assumption of normality be met. Normality was examined using Shapiro-Wilks because the sample size was less than 50 participants. The assumption of normality was met. See Table 2 for Tests of Normality. Table 2 Tests of Normality Tests of Normality Kolmogorov-Smirnova Shapiro-Wilk Subject Statistic df Sig. Statistic df Sig Salary math 241 6 200' 928 6 566 science .254 .200' .914 .492 english 297 6 BOL 808 6 .070 *. This is a lower bound of the true significance. a. Lilliefors Significance CorrectionAssumption of Homogeneity of Variance The ANOVA requires that the assumption of homogeneity of variance be met. The assumption of homogeneity of variance was examined using the Levene's test. The assump of homogeneity of variance was met where (p = .159). See Table 3 for Levene's test of Equ of Error Variance. Table 3 Levene's test of Equality of Error Variance Levene's Test of Equality of Error Variancesa.b Levene Statistic df1 df2 Sig Salary Based on Mean 2. 105 N 14 . 159 Based on Median 2.170 NN 14 . 151 Based on Median 2. 170 5.900 197 and with adjusted df Based on trimmed 2.115 2 14 . 158 mean Tests the null hypothesis that the error variance of the dependent variable is equal across groups. a. Dependent variable: Salary b. Design: Intercept + SubjectResults Because the researcher rejected the null, post hoc analysis was required. A Tukey test An ANOVA was run to see if there was a difference between salaries of professors who was performed to compare all possible pairs of group means among the three salaries. Based on teach math, science, or English. The independent variable was type of professor and the this test, it was found that English (M= 61166.7, SD = 4622.4) were paid significantly lower dependent variable was salary. The researcher rejected the null hypothesis at the 95% confidence than math (M= 85500., SD = 6443.00), and science (M= 87400., SD = 1516.58), professors. level where F(2, 14) = 53.54, p = .00. Partial eta square equaled (1 part = .884). The effect size See Table 5 for pairwise comparisons. was very large. There was a statistical difference in salaries among math (M= 85500., SD = Table 5 6443.00), science (M= 87400., SD = 1516.58), and English (M= 61166.7, SD = 4622.4) Pairwise Comparisons professors. See Table 4 for Tests of Between-Subjects Effects. Table 4 Multiple Comparisons O Dependent Variable: Salary Tests of Between-Subjects Effects Tukey HSD Mean 95% Confidence Interval Tests of Between-Subjects Effects Difference Lower Upper Dependent Variable: Salary (1) Subject (J) Subject (1 -J) Std. Error Sig Bound Bound Type Ill Sum Mean Partial Eta math science 1900.00 2910.926 794 -9518.71 5718.71 Source of Squares Square F Sig. Squared english 24333.33* 2775.459 000 17069.18 31597.49 Corrected Model 2474701960 1237350980 53.543 000 884 science math 1900.00 2910.926 794 -5718.71 9518.71 784a 392 english 26233.33* 2910.926 000 18614.62 33852.04 Intercept 1027260083 1 1027260083 4445. 181 000 997 english math -24333.33* 2775.459 000 31597.49 -17069.18 33.333 33.333 science -26233.33 2910.926 .000 -33852.04 -18614.62 Subject 2474701960 2 1237350980 53.543 000 884 Based on observed means. 784 392 The error term is Mean Square(Error) = 23109523.810. Error 323533333. 14 23109523.8 *. The mean difference is significant at the .05 level. 333 10 Total 1048270000 17 00.000 Corrected Total 2798235294 16 118 a. R Squared = .884 (Adjusted R Squared = .868)