i am having trouble with a homework assignment. specifically with part C-F. please help!

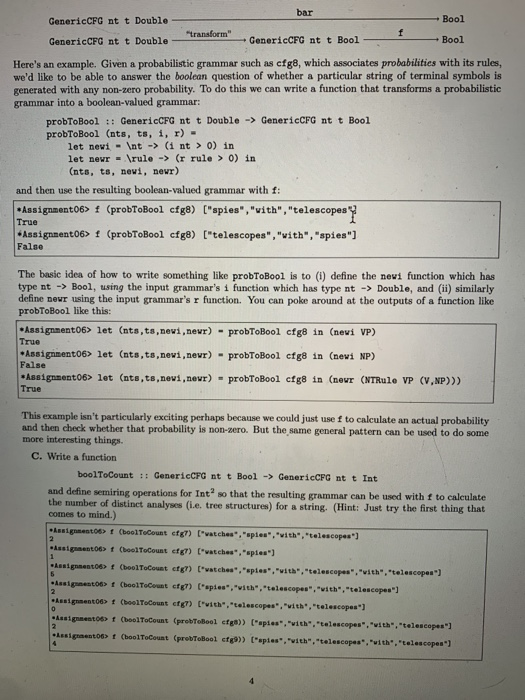
table-based memoization. You can essentially ignore it-I'll make sure that all the types you need to use do satisfy this requirement. (See e.g. the deriving Ord on our declaration of the Cat type.) 1 Leftmost derivations In Assignment06.hs I've also defined a type data Treo nt t - Leaf nt t NonLeaf nt (Treo nt t) (Treo nt t) deriving Show for representing phrase-structure trees of the familiar sort, and two example trees trees and tree2. These are our Haskell representations of the following trees: VP NP VP watches VPPP NPPP spies VNP PNP PNP watches spies with telescopes with telescopes treei tree2 Recall that a derivation in a context-free grammar is a sequence of rewriting steps (see (2) and (6) on the class handout). If we restrict ourselves to derivations where each step rewrites the leftmost "unexpanded" nonterminal symbol, it turns out there's exactly one such derivation corresponding to each tree structure. These derivations are known as leftmost deriuations. Here are the leftmost derivations corresponding to tree1 and tree2; each derivation is shown in two columns, where the first column shows the rule being used at each step. VP VPVP PP VP PP VP + V NP V NP VP + V NPV NP PP V watches watches NP V watches watches NP PP NP NP PP watches NP PP NP sples watches spies PP NP-spies watches spies PP PP PNP watches spies P NP PP-PNP watches sples P NP P with watches spies with NP P with watches spies with NP NP-telescopes watches spies with telescopes NP telescopes watches spies with telescopes Notice that if you know the sequence of rules that applied in a leftmost derivation, then it's possible to reconstruct the entire derivation (i.e. the second column in one of the two derivations above). So such a sequence of rules can be taken as, in effect, another representation of a tree structure. A. Write a function treeToDeriv :: Tree nt t -> [RewriteRule nt t] which computes the list of rewrite rules, in order, that are used in the leftmost derivation corresponding to the given tree. (Hint: The left hand side of the first rule in the output list will necessarily be the same as the root nonterminal of the input tree.) Assignment06> treeToDeriv treet [NTRule VP (VP.PP), NTRule VP (V,NP), TRule V "watches". Thule NP "spies". NTRule PP (P.NP), TRule P "with", Thule NP "telescopes"] Assignment06> treeToDeriv tree2 ENTRule VP (V,NP),Thule V "watches", NTRule NP (NP.PP),TRule NP "apies", NTRule PP (PNP), TRule P "with", TRule NP "telescopes") Assignment06> treeToDeriv (Leaf P 'vith") [TRule P "with") 2 Semirings and CFGs First a relatively straightforward warm-up. B. Write a function f 1: (Ord nt, Ordt, Semiring a) -> GenericCFG nt ta -> [t] => a that computes, in a semiring-general way, the "complete" value that the given grammar assigns to the given string, i.e. taking into account what the grammar says about starting nonterminals as well as inside values. For boolean-valued grammars, this essentially amounts to (12) on this week's handout. Assignment06> f cfg7 ["watches", "spies","vith","telescopes") True Assignment06> f cfg7 ("spies", "with","telescopes") True Assignment06) f cfg7 (telescopes","vith","telescopes") False Assignment06> f cfgs ("watches","spies","vith","telescopes") 1.2e-2 *Assignment06> cfg8 ("telescopes","vith","telescopes") 0.0 Assignment06) f cfgo (watches", "spies","vith", "telescopes") 6.08-3 *Assignment06> f cfg (telescopes","vith","telescopes") 9.0-3 Assignment06> f ergo telescopes","vith","telescopes","with".spies,"with","apies) 7.200000000000002-5 Now for the more interesting part. The type of the t function tells us that whenever we pass in a grammar that has, say, booleans Associated with its rules, the value computed by f will also be a boolean, and whenever we pass in a grammar that has probabilities (Le. Doubles) sociated with its rules, the value computed by I will also be a probability. If we want to compute some different kind of thing-for example, if we want to do some calculation whose result is an Int using cfg7, or if we want to do some calculation whose result is a Bool using cfg8 - then this is not something that we can do by using f with cfg7 or cfg8 as its first argument. Maybe we'd just have to write some other functions, say called foo and bar, with these types: too :: GenericCFG nt t Bool -> Int bar :: GenericCFG nt t Double -> Bool But a neater strategy that's often available is to transform the grammar into some other grammar that has the same rules, but aociates new values of the desired type with those rules, in such a way that running our existing, flexible f function on this new grammar does just what we need. Here's a picture of the iden: foo Int GenericCFG nt t Bool- GenericCFC nt t Bool- transform am GenericCFG nt t Int bar --- Bool GenericCFG nt t Double - "transform" . GenericCFG nt t Double- GenericCFC at t Bool - - Bool Here's an example. Given a probabilistic grammar such as cfg8, which associates probabilities with its rules we'd like to be able to answer the boolean question of whether a particular string of terminal symbols is! generated with any non-zero probability. To do this we can write a function that transforms a probabilistic grammar into a boolean-valued grammar: probToBool :: GenericCFG nt t Double -> GenericCFG nt t Bool probToBool (nts, ts, 1, ) - let nevi - Int -> (int > 0) in let newr - ule -> (r rule > 0) in (nts, ts, nevi, nevr) and then use the resulting boolean-valued grammar with f: Assignment06> (probToBool cfg8) ["spies","vith","telescopes True *Assignment06> (probToBool cfg) ["telescopes", "with", "spies") False The basic idea of how to write something like probToBool is to (i) define the newi function which has type nt -> Bool, using the input grammar's i function which has type nt -> Double, and (11) similarly define Devr using the input grammar's r function. You can poke around at the outputs of a function like probToBool like this: *Assignment06> let (nts,ts, nevi,newr) - probToBool cfg8 in (nevi VP) True Assignment06> let (nta,ta, nevi, nevr) - probToBool cfg8 in (nevi NP) False Assignment06> let (nto,ta, nevi, nevr) - probToBool cfg8 in (neur (NTRule VP (V.NP))) True This example isn't particularly exciting perhaps because we could just usef to calculate an actual probability and then check whether that probability is non-zero. But the same general pattern can be used to do some more interesting things. c. Write a function boolToCount : GenericCFG at t Bool -> GenericCFG nt t Int and define semiring operations for Int so that the resulting rammar can be used with t to calculate the number of distinct analyses (le, tree structures) for a string. (Hint: Just try the first thing that comes to mind.) asi f CholToCount en watches sples""with.telescope ) e t Colocount for watches, ples") es t Chalecos en watches.plas t elescoperith, telescope *kui teel Toomas en Caples","vielescope ithelescopul t locouat en vita","telescopes".with. telescopes"] as to the Coat (probelegt)) (epies","with.telescopes","with telescope"] Chelot (pro c ) L'aples""vitelescopes with al l D. Write a function probToProblist :: GenericCFG nt t Double -> GenericCFG nt t (Double) and define semiring operations for (Double) so that the resulting grammar can be used with t to calculate the probabilities of the individual tree structures for a string. So if there is only one tree structure for the given string, then the result should be a one-element list containing the probability of that tree structure, which will also be the probability of the string itself: if there are multiple tree structures for the given string, there should be one probability for each. The order in which the probabilities appear in this list is not important. asinsent06> f (probToProblist cfg8) ["watches","apies","with","telescopes") [4.8000000000000004-3,7.2000000000000010-3] Assigngent06> f (probToProblist cfg8) ["watches","spies","with","telescopes","with","telescopes") [2.88e-4,2.88e-4.4.3200000000000004-4,4.3200000000000004-4,6.48-4) Assignment06) f (probToProblist cfgo) (apies","with","telescopes","with","telescopes") [5.4e-4,8.0999999999999982-4) Assinant06> f (probToProblist cf 9) (apies","vith", "telescopes". with","telescopes") [2.7e-4.4.049999999999999-4,3.6-4,3.6-4) Notice that the length of the list should be the same number is we can calculate using boolToCount, and the sum of the probabilities in the list should be the same number as we would get be running on the original probabilistic grammar. These are actually useful hints. - Assignment06> (probToProblist cfgs) ["vatches","spies","pth","telescopes"] [4.80000000000000040-3.7.200000000000001e-3) Assignment06) sun (f (probToProblist ofg8) ["watches","spies","vith","telescopes")) 1.2e-2 Assignment06> f cfg8 ["watches", "spies","vith","telescopes") 1.2e-2 Assignment06> (boolToCount (probTobool cfgl)) (watches","spies","vith","telescopes") E. Write a function bool ToDerivList :: GenericCFG nt t Bool -> GenericCFG nt t [RewriteRule nt t]] and define semiring operations for [RewriteRule nt t]] so that the resulting grammar can be used with 1 to find the rule sequences used in the leftmost derivations of a string. Since the rule sequence for a single derivation has type [RewriteRule), a list of such rule sequences has type C[RewriteRule nt t]). The order in which the rule sequences appear in the list does not mat- ter. The length of this list should, once again, be the same as the number of distinct derivations of the given string. The mechanism here is really the same as what we saw with output strings on FSAs; don't get distracted by the fact that we're producing lists of rules, it's just an output alphabet. Note that the order of the three elements that are "generalized-conjoined" in inside will play a role here. Assignment06> { boolToDerivit c ) ["watches, spies".with.telescopes") CONTRul. VP (V.NP).Thule V "watches".NTRule NP (NP.PP).Trul. NP "apien. NTRule PP ( PNP). Trale P "with Thule NP "telescopes"). ONTRule VP (VP.PP), NTrul. VP (V,NP), TRule V "watches", Trul. NP "epies". NT ul. PP (PNP). TRule P "with Thule NP "telescopes"]] Assignment06) f (boolToDerivList (probToBool ctg8)) (apica", "with","telescopes") CONTRule VP (VP.PP). Tule VP spies", Tal. PP ( PNP) TRule P *with". Thule NP "telescopes"]] Assignment06> f (boolToDerivlist (probToBool of 9)) (epies","with". telescopes") CENTRule VP (VP, PP), Thule VP spies", TalPP ( PNP). Thule P "with". Thule NP telescopes"). ENTRulNP (NP.PP), Thule NP spies", Tal. PP ( PNP). Thule P "with". Thule NP telescopea"]] (This output won't be neatly formatted like this, I've just tried to make it readable.) F. Write a function This means that you have to add a instance Semiring Int block. See Semiring .ha for some examples What other things could we do if the order there was different? Why does this question of how to order those conjuncts only arise for CFGs and not for FSAs? table-based memoization. You can essentially ignore it-I'll make sure that all the types you need to use do satisfy this requirement. (See e.g. the deriving Ord on our declaration of the Cat type.) 1 Leftmost derivations In Assignment06.hs I've also defined a type data Treo nt t - Leaf nt t NonLeaf nt (Treo nt t) (Treo nt t) deriving Show for representing phrase-structure trees of the familiar sort, and two example trees trees and tree2. These are our Haskell representations of the following trees: VP NP VP watches VPPP NPPP spies VNP PNP PNP watches spies with telescopes with telescopes treei tree2 Recall that a derivation in a context-free grammar is a sequence of rewriting steps (see (2) and (6) on the class handout). If we restrict ourselves to derivations where each step rewrites the leftmost "unexpanded" nonterminal symbol, it turns out there's exactly one such derivation corresponding to each tree structure. These derivations are known as leftmost deriuations. Here are the leftmost derivations corresponding to tree1 and tree2; each derivation is shown in two columns, where the first column shows the rule being used at each step. VP VPVP PP VP PP VP + V NP V NP VP + V NPV NP PP V watches watches NP V watches watches NP PP NP NP PP watches NP PP NP sples watches spies PP NP-spies watches spies PP PP PNP watches spies P NP PP-PNP watches sples P NP P with watches spies with NP P with watches spies with NP NP-telescopes watches spies with telescopes NP telescopes watches spies with telescopes Notice that if you know the sequence of rules that applied in a leftmost derivation, then it's possible to reconstruct the entire derivation (i.e. the second column in one of the two derivations above). So such a sequence of rules can be taken as, in effect, another representation of a tree structure. A. Write a function treeToDeriv :: Tree nt t -> [RewriteRule nt t] which computes the list of rewrite rules, in order, that are used in the leftmost derivation corresponding to the given tree. (Hint: The left hand side of the first rule in the output list will necessarily be the same as the root nonterminal of the input tree.) Assignment06> treeToDeriv treet [NTRule VP (VP.PP), NTRule VP (V,NP), TRule V "watches". Thule NP "spies". NTRule PP (P.NP), TRule P "with", Thule NP "telescopes"] Assignment06> treeToDeriv tree2 ENTRule VP (V,NP),Thule V "watches", NTRule NP (NP.PP),TRule NP "apies", NTRule PP (PNP), TRule P "with", TRule NP "telescopes") Assignment06> treeToDeriv (Leaf P 'vith") [TRule P "with") 2 Semirings and CFGs First a relatively straightforward warm-up. B. Write a function f 1: (Ord nt, Ordt, Semiring a) -> GenericCFG nt ta -> [t] => a that computes, in a semiring-general way, the "complete" value that the given grammar assigns to the given string, i.e. taking into account what the grammar says about starting nonterminals as well as inside values. For boolean-valued grammars, this essentially amounts to (12) on this week's handout. Assignment06> f cfg7 ["watches", "spies","vith","telescopes") True Assignment06> f cfg7 ("spies", "with","telescopes") True Assignment06) f cfg7 (telescopes","vith","telescopes") False Assignment06> f cfgs ("watches","spies","vith","telescopes") 1.2e-2 *Assignment06> cfg8 ("telescopes","vith","telescopes") 0.0 Assignment06) f cfgo (watches", "spies","vith", "telescopes") 6.08-3 *Assignment06> f cfg (telescopes","vith","telescopes") 9.0-3 Assignment06> f ergo telescopes","vith","telescopes","with".spies,"with","apies) 7.200000000000002-5 Now for the more interesting part. The type of the t function tells us that whenever we pass in a grammar that has, say, booleans Associated with its rules, the value computed by f will also be a boolean, and whenever we pass in a grammar that has probabilities (Le. Doubles) sociated with its rules, the value computed by I will also be a probability. If we want to compute some different kind of thing-for example, if we want to do some calculation whose result is an Int using cfg7, or if we want to do some calculation whose result is a Bool using cfg8 - then this is not something that we can do by using f with cfg7 or cfg8 as its first argument. Maybe we'd just have to write some other functions, say called foo and bar, with these types: too :: GenericCFG nt t Bool -> Int bar :: GenericCFG nt t Double -> Bool But a neater strategy that's often available is to transform the grammar into some other grammar that has the same rules, but aociates new values of the desired type with those rules, in such a way that running our existing, flexible f function on this new grammar does just what we need. Here's a picture of the iden: foo Int GenericCFG nt t Bool- GenericCFC nt t Bool- transform am GenericCFG nt t Int bar --- Bool GenericCFG nt t Double - "transform" . GenericCFG nt t Double- GenericCFC at t Bool - - Bool Here's an example. Given a probabilistic grammar such as cfg8, which associates probabilities with its rules we'd like to be able to answer the boolean question of whether a particular string of terminal symbols is! generated with any non-zero probability. To do this we can write a function that transforms a probabilistic grammar into a boolean-valued grammar: probToBool :: GenericCFG nt t Double -> GenericCFG nt t Bool probToBool (nts, ts, 1, ) - let nevi - Int -> (int > 0) in let newr - ule -> (r rule > 0) in (nts, ts, nevi, nevr) and then use the resulting boolean-valued grammar with f: Assignment06> (probToBool cfg8) ["spies","vith","telescopes True *Assignment06> (probToBool cfg) ["telescopes", "with", "spies") False The basic idea of how to write something like probToBool is to (i) define the newi function which has type nt -> Bool, using the input grammar's i function which has type nt -> Double, and (11) similarly define Devr using the input grammar's r function. You can poke around at the outputs of a function like probToBool like this: *Assignment06> let (nts,ts, nevi,newr) - probToBool cfg8 in (nevi VP) True Assignment06> let (nta,ta, nevi, nevr) - probToBool cfg8 in (nevi NP) False Assignment06> let (nto,ta, nevi, nevr) - probToBool cfg8 in (neur (NTRule VP (V.NP))) True This example isn't particularly exciting perhaps because we could just usef to calculate an actual probability and then check whether that probability is non-zero. But the same general pattern can be used to do some more interesting things. c. Write a function boolToCount : GenericCFG at t Bool -> GenericCFG nt t Int and define semiring operations for Int so that the resulting rammar can be used with t to calculate the number of distinct analyses (le, tree structures) for a string. (Hint: Just try the first thing that comes to mind.) asi f CholToCount en watches sples""with.telescope ) e t Colocount for watches, ples") es t Chalecos en watches.plas t elescoperith, telescope *kui teel Toomas en Caples","vielescope ithelescopul t locouat en vita","telescopes".with. telescopes"] as to the Coat (probelegt)) (epies","with.telescopes","with telescope"] Chelot (pro c ) L'aples""vitelescopes with al l D. Write a function probToProblist :: GenericCFG nt t Double -> GenericCFG nt t (Double) and define semiring operations for (Double) so that the resulting grammar can be used with t to calculate the probabilities of the individual tree structures for a string. So if there is only one tree structure for the given string, then the result should be a one-element list containing the probability of that tree structure, which will also be the probability of the string itself: if there are multiple tree structures for the given string, there should be one probability for each. The order in which the probabilities appear in this list is not important. asinsent06> f (probToProblist cfg8) ["watches","apies","with","telescopes") [4.8000000000000004-3,7.2000000000000010-3] Assigngent06> f (probToProblist cfg8) ["watches","spies","with","telescopes","with","telescopes") [2.88e-4,2.88e-4.4.3200000000000004-4,4.3200000000000004-4,6.48-4) Assignment06) f (probToProblist cfgo) (apies","with","telescopes","with","telescopes") [5.4e-4,8.0999999999999982-4) Assinant06> f (probToProblist cf 9) (apies","vith", "telescopes". with","telescopes") [2.7e-4.4.049999999999999-4,3.6-4,3.6-4) Notice that the length of the list should be the same number is we can calculate using boolToCount, and the sum of the probabilities in the list should be the same number as we would get be running on the original probabilistic grammar. These are actually useful hints. - Assignment06> (probToProblist cfgs) ["vatches","spies","pth","telescopes"] [4.80000000000000040-3.7.200000000000001e-3) Assignment06) sun (f (probToProblist ofg8) ["watches","spies","vith","telescopes")) 1.2e-2 Assignment06> f cfg8 ["watches", "spies","vith","telescopes") 1.2e-2 Assignment06> (boolToCount (probTobool cfgl)) (watches","spies","vith","telescopes") E. Write a function bool ToDerivList :: GenericCFG nt t Bool -> GenericCFG nt t [RewriteRule nt t]] and define semiring operations for [RewriteRule nt t]] so that the resulting grammar can be used with 1 to find the rule sequences used in the leftmost derivations of a string. Since the rule sequence for a single derivation has type [RewriteRule), a list of such rule sequences has type C[RewriteRule nt t]). The order in which the rule sequences appear in the list does not mat- ter. The length of this list should, once again, be the same as the number of distinct derivations of the given string. The mechanism here is really the same as what we saw with output strings on FSAs; don't get distracted by the fact that we're producing lists of rules, it's just an output alphabet. Note that the order of the three elements that are "generalized-conjoined" in inside will play a role here. Assignment06> { boolToDerivit c ) ["watches, spies".with.telescopes") CONTRul. VP (V.NP).Thule V "watches".NTRule NP (NP.PP).Trul. NP "apien. NTRule PP ( PNP). Trale P "with Thule NP "telescopes"). ONTRule VP (VP.PP), NTrul. VP (V,NP), TRule V "watches", Trul. NP "epies". NT ul. PP (PNP). TRule P "with Thule NP "telescopes"]] Assignment06) f (boolToDerivList (probToBool ctg8)) (apica", "with","telescopes") CONTRule VP (VP.PP). Tule VP spies", Tal. PP ( PNP) TRule P *with". Thule NP "telescopes"]] Assignment06> f (boolToDerivlist (probToBool of 9)) (epies","with". telescopes") CENTRule VP (VP, PP), Thule VP spies", TalPP ( PNP). Thule P "with". Thule NP telescopes"). ENTRulNP (NP.PP), Thule NP spies", Tal. PP ( PNP). Thule P "with". Thule NP telescopea"]] (This output won't be neatly formatted like this, I've just tried to make it readable.) F. Write a function This means that you have to add a instance Semiring Int block. See Semiring .ha for some examples What other things could we do if the order there was different? Why does this question of how to order those conjuncts only arise for CFGs and not for FSAs