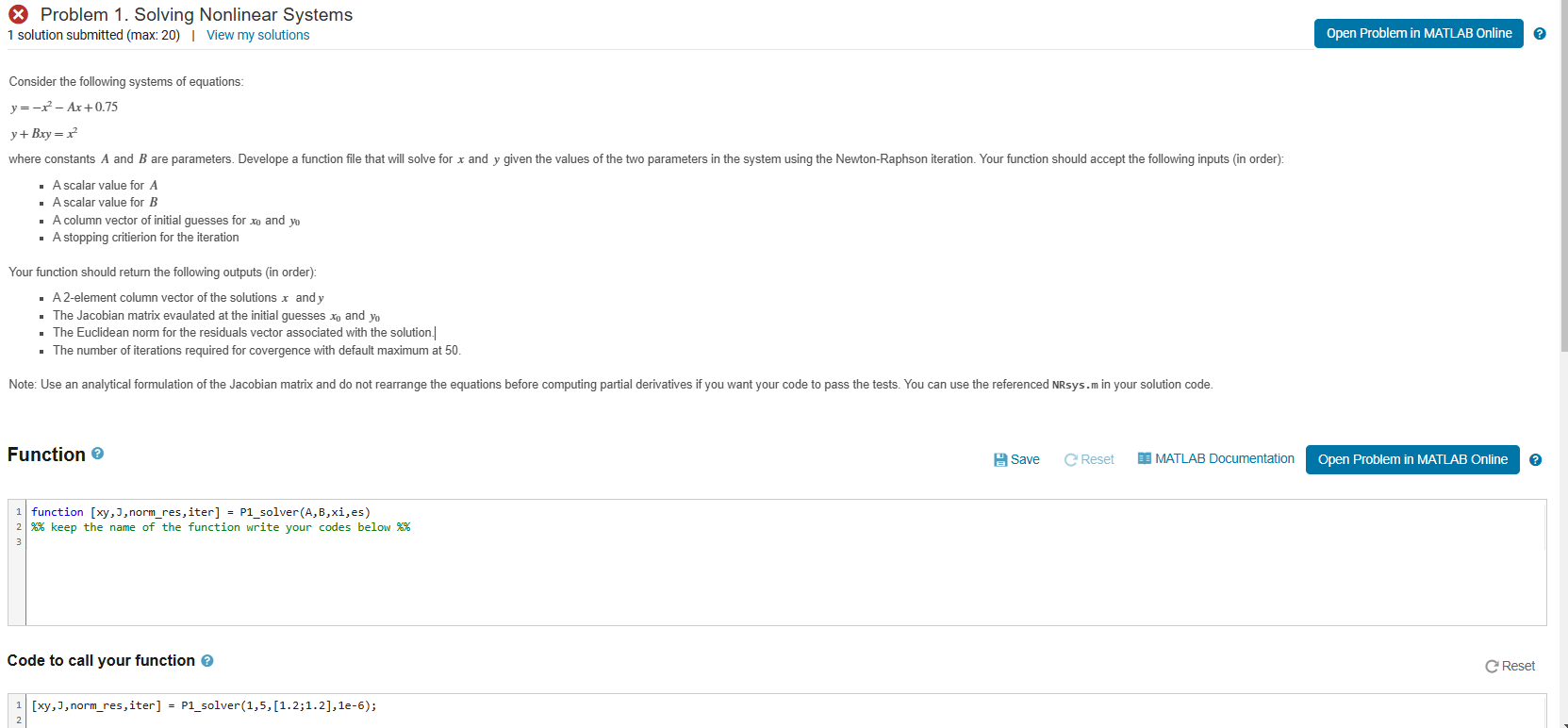
I am struggling figuring out why my code is encountering these issues

Consider the following systems of equations:

$y=-x^2-Ax+0\mathrm{.}75$

$y+Bxy=x^2$

where constants A and $B$ are parameters. Develope a function file that will solve for $x$ and $y$ given the values of the two parameters in the system using the Newton$-$Raphson iteration. Your function should accept the following inputs $($in order$)$:

Ascalar value for $A$

A scalar value for $B$

A column vector of initial guesses for $x_0$ and $y_0$

A stopping critierion for the iteration

Your function should return the following outputs $($in order$)$:

A $2-$element column vector of the solutions $x$ and $y$

The Jacobian matrix evaulated at the initial guesses $x_0$ and $y_0$

The Euclidean norm for the residuals vector associated with the solution.$|$

The number of iterations required for covergence with default maximum at $50.$

Note: Use an analytical formulation of the Jacobian matrix and do not rearrange the equations before computing partial derivatives if you want your code to pass the tests. You can use the referenced NRsys$.$m in your solution code.

Function $o.$

function $,$ norm$\_$res, iter$]=$ P$1\_$solver$(A,B,,$ es $)$

Here is my current code:

function $[$xy$,$ J$,$ norm$\_$res, iter$]=$ P$1\_$solver$($A$,$ B$,$ xi$,$ es$)$

$\%$ Initialize the Jacobian at current guess

J $=$ ones$(2,2)$;

J$(1,1)=-(2*$xi$(1))-$ A;

J$(1,2)=-1$;

J$(2,1)=(2*$xi$(1))-($B$*$xi$(2))$;

J$(2,2)=-1-($B$*$xi$(1))$;

$\%$ Define the system of equations

f $=$ @$($x$,$y$)-$x$^2-$ A$*$x $+0\mathrm{.}75-$ y;

g $=$ @$($x$,$y$)$ x$^2-$ y $-$ B$*$x$*$y;

max$\_$iter $=50$;

x$\_$old $=$ xi;

for iter $=1$:max$\_$iter

$\%$ Evaluate the function at current guess

F$\_$val $=[$f$($x$\_$old$(1),$ x$\_$old$(2))$; g$($x$\_$old$(1),$ x$\_$old$(2))]$;

$\%$ Update the Jacobian at current guess

J$(1,1)=-(2*$x$\_$old$(1))-$ A;

J$(1,2)=-1$;

J$(2,1)=(2*$x$\_$old$(1))-($B$*$x$\_$old$(2))$;

J$(2,2)=-1-($B$*$x$\_$old$(1))$;

$\%$ Compute update step using Newton$-$Raphson method

delta$\_$x $=-$J$\backslash$F$\_$val;

$\%$ Update estimate of root

x$\_$new $=$ x$\_$old $+$ delta$\_$x;

$\%$ Check convergence criterion $($Euclidean norm of residual vector$)$

norm$\_$res $=$ norm$($F$\_$val$)$;

if norm$\_$res $$ es $||$ all$($abs$($delta$\_$x$)$ es$*$abs$($x$\_$new$))$

break;

end

if iter $==$ max$\_$iter && norm$\_$res $>=$ es

warning$(\text{'}$Maximum iterations reached without achieving desired tolerance.$\text{'})$;

end

$\%$ Update initial guess for next iteration

x$\_$old $=$ x$\_$new;

end

xy $=$ x$\_$new;

end

Here are my current errors:

Assessment: $3$ of $5$ Tests Passed

Does the initial Jacobian matrix have the correct values for the example function inputs? $($Pretest$)$

Variable $J$ has an incorrect value.

Are the outputs correct for input values not given in the example?

Variable $J$ has an incorrect value.