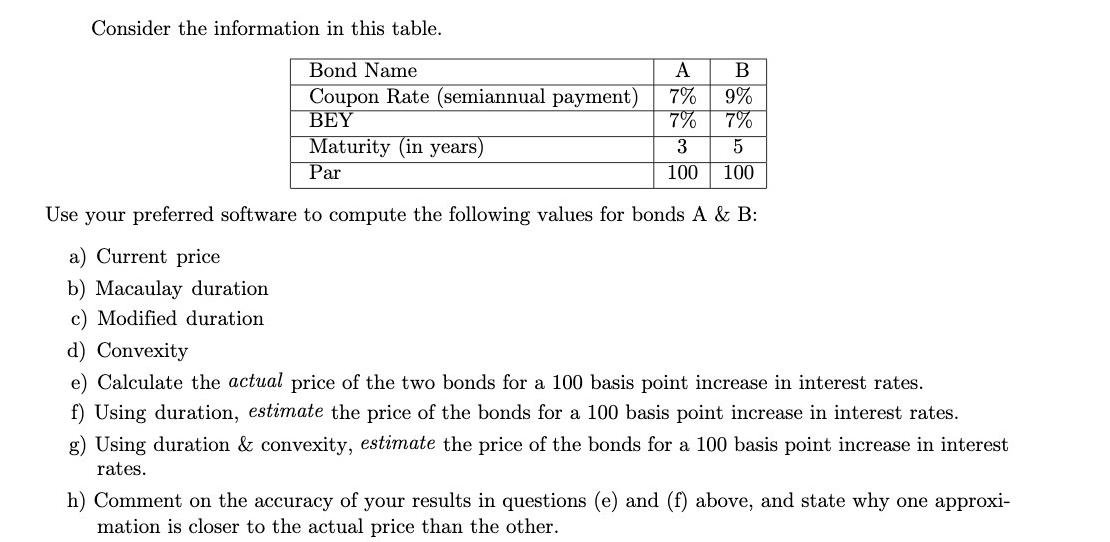
(i) Construct a portfolio of the two coupon bonds so that the future value of the portfolio is 1 million and the duration of this portfolio is equal to five years, assuming that the yield curve will remain flat at 10%. (ii) Show that if immediately after you purchased this portfolio the yield curve makes a permanent parallel downward or upward move of 1%, the future value of this portfolio at the end of year 5 will still be approximately 1 million. You have immunized the portfolio of the risk associated with parallel movements of the yield curve by buying a portfolio of coupon bonds so that the duration of the portfolio matches the number of years to the payment of the fixed liability. (iii) Suppose now that you have held your portfolio for one year after a 1% decrease in the yield curve to 9% which occurred immediately after you constructed your initial portfolio with a duration of five. There are now four years to the payment of the fixed liability. Use the money at your disposal (the market value of your investment at the end of year one) to construct a portfolio of coupon bonds with, duration equal to four years and a future value four years hence equal to approximately 1 million, given the new flat yield curve at 9%. Show that if the yield curve then makes a parallel upward or downward move of 1%, the future value of your portfolio four years from now will be unchanged. You have approximately funded your liability of 1 million at the end of the fifth year. (Compare the difference between the future value of your portfolio and your fixed liability here and in part b).) This technique is called "duration matching": if you adjust your portfolio over time so that its duration always matches the years to the payment date of your fixed liabilities, you will approximately immunize the risk of parallel shifts in the yield curve. Consider the information in this table. A B 7% 9% 7% 7% 3 5 100 100 Use your preferred software to compute the following values for bonds A & B: a) Current price b) Macaulay duration c) Modified duration Bond Name Coupon Rate (semiannual payment) BEY Maturity (in years) Par d) Convexity e) Calculate the actual price of the two bonds for a 100 basis point increase in interest rates. f) Using duration, estimate the price of the bonds for a 100 basis point increase in interest rates. g) Using duration & convexity, estimate the price of the bonds for a 100 basis point increase in interest rates. h) Comment on the accuracy of your results in questions (e) and (f) above, and state why one approxi- mation is closer to the actual price than the other. You want to immunize a single payment liability of $1331 that comes due in three years. To do this, you will use a portfolio composed of the following bonds: A. a four-year pure discount bond with a price of $1000 for a face value of $1464.10. B. a two-year 10% coupon bond with annual payments, selling at par. [Calculate yields as effective annual rates, and do the calculations on an annual basis.]