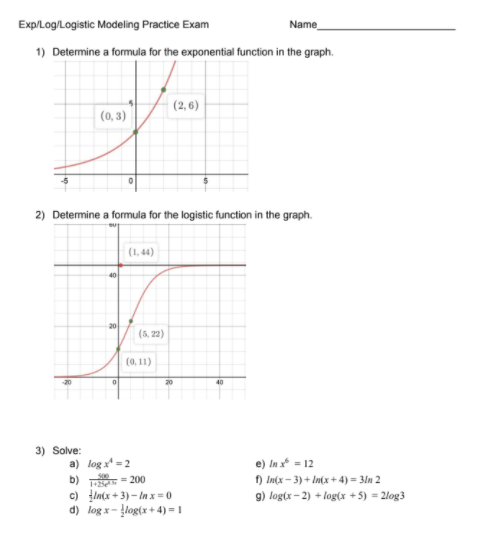
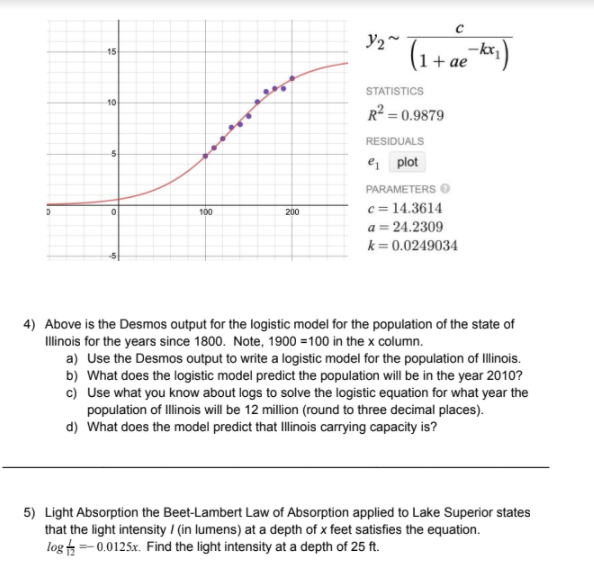
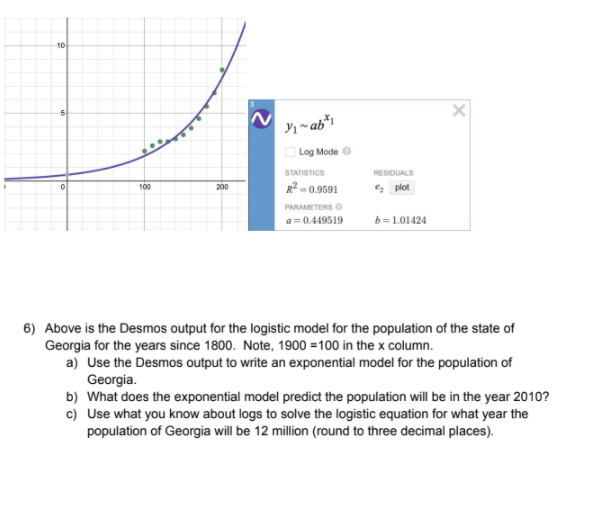
I had COVID and was quarantined for two weeks from school and missed an entire unit for math. My teacher has been very little help and I'm trying the best that I can to get caught up because I have to take the test for this unit in a couple of days and I'm very nervous. I have attached screenshots of the practice test (he doesn't grade them), but if you could help me understand how to do what's on this practice test, I might be able to do okay on the test. (I have been taught practically nothing while I've been quarantined). Thank you, I really appreciate any help!

Walking me through/explaining how to do them is my biggest request because I'm genuinely trying to learn how to do this :)

Exp/Log/Logistic Modeling Practice Exam Name 1) Determine a formula for the exponential function in the graph. (2, 6) (0, 3) 2) Determine a formula for the logistic function in the graph. (1, 44) (5. 22) (0, 11) 3) Solve: a) logx = 2 e) In x = 12 b) HI = 200 () In(x - 3) + (x +4) = 3/m 2 c) /m(x+ 3)-Max=0 9) log(x - 2) + log(x +5) = 2log3 d) log x - !log(r+ 4) = 1C 15 (1 + ae kox, ) STATISTICS 10 R- = 0.9879 RESIDUALS 5 e plot PARAMETERS 100 200 c = 14.3614 a = 24.2309 k = 0.0249034 4) Above is the Desmos output for the logistic model for the population of the state of Illinois for the years since 1800. Note, 1900 =100 in the x column. a) Use the Desmos output to write a logistic model for the population of Illinois. b) What does the logistic model predict the population will be in the year 2010? c) Use what you know about logs to solve the logistic equation for what year the population of Illinois will be 12 million (round to three decimal places). d) What does the model predict that Illinois carrying capacity is? 5) Light Absorption the Beet-Lambert Law of Absorption applied to Lake Superior states that the light intensity / (in lumens) at a depth of x feet satisfies the equation. log =-0.0125x. Find the light intensity at a depth of 25 ft.10 5 N X 1 - ab 1 Log Mode STATISTICS RESIDUALS 100 200 R2- 0.9591 plot PARAMETERS O 0 =0.449519 b =1.01424 6) Above is the Desmos output for the logistic model for the population of the state of Georgia for the years since 1800. Note, 1900 =100 in the x column. a) Use the Desmos output to write an exponential model for the population of Georgia. b) What does the exponential model predict the population will be in the year 2010? c) Use what you know about logs to solve the logistic equation for what year the population of Georgia will be 12 million (round to three decimal places)