I have 11 question Homework for calc 1

I upload a pic of question

Please I need the answers asap.

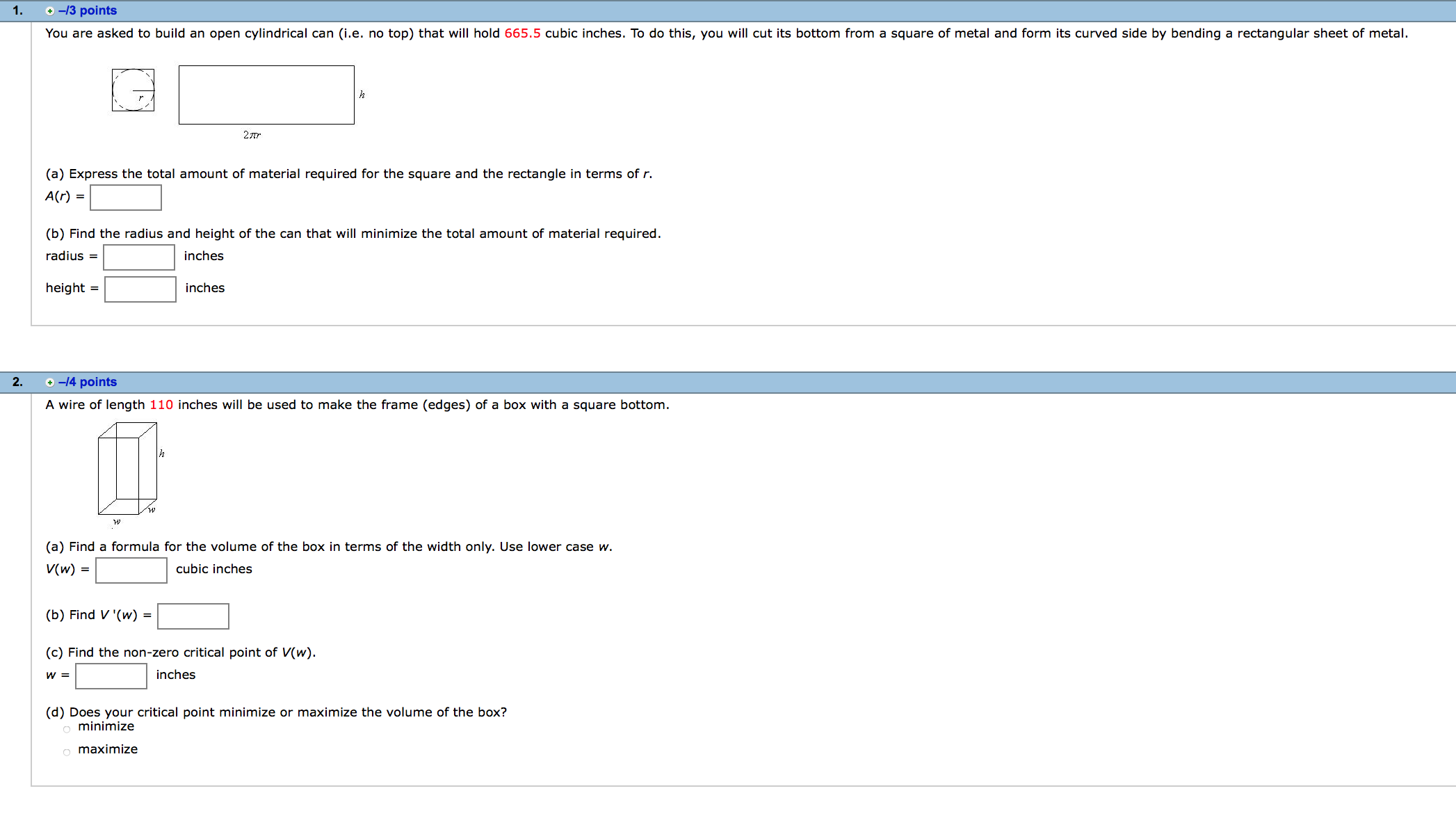
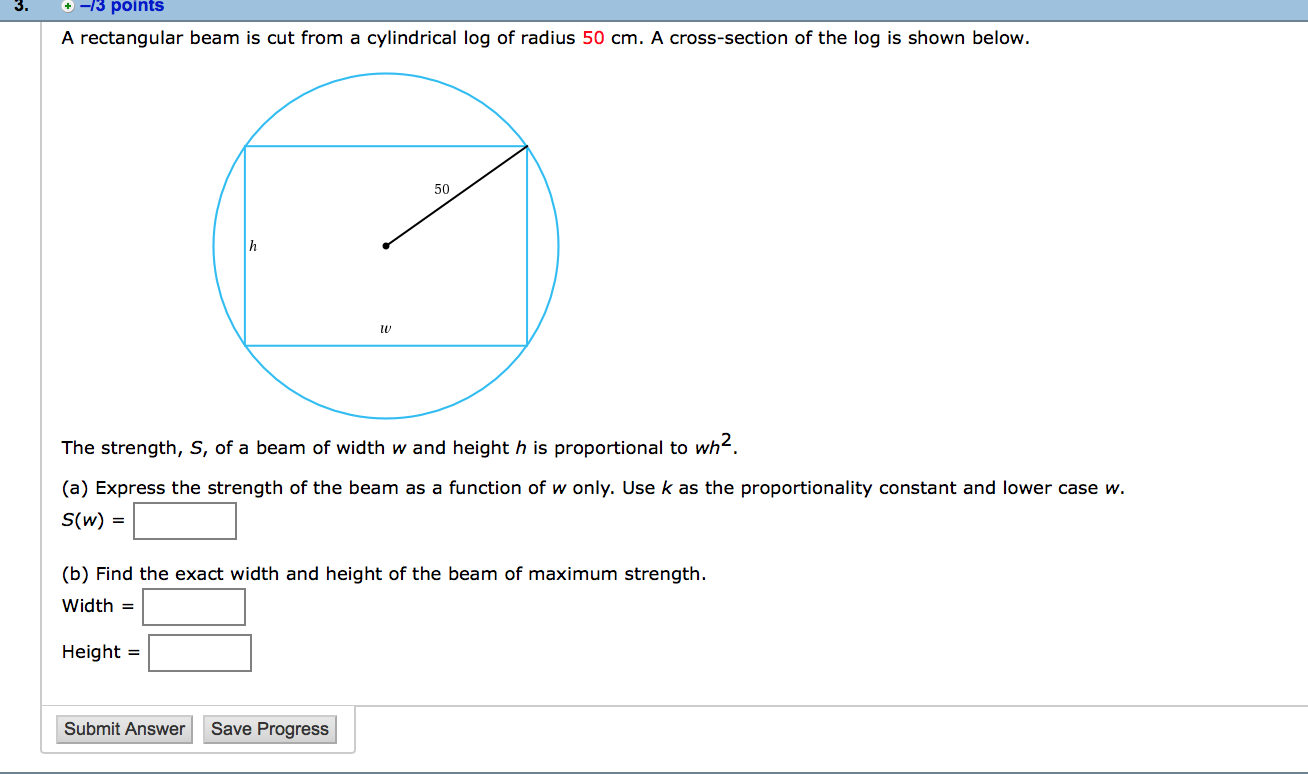
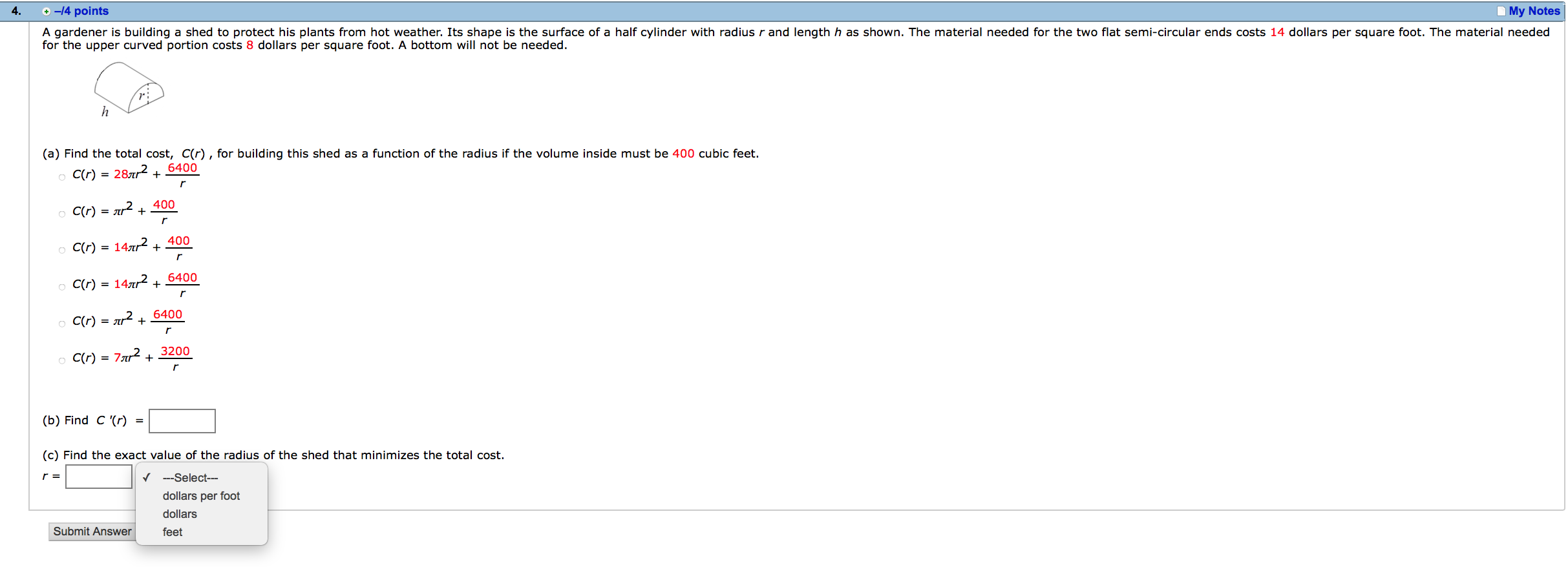
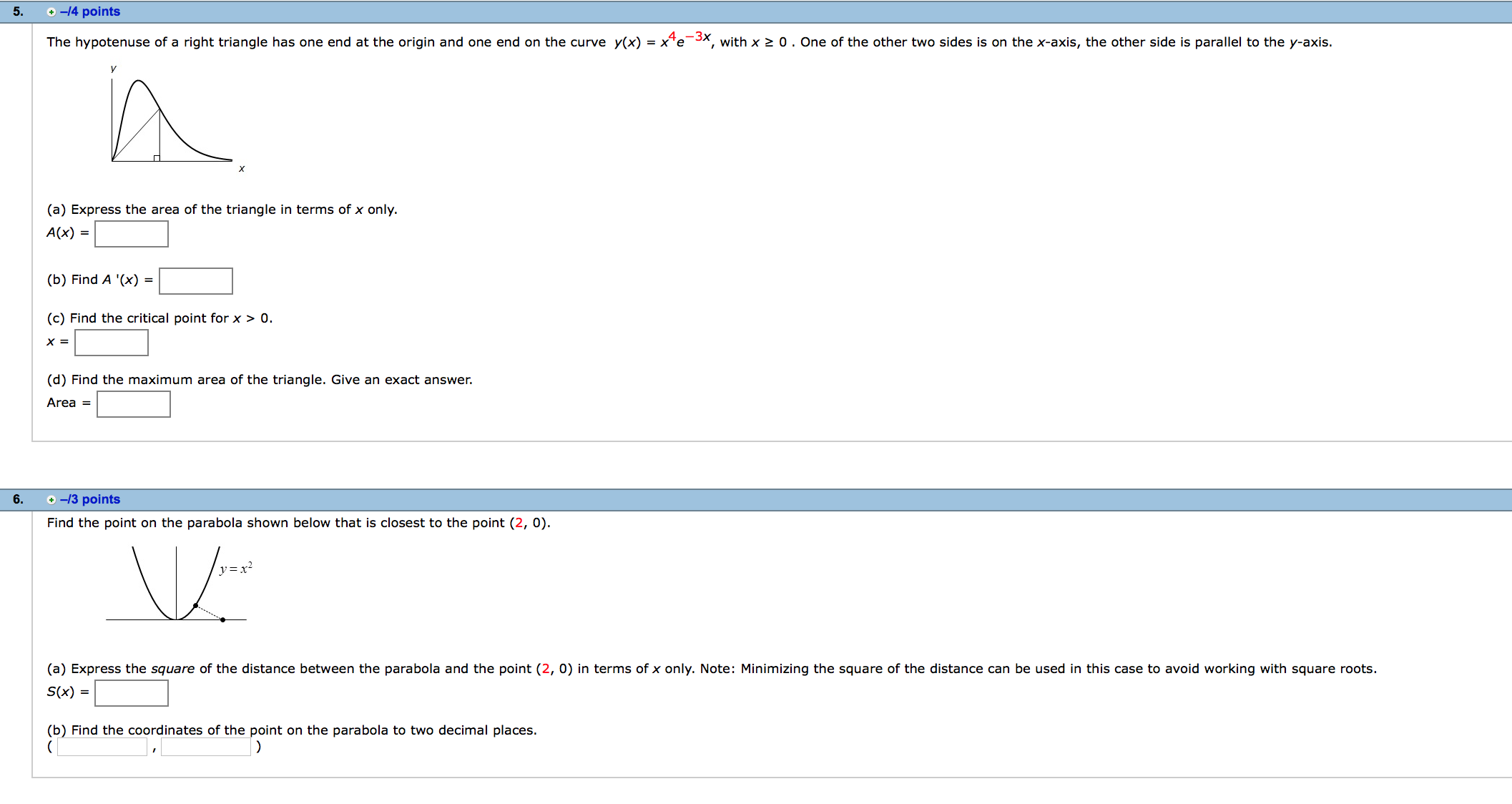
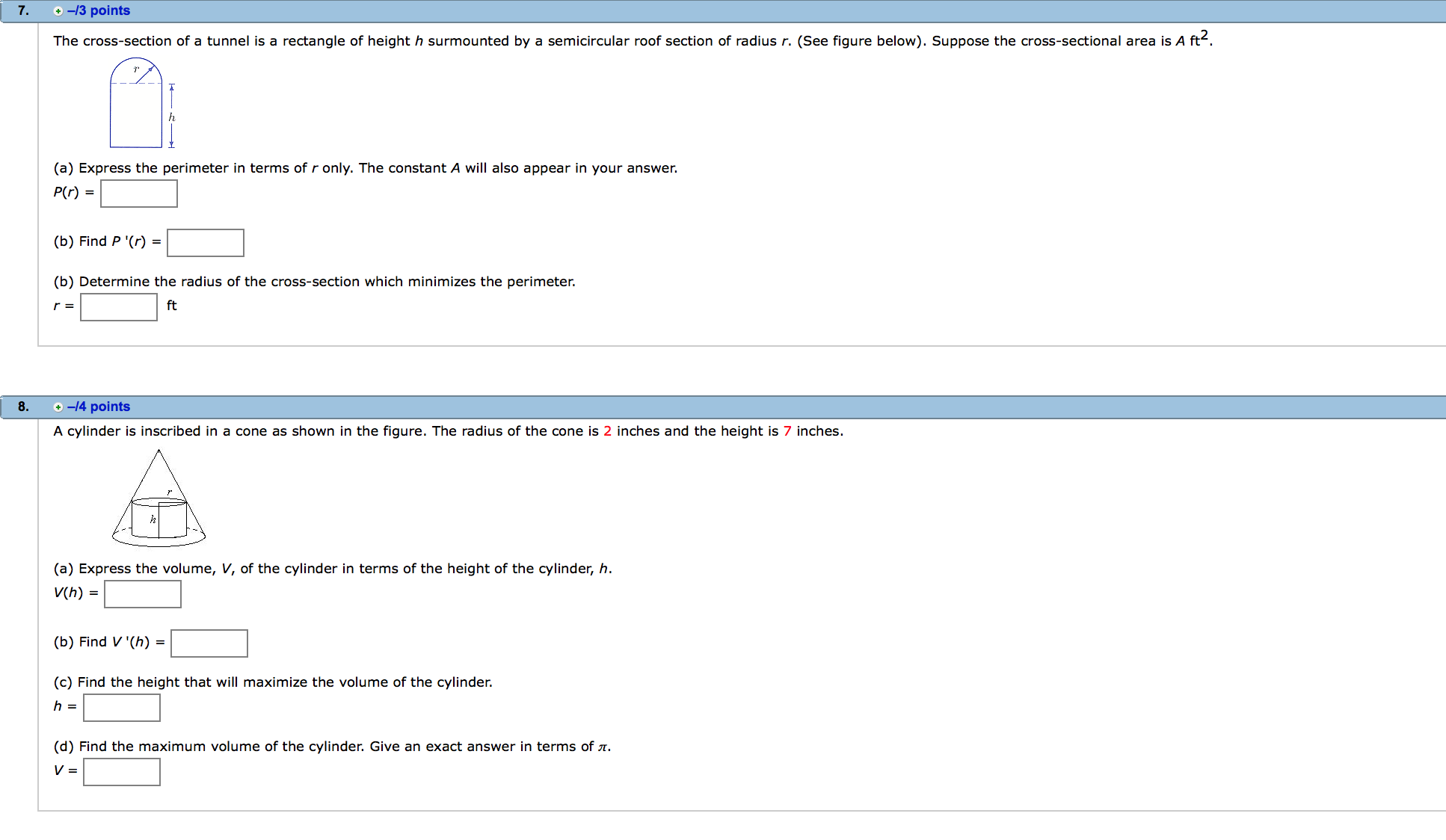
You are asked to build an open cylindrical can (i.e. no top) that will hold 665.5 cubic inches. To do this, you will cut its bottom From a square of metal and form is curved side by bending a rectangular sheet of metal. 27!? (a) Express the total amount of material required for the square and the rectangle in terms of r. 40') = (b) Find the radius and height of the can that will minimize the total amount of material required. radius = inches height = inches A wire of length 110 inches will be used to make the frame (edges) of a box with a square bottom. w (a) Find a formula for the volume of the box in terms of the width only. Use lower case w. V(w) = cubic inches (b) Find V'(w) = (c) Find the non-zero critical point of V(w). (d) Does your critical point minimize or maximize the volume of the box? 0 minimize o maximize A rectangular beam is cut from a cylindrical log of radius 50 cm. A cross-section of the log is shown below. 50 The strength, 5, of a beam of width w and height h is proportional to wh2. (a) Express the strength of the beam as a function of w only. Use k as the proportionality constant and lower case w. (b) Find the exact width and height of the beam of maximum strength. A gardener is building a shed to protect his plants from hot weather. 15 shape is the surface of a half cylinder with radius r and length h as shown. The material needed (or the two at semi-circular ends oasis 14 dollars per square foot. The material needed for the upper curved portion costs 8 dollars per square font. A bottom will not be needed. ,, P (a) Find the total cost, C(r) , for building this shed as a funcan of the radius if the volume Inside must be 400 cubic feet. n C(r) = 28.112 + 54"\" h C(r) = m2 + g n C(r) = mm2 + g ,. C(r) = 1m? + \"I?\" n C(r) = :02 + g n C(r) = 7m2 + 320 r (b) Find c '(r) = (c) Find the exact value of the radius 0f the shed that minimizes the total cost. r= I sma dallars per loot duller: led! The hypotenuse of a right triangle has one end at the origin and one end on the curve y(x) = x4e_3x, with x 2 0 . One of the other two sides is on the x-axis, the other side is parallel to the y-axis. V (a) Express the area of the triangle in terms ofx only. '0') = (b) Find A '(x) = (c) Find the critiml point forx > 0. x= (d) Find the maximum area of the triangle. Give an exact answer. Area = Find the point on the parabola shown below that is closest to the point (2, 0). (a) Express the square of the distance between the parabola and the point (2, 0) in terms ofx only. Note: Minimizing the square of the distance can be used in this case to avoid working with square roots. (b Find the coordinata of the oint on the parabola to two decimal places. ( I ) The cross-section of a tunnel is a rectangle of height h surmounted by a semicircular roof section of radius r. (See figure below). Suppose the cross-sectional area is A ftz. (a) Express the perimeter in terms of r only. The constantA will also appear in your answer. (b) Find P '(r) = |:| (b) Determine the radius of the cross-section which minimizes the perimeter. r=:|ft A cylinder is inscribed in a cone as shown in the gure. The radius of the cone is 2 inches and the height is 7 incha. a (a) Express the volume, V, of the cylinder in terms of the height of the cylinder, h. (b) Find V'(h) = |:| (c) Find the height that will maximize the volume of the cylinder. h = (d) Find the maximum volume of the cylinder. Give an exact answer in terms of :1. V = A rectangular swimming pool is to be built with an area of 3200 square feet. The owner wants 5-foot wide decks along either side and 10-foot wide decks at the two ends. In this problem you will nd the dimensions of the smallest piece of property on which t. (a) If the dimensions of the swimming pool are denoted by x and y, which of the following functions mould be used to represent the area of the pleoe of property needed? .. A(x) = (323 + 5)(x + m) n A(x) = (% 1o)(x 20) ,. A(x) = (m + 10)(x + 20) x n A(x) = (320" + 1o)(32 + 20) X X n A(X) = (% 5)(x 10) (b) What are the dimensions of the smallest piece of property on which the pool can be built? shorter side R longer slde ft A landscape architect plans to enclose a 1800 square foot rectangular region In a botanical garden. She WI\" use shrubs costing $25 per foot along three sides and fencmg costing $10 per foot along the north side. fence me: y shrub: x shrubs (a) Ifx Is the length of fencing used, write a formula for the total 005: In berms dfx only. C(x) = (b) Find the length of fence that will minimize the total cost. Give an exact answer. x = feet (c Find the minimum total cost. Give your answer to the nearest penny $ To get the best view (If the Statue af Liberty, you should be at the positian where 6 is a maximum. Suppose the statue stands 100 meters high, including the pedestal, which is 50 meters high. (a) We can write 0 = B a. Let d be your distance from the base of the statue. Express [3 in terms of d. 13(4) = Now express 9 in terms (11' d. 9(d) = (b) Find 9'01) = (c) How far from the base shuuld you be? Give an exact