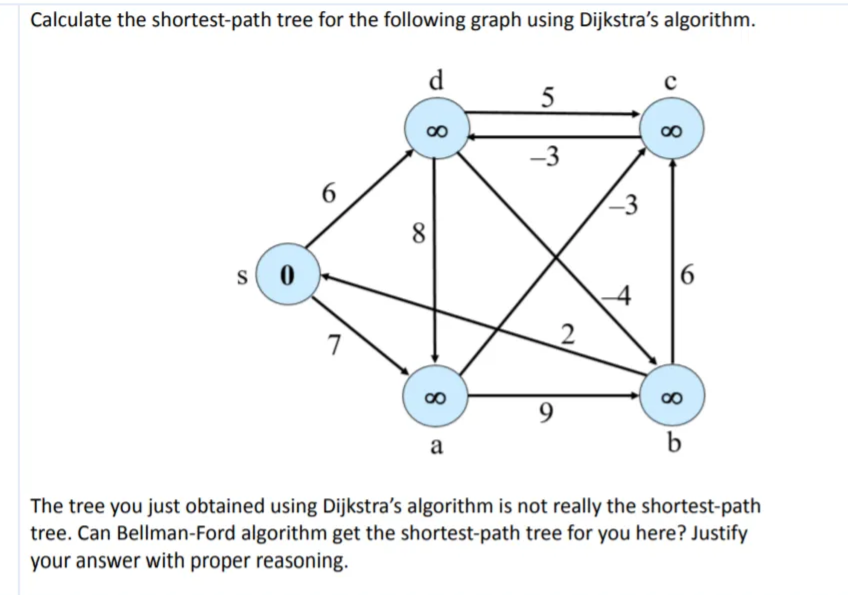
I have attached psudocode for Dijkstra algorithm and bellman ford algorithm

Calculate the shortest-path tree for the following graph using Dijkstra's algorithm. d 5 -3 6 -3 8 s 6 7 2 8 9 a b The tree you just obtained using Dijkstra's algorithm is not really the shortest-path tree. Can Bellman-Ford algorithm get the shortest-path tree for you here? Justify your answer with proper reasoning. Bellman-Ford Algorithm Bellmanford (). for each v EV d[v] = 0; d[s] = 0; Initialize d[l, which will converge to shortest-path values for i=1 to VI-1 for each edge (u, v) E E Relax(u,v,w); Relaxation: Make V-1 passes, relaxing each edge for each edge (u,v) E E if (d[v] > d[u] + w(u, v)) return "no solution"; Test for solution Under what condition do we get a solution? Relax (u,v,w): if (d[v] > d[u] +w(u, v)) then d[v]=d[u] +w (u, v) p[v]=u Activate Wine Dijkstra's Algorithm Dijkstra (G) for each v EV d[v] d[s] = 0; s = ; Q = V; = 0; while (Q + ) u = ExtractMin (Q); S = SU {u}; for each ve u->Adj[] if (d[v] > d[u] +w (u, v) ) Note: this d[v] d[u]+w (u, v); is really a p[v] = u; call to Q->DecreaseKey0 = Relaxation Step