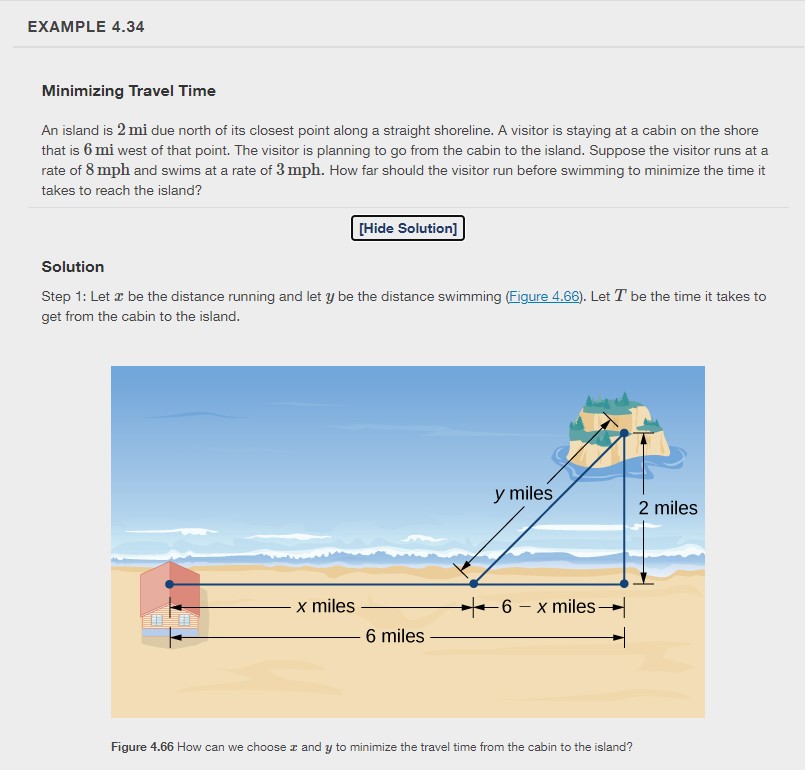
I have posted example 4.34 below, but I need help with part 2. Part 1 is given for context.

Part I: Complete the following steps: 1. Read Example 4.34 in Section 4.7 of Calculus, Volume 1. 2. Consider the following scenario: A lifeguard is at point A of a circular pool with diameter 40 m. He must reach someone who is drowning on the exact opposite side of the pool, at position C. The lifeguard swims with a speed v = 3 m/s from point A to point B, and then runs around the pool from point B to point C at speed w = 9 m/s. B A C 3. Find a function that measures the total amount of time it takes to reach the drowning person as a function of the swim angle, 0 expressed in radians. 4. Find at what angle 0, in radians, the lifeguard should swim to reach the drowning person in the least amount of time. 5. What is the domain of the function you created in part (a)? Part II: Based on your work in Part I, discuss the following: 1. How do you know that the function you created in Part I has a maximum and minimum value? 2. Discuss how your answers to Part I would be affected if the diameter of the pool increased. 3. For what running speed would it be faster to swim the entire time? What angle would correspond to this scenario? 4. For what angle would it take the longest to reach the drowning person? 5. Suppose the pool was rectangular. Respond to the following: a. Does it still make sense to parameterize using 0? Why or why not? i. If not, what parameter would you use? ii. If so, how does the parameterization change? b. Set up, but do not solve, this problem with a rectangular pool. 6. Answer the following questions that reference Example 4.34: a. How do we know that the function T(x) has a maximum and minimum? b. What restrictions are there on what the domain of T can be in this scenario? c. Elaborate, in your own words, on why we must evaluate T(0) and T(6).EXAMPLE 4.34 Minimizing Travel Time An island is 2 mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is 6 mi west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of 8 mph and swims at a rate of 3 mph. How far should the visitor run before swimming to minimize the time it takes to reach the island? [Hide Solution] Solution Step 1: Let c be the distance running and let y be the distance swimming (Figure 4.66). Let T be the time it takes to get from the cabin to the island. y miles 2 miles x miles 6 - x miles- 6 miles Figure 4.66 How can we choose c and y to minimize the travel time from the cabin to the island