
I have some questions that I did not figure it out in the topic "Confidence intervals 1 sample means". Please help me, thank you so much!!!
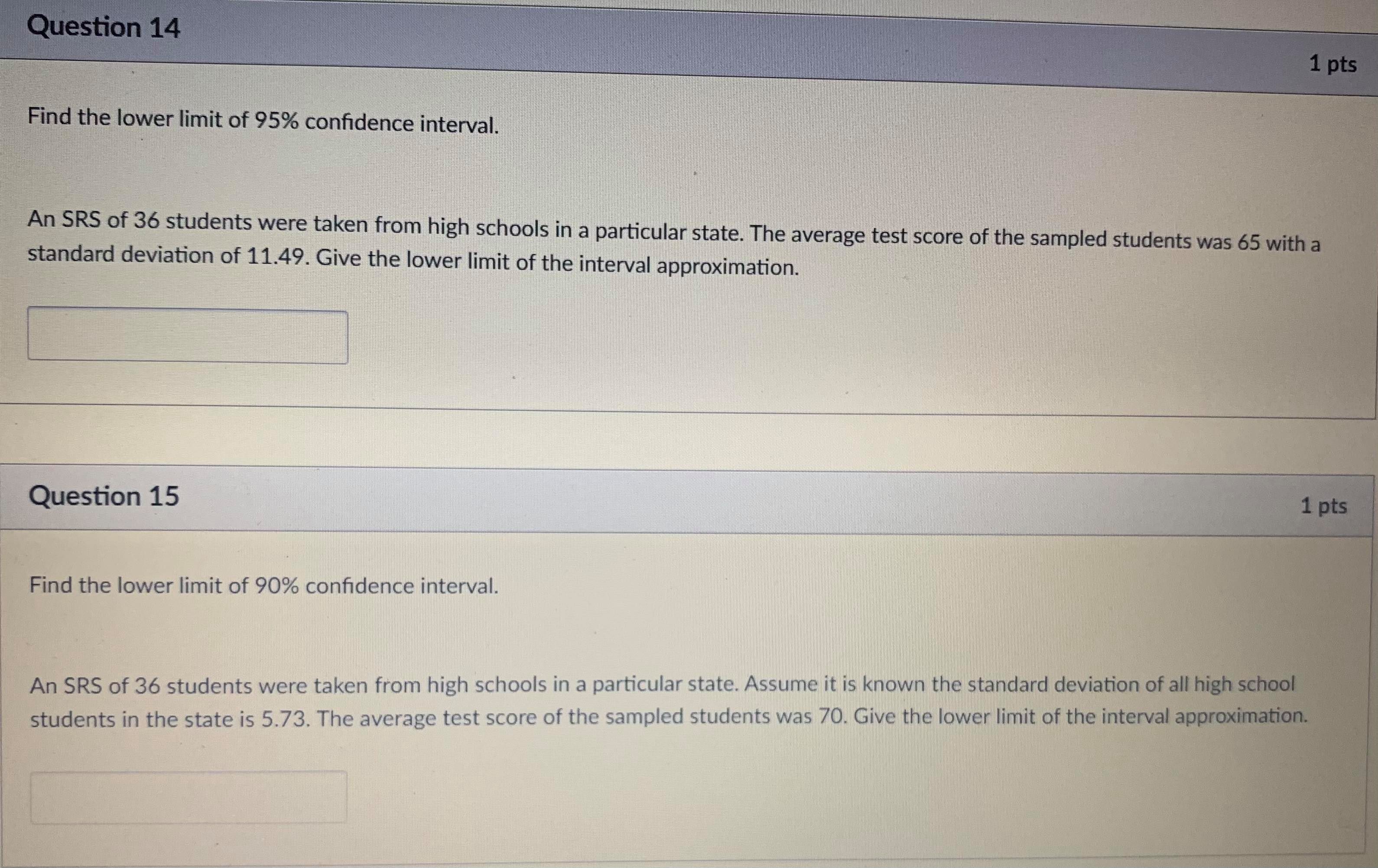
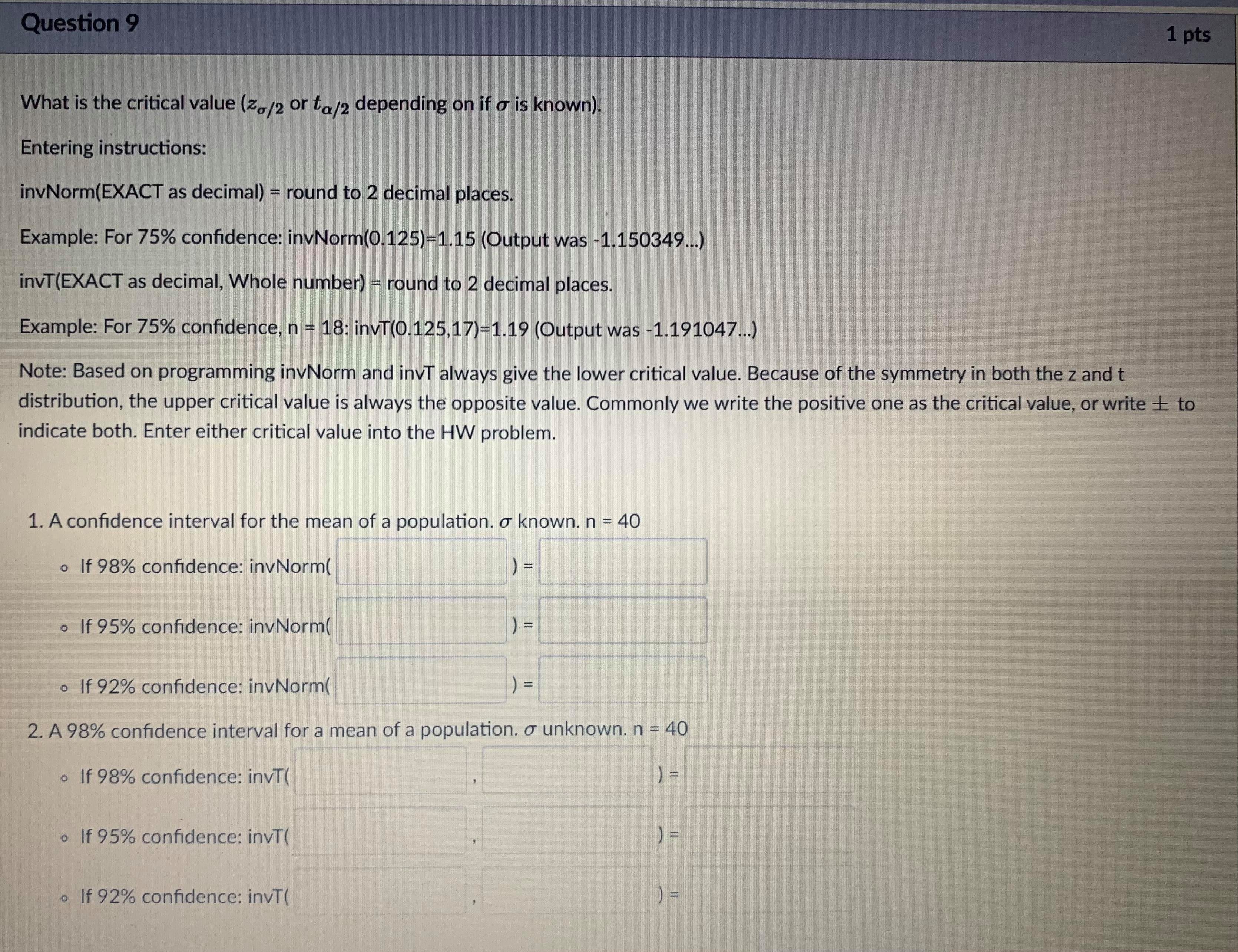
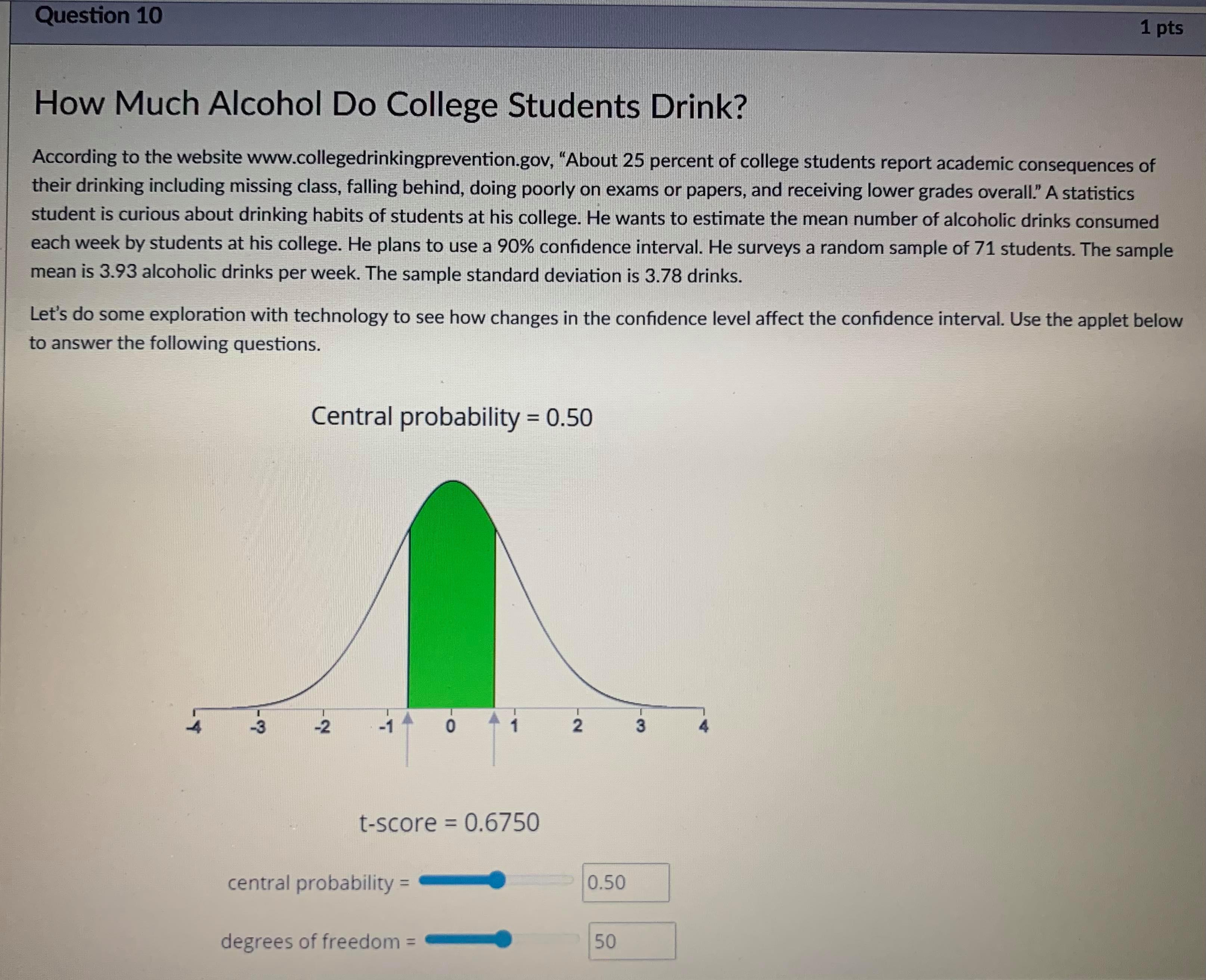
Question 11 1 pts How Much Alcohol Do College Students Drink? According to the website www.collegedrinkingprevention.gov, "About 25 percent of college students report academic consequences of their drinking including missing class, falling behind, doing poorly on exams or papers, and receiving lower grades overall." A statistics student is curious about drinking habits of students at his college. He wants to estimate the mean number of alcoholic drinks consumed each week by students at his college. He plans to use a 90% confidence interval. He surveys a random sample of 71 students. The sample mean is 3.93 alcoholic drinks per week. The sample standard deviation is 3.78 drinks. Let's do some exploration with technology to see how changes in the confidence level affect the confidence interval. Use the applet below to answer the following questions. Central probability = 0.50 -3 -2 -1 0 2 t-score = 0.6750 central probability = 0.50 degrees of freedom = 50central probability = 0.5 degrees of freedom = 50 Answer the following question about this study. Use the applet above, if necessary. Find the critical T-value for this 90% confidence interval. Hint: Use the applet to find the T-value for 90% confidence with df = 71 - 1 = 70. G ( 0 words >Question 14 1 pts Find the lower limit of 95% confidence interval. An SRS of 36 students were taken from high schools in a particular state. The average test score of the sampled students was 65 with a standard deviation of 11.49. Give the lower limit of the interval approximation. Question 15 1 pts Find the lower limit of 90% confidence interval. An SRS of 36 students were taken from high schools in a particular state. Assume it is known the standard deviation of all high school students in the state is 5.73. The average test score of the sampled students was 70. Give the lower limit of the interval approximation.Question 9 1 pts What is the critical value (Zo/2 or ta/2 depending on if a is known). Entering instructions: invNorm(EXACT as decimal) = round to 2 decimal places. Example: For 75% confidence: invNorm(0.125)=1.15 (Output was -1.150349...) invT(EXACT as decimal, Whole number) = round to 2 decimal places. Example: For 75% confidence, n = 18: invT(0.125,17)=1.19 (Output was -1.191047...) Note: Based on programming invNorm and invT always give the lower critical value. Because of the symmetry in both the z and t distribution, the upper critical value is always the opposite value. Commonly we write the positive one as the critical value, or write + to indicate both. Enter either critical value into the HW problem. 1. A confidence interval for the mean of a population. o known. n = 40 . If 98% confidence: invNorm( . If 95% confidence: invNorm( . If 92% confidence: invNorm( 2. A 98% confidence interval for a mean of a population. o unknown. n = 40 . If 98% confidence: invT( . If 95% confidence: invT( . If 92% confidence: invT(Question 10 1 pts How Much Alcohol Do College Students Drink? According to the website www.collegedrinkingprevention.gov, "About 25 percent of college students report academic consequences of their drinking including missing class, falling behind, doing poorly on exams or papers, and receiving lower grades overall." A statistics student is curious about drinking habits of students at his college. He wants to estimate the mean number of alcoholic drinks consumed each week by students at his college. He plans to use a 90% confidence interval. He surveys a random sample of 71 students. The sample mean is 3.93 alcoholic drinks per week. The sample standard deviation is 3.78 drinks. Let's do some exploration with technology to see how changes in the confidence level affect the confidence interval. Use the applet below to answer the following questions. Central probability = 0.50 - 3 -2 0 2 t-score = 0.6750 central probability = 0.50 degrees of freedom = 50-2 2 t-score = 0.6750 central probability = 0.50 degrees of freedom = 50 Answer the following question about this study. Use the applet above, if necessary. Which of the following is an appropriate conclusion we can draw from this confidence interval? We are 90% confident that the mean number of alcoholic drinks consumed by all students at this college during the previous week is between 3.18 and 4.68. We are 90% confident that each student at this school consumed between 3.18 and 4.68 alcoholic drinks in the previous week. We expect 90% of all students on the campus to have consumed between 3.18 and 4.68 alcoholic drinks in the previous week. We are 90% confident that the mean number of alcoholic drinks consumed by all college students in the U.S. during the previous week is between 3.18 and 4.68
















